Search results

Create the page "Tetration to real base" on this wiki! See also the search results found.

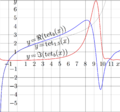
• File:Shelr80.png Explicit plot of [[tetration to Sheldon base]] for real values of the argument. For comparison, the black line shows the graphic for real base $b=1.5$, id est, $y=\mathrm{tet}_{1.5}(x)$ (1,563 × 1,454 (237 KB)) - 08:51, 1 December 2018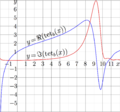

• File:Shelre60.png Explicit plot of [[tetration to Sheldon base]] for real values of the argument. should be loaded in order to compile the code below: (1,172 × 1,090 (142 KB)) - 08:51, 1 December 2018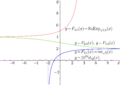

• File:Sqrt2sufuplot.png Four superexponentials to base \(b=\sqrt{2}\) They are real-holomorphic solutions \(F\) of the transfer equation (3,520 × 2,507 (408 KB)) - 10:11, 10 June 2022

• File:Tet5loplot.jpg Graphical search for the real [[fixed point]]s of [[tetration]]: $\mathrm e\!=\!\exp(1)\!\approx\!2.71$ is base of the natural logarithm, (1,477 × 1,486 (283 KB)) - 08:53, 1 December 2018

• File:TetsheldonmapT600.jpg [[Complex map]] of [[Tetration]] to the [[Sheldon base]] $b= 1.52598338517 + 0.0178411853321\, \mathrm i$. Constants $L_1$ and $L_2$ are [[fixed point]]s of logarithm to base $b$; they are determined (and evaluated) through function [[filog]]: (5,130 × 1,776 (1.02 MB)) - 08:54, 1 December 2018

• Ackermann function
  ...no commonly accepted system of notations is established, at the reference to the Ackermann function, either the definition, or, at least, link should be ...ann function]]. Beeng written with capital, Ackermann, this word may refer to famous scientist [[Wilhelm Ackermann]]<ref>https://en.wikipedia.org/wiki/Wi
  10 KB (1,534 words) - 06:44, 20 July 2020
• Base e1e
  [[Base e1e]] refers to the value of base \(b= \eta =\exp(1/\mathrm e)\approx 1.4446678610\) ...corresponding [[exponential]], [[SuperExponential]] (in particular, the [[tetration]]) and the inverse functions.
  4 KB (559 words) - 17:10, 10 August 2020
• Base sqrt2
  [[File:ExpQ2mapT.png|300px|thumb|[[Complex map|Map]] of [[exponent]] to base \(b=\sqrt{2}\); lines of constant \(u\) and lines of constant \(v\) show [[File:Logq2mapT1000.jpg|300px|thumb|[[Complex map|Map]] of [[Logarithm]] to base \(b=\sqrt{2}\); lines of constant \(u\) and lines of constant \(v\) show
  3 KB (557 words) - 18:46, 30 July 2019
• Pentation
  ...n]] of [[tetration]], constructed with [[regular iteration]] at its lowest real fixed point. ...\(\mathrm e=\exp(1)\approx 2.71\), then the tetration is called [[natural tetration]] and the corresponding pentation is called [[Natural pentation]].
  5 KB (803 words) - 18:48, 30 July 2019
• Special function
  ...s the way of evaluation of the function. In the most of cases, this refers to a [[holomorphic function]] of a single complex variable. 2. Alternative representations of the function, relation of the function to other elementary functions or with other special functions, defined earlier
  7 KB (991 words) - 18:48, 30 July 2019
• Nemtsov function and its iterates
  ...ion, prepared for publication, with goal to check the cross-references and to catch misprints, if any. In 1950, the interest to the non-integer iterates had been boiled-up with iterates of exponential an
  15 KB (2,392 words) - 11:05, 20 July 2020
• Shell-Thron region
  [[William Harold Paulsen]]. Tetration for complex bases. ...aper determined conditions for a unique solution the case where \( b \) is real and \(b>e^{1/e}\).
  7 KB (1,082 words) - 07:03, 13 July 2020

• File:ShellThronRegionPaulsen2.png [[William Harold Paulsen]]. Tetration for complex bases. ...aper determined conditions for a unique solution the case where \( b \) is real and \(b>e^{1/e}\). (569 × 580 (16 KB)) - 06:51, 13 July 2020

• Tet2Li3.cin
  ...ntation of approximation of [[tetration to base 2]] for moderate values of real part of argument and positive moderated values of the imaginary part of the #define Re(x) x.real()
  7 KB (724 words) - 14:58, 28 July 2020
• Tetration to base 2
  ...{tet}_2\) ) is special case of [[Tetration]] \(\mathrm {tet}_b\) while the base \( b\!=\!2\). ...real values of argument, [[tetration to base 2]] is compared to tetrations to other bases in Fig.1.
  6 KB (845 words) - 17:10, 23 August 2020
• Theorem on increment of tetration
  Fig.1. Asymptoric parameters of [[Tetration]] versus \(\beta\) [[Theorem on increment of tetration]] is statement about asymptotic behavior of solution of the [[Transfer equa
  4 KB (548 words) - 14:27, 12 August 2020

• File:TetKK200.png ...tic behavior of [[Tetration]] to real base \(b\), versus logarithm of this base, \( \beta=\ln(b)\). Values correspond to the upped half of the complex plane; so, \(\Im(L)\ge 0\). Curve for \(L^*\) (897 × 1,279 (29 KB)) - 12:45, 12 August 2020

• Sledgehammer to crack a nut
  ...ut]] may refer to application of a strong, powerful, complicated formalism to a task that does not worth such an effort. [[Sledgehammer to crack a nut]] may refer to using a very powerful instrument or weapon, applying much more efforts, for
  5 KB (712 words) - 08:18, 9 May 2024

View (previous 20 | next 20) (20 | 50 | 100 | 250 | 500)