File:Exp1mapT200.jpg
Original file (2,281 × 1,179 pixels, file size: 1.14 MB, MIME type: image/jpeg)
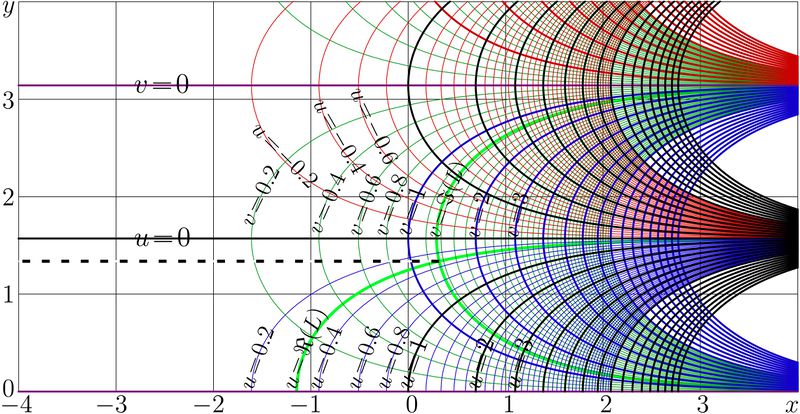
Complex map of the first iteration of exponent in the upper half-plane,
$u+\mathrm i v = \mathrm{tet}(1.+\mathrm{ate}(z))=\exp(z)$ in the $z=x+\mathrm i y$ plane.
The additional thick green lines show $u=\Re(L)$ and $v=\Im(L)$ where $L\approx 0.3+1.3 \mathrm i $ is fixed point of logarithm, $L=\ln(L)$.
The generator below, that plots this image, uses representation of the exponential through tetration and arctetration. WIth minimal modification, this code can generate the similar picture for any other iterate of the exponential, even non-integer and eve nomplex iterate.
C++ generator of curves
// Files ado.cin, conto.cin, fsexp.cin and fslog.cin should be loaded in the working directory in order to compile the code below.
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include<complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"
#include "fsexp.cin"
#include "fslog.cin"
main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
int M=401,M1=M+1;
int N=403,N1=N+1;
DB X[M1],Y[N1];
DB *g, *f, *w; // w is working array.
g=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
f=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
w=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
char v[M1*N1]; // v is working array
FILE *o;o=fopen("exp1map.eps","w"); ado(o,802,402);
fprintf(o,"401 1 translate\n 100 100 scale\n");
fprintf(o,"1 setlinejoin 2 setlinecap\n");
DO(m,M1) X[m]=-4+.02*(m-.5);
DO(n,N1) { y=0.+.01*(n-.5); if(y>Im(Zo)) break; Y[n]=y; }
Y[n] =Im(Zo)-.00001;
Y[n+1]=Im(Zo)+.00001;
for(m=n+2;m<N1;m++) Y[m]=.01*(m-2-.5);
for(m=-4;m<5;m++){M(m,0) L(m,4) }
for(n=0;n<5;n++){M( -4,n) L(4,n)}
fprintf(o,".006 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){ g[m*N1+n]=999; f[m*N1+n]=999;}
DO(m,M1){x=X[m]; if(m/10*10==m) printf("x=%6.3f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y); //if(abs(z+2.)>.019)
c=FSEXP(1.+FSLOG(z));
p=Re(c); q=Im(c);// if(p>-19 && p<19 && ( x<2. || fabs(q)>1.e-12 && fabs(p)>1.e-12) )
{ g[m*N1+n]=p;f[m*N1+n]=q;}
}}
fprintf(o,"1 setlinejoin 1 setlinecap\n"); p=2.;q=1;
conto(o,g,w,v,X,Y,M,N, Re(Zo),-p,p);fprintf(o,".03 W 0 1 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, Im(Zo),-p,p);fprintf(o,".03 W 0 1 0 RGB S\n");
for(m=-8;m<8;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q,q);fprintf(o,".007 W 0 .6 0 RGB S\n");
for(m=0;m<8;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q,q);fprintf(o,".007 W .9 0 0 RGB S\n");
for(m=0;m<8;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q,q);fprintf(o,".007 W 0 0 .9 RGB S\n");
for(m= 1;m<17;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-q,q);fprintf(o,".02 W .8 0 0 RGB S\n");
for(m= 1;m<17;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-q,q);fprintf(o,".02 W 0 0 .8 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-p,p); fprintf(o,".02 W .5 0 .5 RGB S\n");
for(m=-16;m<17;m++)conto(o,g,w,v,X,Y,M,N,(0.+m),-q,q);fprintf(o,".02 W 0 0 0 RGB S\n");
fprintf(o,"0 setlinejoin 0 setlinecap\n");
M(Re(Zo),Im(Zo))L(-4,Im(Zo)) fprintf(o,"1 1 1 RGB .022 W S\n");
DO(n,40){M(Re(Zo)-.2*n,Im(Zo))L(Re(Zo)-.2*(n+.4),Im(Zo)) }
fprintf(o,"0 0 0 RGB .032 W S\n");
fprintf(o,"showpage\n");
fprintf(o,"%c%cTrailer\n",'%','%');
fclose(o); free(f); free(g); free(w);
system("epstopdf exp1map.eps");
system( "open exp1map.pdf"); //for macintosh
getchar(); system("killall Preview"); // For macintosh
}
Latex generator of labels
%
\documentclass[12pt]{article}
\usepackage{geometry}
\paperwidth 824pt
\paperheight 426pt
\usepackage{graphics}
\usepackage{rotating}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\textwidth 810pt
\topmargin -105pt
\oddsidemargin -74pt
\pagestyle{empty}
\parindent 0pt
\newcommand \sx {\scalebox}
\begin{document}
\begin{picture}(820,420)
\put(20,20){\includegraphics{exp1map}}
\put(4,412){\sx{2.2}{$y$}}
\put(4,313){\sx{2.2}{$3$}}
\put(4,213){\sx{2.2}{$2$}}
\put(4,113){\sx{2.2}{$1$}}
\put(4,16){\sx{2.2}{$0$}}
\put(2,0){\sx{2.2}{$-4$}}
\put(100,0){\sx{2.2}{$-3$}}
\put(200,0){\sx{2.2}{$-2$}}
\put(300,0){\sx{2.2}{$-1$}}
\put(420,0){\sx{2.2}{$0$}}
\put(520,0){\sx{2.2}{$1$}}
\put(620,0){\sx{2.2}{$2$}}
\put(720,0){\sx{2.2}{$3$}}
\put(811,0){\sx{2.2}{$x$}}
\put(140,329){\sx{2.4}{$v\!=\!0$}}
\put(260,290){\sx{2}{\rot{-45} $u\!=\!-0.2$ \ero}}
\put(324,318){\sx{2}{\rot{-60} $u\!=\!-0.4$ \ero}}
\put(362,330){\sx{2}{\rot{-64} $u\!=\!-0.6$ \ero}}
\put(262,190){\sx{2}{\rot{ 64} $v\!=\!0.2$ \ero}}
\put(332,182){\sx{2}{\rot{ 66} $v\!=\!0.4$ \ero}}
\put(373,180){\sx{2}{\rot{ 70} $v\!=\!0.6$ \ero}}
\put(400,180){\sx{2}{\rot{ 70} $v\!=\!0.8$ \ero}}
\put(424,180){\sx{2.2}{\rot{ 70} $v\!=\!1$ \ero}}
\put(454,178){\sx{1.9}{\rot{ 70} $v\!=\!\Im(L)$ \ero}}
\put(495,178){\sx{2}{\rot{ 75} $v\!=\!2$ \ero}}
\put(535,178){\sx{2}{\rot{ 75} $v\!=\!3$ \ero}}
%\put(40,180){\sx{2}{$u=0$}}
\put(140,171){\sx{2.4}{$u\!=\!0$}}
%
\put(262,22){\sx{2}{\rot{ 70} $u\!=\!0.2$ \ero}}
\put(306,22){\sx{2}{\rot{ 69} $u\!=\!\Re(L)$ \ero}}
\put(332,22){\sx{2}{\rot{ 70} $u\!=\!0.4$ \ero}}
\put(372,22){\sx{2}{\rot{ 70} $u\!=\!0.6$ \ero}}
\put(402,22){\sx{2}{\rot{ 70} $u\!=\!0.8$ \ero}}
\put(425,22){\sx{2.2}{\rot{ 70} $u\!=\!1$ \ero}}
\put(496,22){\sx{2.2}{\rot{ 73} $u\!=\!2$ \ero}}
\put(536,22){\sx{2.2}{\rot{ 73} $u\!=\!3$ \ero}}
\end{picture}
\end{document}
%
References
http://www.ams.org/journals/bull/1993-29-02/S0273-0979-1993-00432-4/S0273-0979-1993-00432-4.pdf Walter Bergweiler. Iteration of meromorphic functions. Bull. Amer. Math. Soc. 29 (1993), 151-188.
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf D. Kouznetsov. Solution of F(x+1)=exp(F(x)) in complex z-plane. 78, (2009), 1647-1670
http://www.ils.uec.ac.jp.jp/~dima/PAPERS/2009vladie.pdf (English) http://mizugadro.mydns.jp/PAPERS/2010vladie.pdf (English) http://mizugadro.mydns.jp/PAPERS/2009vladir.pdf (Russian version) D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
http://reference.wolfram.com/mathematica/ref/Nest.html Nest, Wolfram Mathematica 9 Documentation center, 2013
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 11:40, 28 July 2013 |  | 2,281 × 1,179 (1.14 MB) | T (talk | contribs) | shift for 2 px to left |
| 20:42, 26 July 2013 |  | 1,711 × 885 (722 KB) | T (talk | contribs) | Complex map of the first iteration of exponent in the upper half-plane, $u+\mathrm i v = \mathrm{tet}(1.+\mathrm{ate}(z))=\exp(z)$ in the $z=x+\mathrm i y$ plane. Category:Arctetration Category:Complex map Category:Exponent [[Cate... |
You cannot overwrite this file.
File usage
The following page uses this file: