Ctudent
Identifier Ctudent is used in TORI (and perhaps only in TORI) to denote the «Cumulative function for the Student t-distribution».
In is just integral of density of the Student Distribution:
\( \displaystyle \mathrm{Ctudent}_n(x) = \int_0^x \mathrm{Student}_n(y) \ \mathrm d y \)
In most of the practical applications, both the \(\mathrm{Student}_n(x)\) and \(\mathrm{Ctudent}_n(x)\) appear with real \(x\) and positive integer \(n\); and not so big; for large \(n\), the Gauss distribution is used instead.
Explicit plots
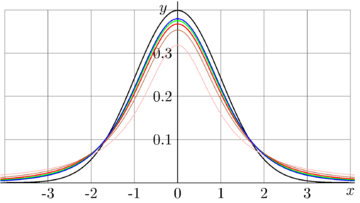
\( y = \mathrm{Student}_n(x)\)
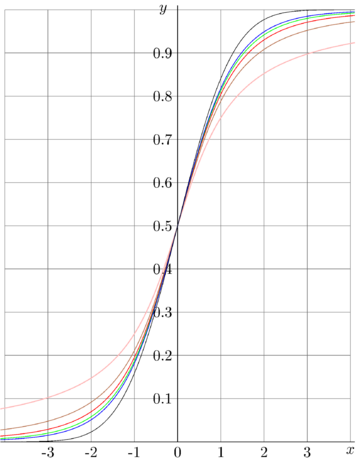
\( y = \mathrm{Ctudent}_n(x)\)
versus \(x\) are shown in figures at right for
\( n = 1 \) (pink), the same as for the Cauchi Distribution
\( n = 2 \) (brown)
\( n = 3 \) (red)
\( n = 4 \) (green)
\( n = 5 \) (blue)
\( n = \infty \) (black), the same as for the Normal Distribution
Function Ctudent is useful in interpretation of experimental data with poor statistics, whine only few measurements are available, and one try to estimate, what is probability to cover the «true value» with some interval calculated from the spreading of the data.
Explicit representation
Wikipedia suggests explicit expressions for the first five Students and Students.
These exressions are used to plot the pictures at right.
The table is copy pasted below with minimal TORIfication:
| \(\ \nu\ \) | PDF: \(\mathrm{Student}(\nu,t)\) | CDF: \(\mathrm{Ctudent}(\nu,t)\) | See also |
|---|---|---|---|
| 1 | \(\ \frac{\ 1\ }{\ \pi\ (1 + t^2)\ }\ \) | \(\ \frac{\ 1\ }{ 2 } + \frac{\ 1\ }{ \pi }\ \arctan(\ t\ )\ \) | Cauchy distribution |
| 2 | \(\ \frac{ 1 }{\ 2\ \sqrt{2\ }\ \left(1+\frac{t^2}{2}\right)^{3/2}}\ \) | \(\ \frac{ 1 }{\ 2\ }+\frac{ t }{\ 2\sqrt{2\ }\ \sqrt{ 1 + \frac{~ t^2\ }{ 2 }\ }\ }\ \) | |
| 3 | \(\ \frac{ 2 }{\ \pi\ \sqrt{3\ }\ \left(\ 1 + \frac{~ t^2\ }{ 3 }\ \right)^2\ }\ \) | \(\ \frac{\ 1\ }{ 2 } + \frac{\ 1\ }{ \pi }\ \left[ \frac{ \left(\ \frac{ t }{\ \sqrt{3\ }\ }\ \right) }{ \left(\ 1 + \frac{~ t^2\ }{ 3 }\ \right) } + \arctan\left(\ \frac{ t }{\ \sqrt{3\ }\ }\ \right)\ \right]\ \) | |
| 4 | \(\ \frac{\ 3\ }{\ 8\ \left(\ 1 + \frac{~ t^2\ }{ 4 }\ \right)^{5/2}}\ \) | \(\ \frac{\ 1\ }{ 2 } + \frac{\ 3\ }{ 8 } \left[\ \frac{ t }{\ \sqrt{ 1 + \frac{~ t^2\ }{ 4 } ~}\ } \right] \left[\ 1 - \frac{~ t^2\ }{\ 12\ \left(\ 1 + \frac{~ t^2\ }{ 4 }\ \right)\ }\ \right]\ \) | |
| 5 | \(\ \frac{ 8 }{\ 3 \pi \sqrt{5\ }\left(1+\frac{\ t^2\ }{ 5 }\right)^3\ }\ \) | \(\ \frac{\ 1\ }{ 2 } + \frac{\ 1\ }{\pi}{ \left[ \frac{ t }{\ \sqrt{5\ }\left(1 + \frac{\ t^2\ }{ 5 }\right)\ } \left(1 + \frac{ 2 }{\ 3 \left(1 + \frac{\ t^2\ }{ 5 }\right)\ }\right) + \arctan\left( \frac{ t }{\ \sqrt{\ 5\ }\ } \right)\right]}\ \) | |
| \(\ \infty\ \) | \(\ \frac{ 1 }{\ \sqrt{2 \pi\ }\ }\ e^{-t^2/2}\) | \(\ \frac{\ 1\ }{ 2 }\ {\left[ 1 + \operatorname{erf}\left( \frac{ t }{\ \sqrt{2\ }\ } \right) \right]}\ \) | Normal distribution, Error function |
These representations are used to generate the explicit plots pf these functions
C++ implementation
// The C++ float routine below follows from the second column of the table above.
float Ctudent1(float x){ return .5 + M_1_PI * atan(x); }
float Ctudent2(float x){ return .5 + x/sqrt(8+4*x*x); }
float Ctudent3(float x){ float y=x/sqrt(3.); return .5 + M_1_PI*( y/(1+y*y) + atan(y) ); }
float Ctudent4(float x){ float y=x/sqrt(4.+x*x); return .5 + .75*y*(1.-y*y/3.); }
float Ctudent5(float x){ return .5 + M_1_PI * ( x/sqrt(5.)/(1.+x*x/5.)*(1.+(2./3.)/(1+x*x/5.)) + atan(x/sqrt(5.)) ); }
Apology
The new notation «Ctudent» and
the numerical implementations are loaded at TORI to simplify the search and the application of the algorithms.
References
Keywords
«Cauchi Distribution», «Ctudent», «Gauss», «Student», «[[]]», «[[]]»,