Difference between revisions of "Hellmuth Kneser"
(Created page with "<div style="float:right; width:180px"> 200px Hellmuth Kneser, 1930 <ref> https://opc.mfo.de/detail?photoID=2180 Kneser, Hellmuth Annotation: c...") |
(→Tetration) |
||
| (16 intermediate revisions by the same user not shown) | |||
| Line 44: | Line 44: | ||
==[[Kneser-Suss inequality]]== |
==[[Kneser-Suss inequality]]== |
||
| − | In 1932, Kneser and [[Wilhelm Suss]] suggest the |
+ | In 1932, Kneser and [[Wilhelm Suss]] suggest the [[Kneser-Suss unequality]] |
<ref>https://www.jstor.org/stable/24529990?seq=1 |
<ref>https://www.jstor.org/stable/24529990?seq=1 |
||
H. Kneser and W. Suss, Die Volumina in linearen Scharen konvexer korper, Matematisk Tidsskrift. B (1932), 19-25. |
H. Kneser and W. Suss, Die Volumina in linearen Scharen konvexer korper, Matematisk Tidsskrift. B (1932), 19-25. |
||
| Line 75: | Line 75: | ||
==[[Tetration]]== |
==[[Tetration]]== |
||
| + | <div class="thumb tright" style="float:right;width:230px"> |
||
| + | [[File:Tetreal10bx10d.png|250px]] |
||
| + | \(y={\rm tet}_b(x)~~\) versus \(x\) for various \(b\) |
||
| + | [[File:Qexpmap.jpg|250px]] |
||
| − | In 1950, Kneser publishes paper |
||
| + | [[Complex map]] |
||
| + | \( p\!+\!\mathrm{i} q=\varphi(x\!+\!\mathrm{i} y) \) |
||
<ref> |
<ref> |
||
| + | http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf D.Kouznetsov, H.Trappmann. Superfunctions and sqrt of Factorial. (2010) |
||
| + | </ref> |
||
| + | </div> |
||
| + | |||
| + | In 1950, Kneser publishes paper |
||
| + | <ref name="k"> |
||
http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi |
http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi |
||
[[Hellmuth Kneser]]. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen. |
[[Hellmuth Kneser]]. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen. |
||
| Line 87: | Line 98: | ||
There, the need to construct [[superfunction]] of exponential, id est, [[tetration]], is formulated. |
There, the need to construct [[superfunction]] of exponential, id est, [[tetration]], is formulated. |
||
| − | [[Tetration]] to base \( b\) appears as holomorphic solution |
+ | [[Tetration]] to base \( b\) appears as holomorphic solution \( F= \mathrm{tet}_b \) |
| + | of the [[Transfer equation]] \( F(z+1) = b^{F(z)} \) |
||
| − | \( F= \mathrm{tet}_b \) |
||
| + | with additional condition \( F(0)=1 \) |
||
| − | of the [[Transfer equation]] |
||
| + | and certain behaviors at infinity (approaching the [[fixed point]](s) of \( \exp_b \) |
||
| − | \( F(z+1) = b^{F(z)} \) |
||
| + | at \( \pm \mathrm i\infty \) ). These conditions are necessary for the uniqueness of the solution. |
||
| + | Then, during a half-century, various approaches to evaluation of [[tetration]] had been reported. |
||
| − | \( F(0)=1 \) |
||
| − | |||
| − | with certain behaviors at infinity (approaching the [[fixed point]](s) of \( \exp_b \) |
||
| − | at \( \pm \mathrm i\infty \) ). |
||
| − | |||
| − | Then, during a century, various approaches to evaluation of [[tetration]] had been reported. |
||
Since 2009, the efficient algorithms for evaluation of [[tetration]] to various values of base (and the corresponding [[complex map]]s) are available. |
Since 2009, the efficient algorithms for evaluation of [[tetration]] to various values of base (and the corresponding [[complex map]]s) are available. |
||
| Line 126: | Line 133: | ||
</ref><ref> |
</ref><ref> |
||
https://link.springer.com/article/10.1007/s10444-018-9615-7 William Paulsen. Tetration for complex bases. Advances in Computational Mathematics, 2018.06.02. |
https://link.springer.com/article/10.1007/s10444-018-9615-7 William Paulsen. Tetration for complex bases. Advances in Computational Mathematics, 2018.06.02. |
||
| + | </ref> |
||
| + | |||
| + | With [[tetration]] \( F=\mathrm{tet} \) |
||
| + | |||
| + | and the inverse function \( G=F^{-1} \), id est, [[arctetration]] \( G=\mathrm{ate} \) , |
||
| + | |||
| + | the function \( \varphi \), mentioned in the original title by Kneser, can be expressed as follows: |
||
| + | |||
| + | \( \varphi(x)= F(1/2+G(x)) \) |
||
| + | |||
| + | [[Complex map]] of function \( \varphi \) (metioned in the title of paper <ref name="k"/> is shown in figure at right.<br> |
||
| + | This map is right hand side of figure 4 (or figure 5) of publication |
||
| + | <ref> |
||
| + | http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf <br> |
||
| + | http://mizugadro.mydns.jp/PAPERS/2010superfae.pdf <br> |
||
| + | http://mizugadro.mydns.jp/PAPERS/2010superfar.pdf <br> |
||
| + | D.Kouznetsov, H.Trappmann. Superfunctions and sqrt of Factorial. |
||
| + | SSN 00271349, Moscow University Physics Bulletin, 2010, Vol. 65, No. 1, pp. 6–12. © Allerton Press, Inc., 2010. Published in Russian in Vestnik Moskovskogo Universiteta. Fizika, 2010, No. 1, pp. 8–14. |
||
| + | Abstract — The holomorphic function h is constructed such that h(h(z))=z! ; this function is interpreted as square root of Factorial. |
||
</ref> |
</ref> |
||
| Line 172: | Line 198: | ||
[[Kneser-Suss inequality]], |
[[Kneser-Suss inequality]], |
||
| + | [[Square root of exponential]], |
||
[[Superfunction]], |
[[Superfunction]], |
||
[[Tetration]] |
[[Tetration]] |
||
Revision as of 22:18, 30 November 2019
 Hellmuth Kneser, 1930
[1]
Hellmuth Kneser, 1930
[1]
 Hellmuth Kneser, 1958
[2]
Hellmuth Kneser, 1958
[2]
Hellmuth Kneser (1898.04.16, Tartu (Dortpart), Estonia - 1973.08.23, Tubingen) is Estonian and German mathematician. [3]
Biography
Since 1916, education at Wroclaw University
Since 1921, work with Dufit Hilbert on foundation of quantum mechanics ("Untersuchungen zur Quantentheorie")
Since 1944, work at the Mathematical Research Institute of Oberwolfach
at 1954, president of the German Mathematical Society.
Kneser-Suss inequality
In 1932, Kneser and Wilhelm Suss suggest the Kneser-Suss unequality [4][5][6]:
In the convex geometry setting, let \( K, L ∈ \mathfrak{K}^n\) be convex bodies, and let \(M\) be the convex body satisfying
\( S(M^{n−1};·) = S(K^{n−1};·) + S(L^{n−1};·) \)
Then
\( \mathrm{vol}(M)^{n-1/n} \ge \mathrm{vol}(K)^{n-1/n} + \mathrm{vol}(L)^{n-1/n} \)
Tetration
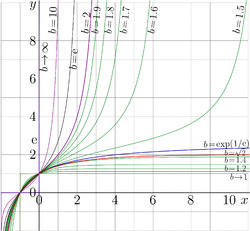 \(y={\rm tet}_b(x)~~\) versus \(x\) for various \(b\)
\(y={\rm tet}_b(x)~~\) versus \(x\) for various \(b\)
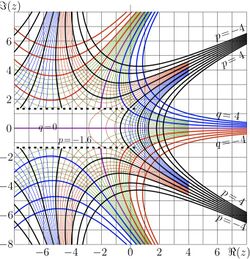 Complex map
\( p\!+\!\mathrm{i} q=\varphi(x\!+\!\mathrm{i} y) \)
[7]
Complex map
\( p\!+\!\mathrm{i} q=\varphi(x\!+\!\mathrm{i} y) \)
[7]
In 1950, Kneser publishes paper [8] entitled
Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen.
There, the need to construct superfunction of exponential, id est, tetration, is formulated.
Tetration to base \( b\) appears as holomorphic solution \( F= \mathrm{tet}_b \)
of the Transfer equation \( F(z+1) = b^{F(z)} \)
with additional condition \( F(0)=1 \)
and certain behaviors at infinity (approaching the fixed point(s) of \( \exp_b \) at \( \pm \mathrm i\infty \) ). These conditions are necessary for the uniqueness of the solution.
Then, during a half-century, various approaches to evaluation of tetration had been reported.
Since 2009, the efficient algorithms for evaluation of tetration to various values of base (and the corresponding complex maps) are available. [9][10][11][12][13][14][15][16]
With tetration \( F=\mathrm{tet} \)
and the inverse function \( G=F^{-1} \), id est, arctetration \( G=\mathrm{ate} \) ,
the function \( \varphi \), mentioned in the original title by Kneser, can be expressed as follows:
\( \varphi(x)= F(1/2+G(x)) \)
Complex map of function \( \varphi \) (metioned in the title of paper [8] is shown in figure at right.
This map is right hand side of figure 4 (or figure 5) of publication
[17]
Relatives
Adolf Kneser (1862.03.19, Grüssow, Mecklenburg, Germany - 1930.01.24, Breslau, Germany (Wrocław, Poland)), father
Laura Kneser (aka Laura Booth) (1869.07.18 - 1944.07.18), mother [18]
Lorenz Friedrich Kneser (1896.oo.oo - 1918.oo.oo), brother
Hans Otto Kneser (1901.oo.oo - 1985.oo.oo), brother
Dorothee Beer (aka Dorothee Kneser) (1905.oo.oo - 1968.oo.oo), sister
Hertha Kneser (aka Hertha Scheuerlen) (1900.oo.oo - 1980.oo.oo), wife
Martin Kneser (1928.01.21 - 2004.02.16), son
References
- ↑ https://opc.mfo.de/detail?photoID=2180 Kneser, Hellmuth Annotation: ca. 1930 Author: Jacobs, Konrad (photos provided by Jacobs, Konrad)
- ↑ https://opc.mfo.de/detail?photo_id=7607 On the Photo: Kneser, Hellmuth Location: Oberwolfach Author: Danzer, Ludwig (photos provided by Danzer, Ludwig) Source: L. Danzer, Dortmund Year: 1958 Copyright: L. Danzer, Dortmund Photo ID: 7607
- ↑ https://www.geni.com/people/Hellmuth-Kneser/6000000000328937967 Hellmuth Kneser Birthdate: April 16, 1898 Birthplace: Tartu, Tartumaa, Estonia Death: August 23, 1973 (75) Tübingen, Tübingen, Baden-Württemberg, Germany Immediate Family: Son of Adolf Kneser and Laura Kneser Husband of Hertha Kneser Brother of Lorenz Friedrich Kneser; Hans Otto Kneser and Dorothee Beer Managed by: Martin Severin Eriksen Last Updated: May 24, 2018
- ↑ https://www.jstor.org/stable/24529990?seq=1 H. Kneser and W. Suss, Die Volumina in linearen Scharen konvexer korper, Matematisk Tidsskrift. B (1932), 19-25.
- ↑ https://hal.archives-ouvertes.fr/hal-00564691/document Dorin BUCUR, Ilaria FRAGALA`, Jimmy LAMBOLEY. Optimal convex shapes for concave functionals. February 9, 2011. Motivated by a long-standing conjecture of Po ́lya and Szego ̈ about the Newtonian capacity of convex bodies, we discuss the role of concavity inequalities in shape optimization, and we provide several counterexamples to the Blaschke-concavity of variational functionals, including capacity. We then introduce a new algebraic structure on convex bodies, which allows to obtain global concavity and indecomposability results, and we discuss their application to isoperimetric- like inequalities. As a byproduct of this approach we also obtain a quantitative version of the Kneser-Su ̈ss inequality. Finally, for a large class of functionals involving Dirichlet energies and the surface measure, we perform a local analysis of strictly convex portions of the boundary via second order shape derivatives. This allows in particular to exclude the presence of smooth regions with positive Gauss curvature in an optimal shape for Po ́lya-Szego ̈ problem.
- ↑ https://www2.bc.edu/brian-lehmann/papers/AlgCvxg.pdf BRIAN LEHMANN AND JIAN XIAO. CORRESPONDENCES BETWEEN CONVEX GEOMETRY AND COMPLEX GEOMETRY. (2019) Abstract. We present several analogies between convex geometry and the theory of holomorphic line bundles on smooth projective varieties or Ka ̈hler manifolds. We study the relation between positive products and mixed volumes. We define and study a Blaschke addition for divisor classes and mixed divisor classes, and prove new geometric inequalities for divisor classes. We also reinterpret several classical convex geometry results in the context of algebraic geometry: the Alexandrov body construc- tion is the convex geometry version of divisorial Zariski decomposition; Minkowski’s existence theorem is the convex geometry version of the duality between the pseudo-effective cone of divisors and the movable cone of curves. // .. 7.1. Kneser-Suss inequality for divisors. ..
- ↑ http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf D.Kouznetsov, H.Trappmann. Superfunctions and sqrt of Factorial. (2010)
- ↑ 8.0 8.1 http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi Hellmuth Kneser. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen. Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67
- ↑
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
D.Kouznetsov. (2009). Solutions of F(z+1)=exp(F(z)) in the complex plane. Mathematics of Computation, 78: 1647-1670. DOI:10.1090/S0025-5718-09-02188-7 - ↑ http://www.ils.uec.ac.jp/~dima/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45
- ↑
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf
http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756. - ↑ http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf http://www.ils.uec.ac.jp/~dima/PAPERS/2011e1e.pdf H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). Mathematics of computation, 2012 February 8.
- ↑ http://journal.kkms.org/index.php/kjm/article/view/428 William Paulsen. Finding the natural solution to f(f(x))=exp(x). Korean J. Math. Vol 24, No 1 (2016) pp.81-106.
- ↑ https://link.springer.com/article/10.1007/s10444-017-9524-1 William Paulsen, Samuel Cowgill. Solving F(z + 1) = b F(z) in the complex plane. Advances in Computational Mathematics, December 2017, Volume 43, Issue 6, pp 1261–1282
- ↑ https://search.proquest.com/openview/cb7af40083915e275005ffca4bfd4685/1?pq-origsite=gscholar&cbl=18750&diss=y Cowgill, Samuel. Exploring Tetration in the Complex Plane. Arkansas State University, ProQuest Dissertations Publishing, 2017. 10263680.
- ↑ https://link.springer.com/article/10.1007/s10444-018-9615-7 William Paulsen. Tetration for complex bases. Advances in Computational Mathematics, 2018.06.02.
- ↑
http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf
http://mizugadro.mydns.jp/PAPERS/2010superfae.pdf
http://mizugadro.mydns.jp/PAPERS/2010superfar.pdf
D.Kouznetsov, H.Trappmann. Superfunctions and sqrt of Factorial. SSN 00271349, Moscow University Physics Bulletin, 2010, Vol. 65, No. 1, pp. 6–12. © Allerton Press, Inc., 2010. Published in Russian in Vestnik Moskovskogo Universiteta. Fizika, 2010, No. 1, pp. 8–14. Abstract — The holomorphic function h is constructed such that h(h(z))=z! ; this function is interpreted as square root of Factorial. - ↑ https://www.geni.com/people/Laura-Kneser/6000000025507101855 Laura Kneser (Booth) Birthdate: July 18, 1869 Death: 1944 (74-75) Immediate Family: Daughter of Joachim Lorenz de la Camp Booth and Laura Caroline Booth Wife of Adolf Kneser Mother of Lorenz Friedrich Kneser; Hellmuth Kneser; Hans Otto Kneser and Dorothee Beer Sister of Harriet Küstner; Martha Booth; Elisabeth Booth and Alice Booth Managed by: Private User Last Updated: February 15, 2016
https://en.wikipedia.org/wiki/Hellmuth_Kneser
http://litten.de/fulltext/cara.htm Freddy Litten. Die Carathéodory-Nachfolge in München 1938-1944 [ursprünglich erschienen in Centaurus. International Magazine of the History of Mathematics, Science, and Technology, Band 37, Heft 2, 1994, S. 154-172. Bei Übernahme von Informationen bzw. Interpretationen aus diesem Beitrag bitte vorzugsweise die gedruckte Version zitieren, oder diese unter Angabe von Autor, Titel und vollständigem URL.]. .. Obwohl von Faber einen neuen Berufungsvorschlag in Aussicht gestellt hatte, kam es vorerst nicht dazu. Der Grund war wiederum, wie das Kultusministerium dem Reichsministerium auf Anfrage vom 22. Januar 1941 mitteilte, daß sich Fakultät und Dozentenschaft nicht einigen konnten [BayHStA, 12.2.1941]. Am 24. Januar benannten die Münchener Mathematiker einige Personen, "die zwar den früher Genannten an wissenschaftlicher Bedeutung nicht gleichkommen, jedoch für ein Ordinariat an der Universität München in Betracht kommen können." Dabei handelte es sich um Heinrich Behnke (geboren 1898, 1927 o. Professor in Münster/Westfalen), der "einer der besten Kenner der Theorie der analytischen Funktionen von mehreren Veränderlichen" sei und zudem "einer der erfolgreichsten Lehrer, die wir in Deutschland haben ..."; Hellmuth Kneser (1898 geboren, 1925 o. Professor in Greifswald, 1937 in Tübingen), "ein vielseitiger, tief veranlagter Forscher", dessen Arbeiten zur Theorie der Funktionen mehrerer komplexer Veränderlicher besonders zu erwähnen seien; Franz Rellich (1906 geboren, 1942 o. Professor in Dresden), ein "ideen- und erfolgreicher Forscher, von dem gewiß noch manche wertvolle Bereicherung der Wissenschaft zu erwarten ist"; und schließlich Herbert Seifert (geboren 1907, 1935 Vertretung einer Professur in Heidelberg, 1937 o. Professor Heidelberg), dessen topologische Arbeiten ihn für den Münchener Lehrstuhl in Frage kommen ließen [UAM, NC].
Keywords
Kneser-Suss inequality, Square root of exponential, Superfunction, Tetration