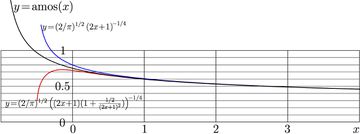
Amplitude of oscillator function
Amplitude of oscillator function \(A_n\!=\)Amos\((n)\), for even \(n\), is amplitude of value of the oscillator function at zero,
\(A(n)= \psi_n(0)\)
where \(\psi_n(z)=\frac{1}{\sqrt{N_n}}\)HermiteH\(_n(z)\, \exp(-z^2/2)\) is oscillator function, normalised solution of the stationary Schroedinger equation for the Harmonic oscillator. here, HermiteH\(_n\) denotes the \(n\)th Hermite polynomial and \(N_n\) is its norm.
For the asymptotic expansions of various functions with the oscillator function, the asymptotic behaviour of \(A(n)\) at large values of \(n\) is important.
For given number \(n\) of the oscillator function, In fomulas, this function can be denoted with \(A_n\), or with \(A(n)\), or, if letter \(A\) is already occupied for other object, the more long name amos. In general, function Amos=amos can be treated as function of complex argument. For real values of the argument, this function and its asymptotic approximation are shown in figure at right, together with two its asymptotic approximations.
Hermite number
Value of the oscillator function at zero is determined by the Hermite number. It can be considered as function of number \(n\) of the oscillator function.
There is special name for
\(H_n=H_n(0)=\mathrm{HermiteH}[n,0]\).
It is called Hermite number; originally, \(H_n\) is defined only for integer \(n\). [1]
\(\displaystyle H_n= \frac {2^n \sqrt{\pi}} {\displaystyle \mathrm{Factorial}\left(- \frac{1\!+\!n}{2}\right)}\) \(\displaystyle = \left\{ \begin{array}{ccc} 0 & \mathrm{for ~ odd} & n \\ \displaystyle (-1)^{n/2} \frac{n!}{(n/2)!} &\mathrm{for ~ even} & n \end{array} \right.\)
Then, the amplitude of oscillation of the oscillator function in vicinity of zero, at least for even \(n\), can be expressed through the Hermite number as follows
\(\displaystyle A_n=|F_n(0)|= \frac{|H_n|}{\sqrt{N_n}} \) \(= \displaystyle \frac{\frac{n!}{(n/2)!}}{\sqrt{2^n n! \sqrt{\pi}}} \) \(= \displaystyle \frac{\sqrt{n! / \sqrt{\pi}}} {2^{n/2} (n/2)! } \)
Generalisation
In order to test various representations of the Amplitude of oscillator function \(A_n\), as well as the modifications for similar cases, it worth to treat it as holomorphic suction of complex argument \(n\).
In particular, this provides the amplitude of oscillations of the oscillator function \(F_n(x)\) at large \(n\) and moderate \(x\) for even \(n\). This may be especially important for large \(n\), id huge amount of modes is necessary to take into account in order to describe, for example, the efficiency of channelling of a quantum particle by absorbing walls.
The range of holorpism or the original representation of \(A_n\) through \(\sqrt{n!}\) is limited by the cut line of function \(\sqrt{\,}\).
For this reason, it worth to redefine Amplitude of oscillator function as follows:
\(\displaystyle A_n=A(n)=\mathrm{amos}(n)=\pi^{-1/4} \) \(\displaystyle \exp\left(\frac{1}{2}\mathrm{lof}(n)-\mathrm{lof}(n/2)-\ln(2)\, n/2\big)\right)\)
where lof is holomorphic extension of logarithm of factorial; in vicinity of the positive part of the real axis,
\(\mathrm{lof}(z)= \ln(\mathrm{Factorial}(z)) = \ln(z!)\)
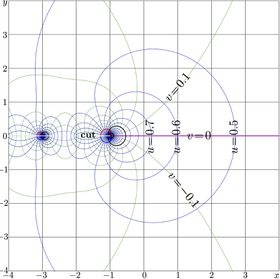
Function amos can be interpreted complex function of complex argument. The map of this function is shown in figure at right with lines \(u\!=\)const\(~\) and lines \(v\!=\)const\(~\) for \(u\!+\!\mathrm i v=\,\)amos\((x\!+\!\mathrm i y)\)
Asymptotics at large values of the argument
For large values of argument, amplitude of oscillator function can be represented with asymptotic series
\(A_n\approx \frac{(2/n)^{1/4}}{\sqrt{\pi}} \) \( \left( 1-\frac{1}{8n}+\frac{1}{128 n^2}+\frac{21}{1024 n^3}-\frac{85}{32768 n^4} -\frac{6511}{262144 n^5}+\frac{13989}{4194304n^6}+\frac{2539085}{33554432 n^7} -\frac{21469709}{2147483648 n^8} -\frac{7385563163 }{17179869184 n^9} +\frac{15306326687 }{274877906944 n^{10}} %+\frac{8625737936387 }{2199023255552 n^{11}} %-\frac{35288423873601 }{70368744177664 n^{12}} %-\frac{29542243391383163 }{562949953421312 n^{13}} %+\frac{59967901184881517 }{9007199254740992 n^{14}} %+\frac{69743016827113388925 }{72057594037927936 n^{15}} %-\frac{1127507014234512448061 }{9223372036854775808 n^{16}} %-\frac{1736837605178928412140179 }{73786976294838206464 n^{17}} %+\frac{3500257705125381294286523 }{1180591620717411303424 n^{18}} %+\frac{6893220525032150345744187527 }{9444732965739290427392 n^{19}} %-\frac{27734856867682323334288371163 }{302231454903657293676544 n^{20}} +O\left(\frac{1}{n^{11}}\right) \right) \)
For large values of number of mode, say \)n>20$, such a representation provides of order of 16 decimal digits, that corresponds to the best precision available with complex double arithmetics.
References
- ↑ http://mathworld.wolfram.com/HermiteNumber.html Weisstein, Eric W. "Hermite Number." From MathWorld--A Wolfram Web Resource.
Keywords
Hermite number, Germite Gaussian mode, Oscillator function, Quantum mechanics