Entire Function with Logarithmic Asymptotic

Term Entire Function with Logarithmic Asymptotic appears as title of publication at Applied Mathematical Sciences, 2013.

Term Entire Function with Logarithmic Asymptotic can make an impression of an oxymoron:
function logarithm has cut line, that cannot be reproduced with an entire function.

Term Entire Function with Logarithmic Asymptotic refers to the sectorial asymptotic:
in some sector with vertex at the origin, the function grows in a way, similar to that of Logarithm.
This sector cannot include the negative part of the real axis: there, the Logarithm is not a continuous function.
However the sector may cover almost all the complex plane, excluding an arbitrary narrow sector along the negative part of the real axis.

Definition

Entire Function with Logarithmic Asymptotic is function \(\Phi\) of complex argument such that

(1) \(\Phi\) is holomorphic in the whole complex plane

(2) in some sector of the complex plane \(\Phi\) approach function Logarithm, id est, there exist real values \(t_1\) and \(t_2\) such that \(-\pi<t_1<t_2<\pi\) and for any fixed real \(t\) with \(t_1<t<t_2\) , \[ \lim_{r \to +\infty} \Big( \Phi(r\exp(\mathrm i t)) - \log(r\exp(\mathrm i t)) \Big) = 0 \]

Superfunctions

The example of an Entire Function with Logarithmic Asymptotic is described also in book "Superfunctions" .

The Entire Function with Logarithmic Asymptotic is expressed through the Superfunction SuTra of the elementary Trappmann function \(\mathrm{tra} = z \mapsto z+\exp(z) \):

\[ \Phi(z) = - \mathrm{SuTra} (-z) \] The complex map of Logarithm and that of function \(\Phi\) above are shown in the pictures below.

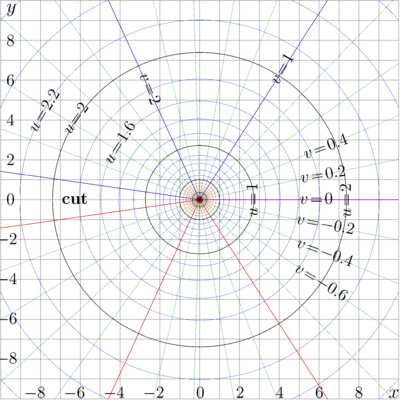
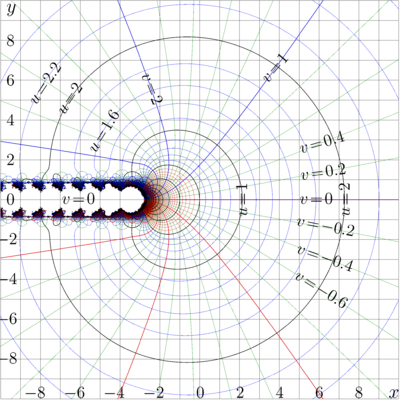
The maps above show function \(f(x\!+\!\mathrm i y) = u + \mathrm i v\ \) with
lines \(u=\rm const \) and
lines \(v=\rm const \)
in the \(x,y\) plane for \(f\!=\!\log\) and for \(f\!=\!\Phi \).

The qualitative geometry of these level lines confirms the main claim about the Entire Function with Logarithmic Asymptotic.

Notes by ChatGPT

The example \(\Phi(z)=-\mathrm{SuTra}(-z)\) described in this article does not appear to be isolated.

A natural way to obtain further candidates for an Entire Function with Logarithmic Asymptotic is to replace the Trappmann function \[ \mathrm{tra}(z)=z+\exp(z) \] by a more general transfer function of the form \[ T_{a,b}(z)=z+a\ \exp(bz), \qquad a\neq 0,\ b\neq 0, \] and to construct a corresponding superfunction \(F_{a,b}\) satisfying \[ T_{a,b}(F_{a,b}(z))=F_{a,b}(z+1), \] with an asymptotic normalization \[ F_{a,b}(z)\sim -\tfrac{1}{b}\log(-z)+C \quad\text{as }\Re z\to -\infty. \]

If such a superfunction \(F_{a,b}\) exists and is entire, then the function \[ \Phi_{a,b}(z)=-F_{a,b}(-z) \] formally satisfies a logarithmic asymptotic \[ \Phi_{a,b}(z)\sim \tfrac{1}{b}\log z - C \] in any sector avoiding the negative real axis.

In this way, logarithmic behavior arises not from analytic continuation of the logarithm itself, but as an asymptotic inverse of exponential dynamics under iteration. This mechanism explains how an entire function may mimic the logarithm in wide sectors of the complex plane while remaining single-valued and holomorphic everywhere.

At present, no examples of Entire Function with Logarithmic Asymptotic are known that do not arise, directly or indirectly, from such superfunction constructions. It is also not known whether all entire functions with logarithmic asymptotic must be obtainable in this way. These questions remain open.

Acknowledgement

This article is created following the advice by ChatGPT.

Some stylistic suggestions by ChatGPT are taken into account.

The section above is generated by ChatGPT after the request from Editor.

References

Keywords

«ChatGPT», «Entire Function with Logarithmic Asymptotic», «Logarithm», «LambertW.cin», «Tania.cin», «Sutran.cin», «SuZex.cin», «Superfunction», «Superfunctions», «SuTra», «SuZex», «Trappmann function»,