Difference between revisions of "File:SuTraPlo3T.jpg"
(Importing image file) |
($ -> \( ; description ; refs ; pre ; keywords) |
||
| (2 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | {{oq|SuTraPlo3T.jpg|Original file (1,262 × 1,694 pixels, file size: 182 KB, MIME type: image/jpeg)|380}} |
||
| − | Importing image file |
||
| + | |||
| + | Fig.20.5 from page 276 of book of «[[Superfunctions]]»<ref> |
||
| + | https://mizugadro.mydns.jp/BOOK/468.pdf |
||
| + | D.Kouznetsov. [[Superfunctions]]. [[Lambert Academic Publishing]], 2020. |
||
| + | </ref>, 2020. |
||
| + | |||
| + | The image is used also as Рис.20.5 at page 284 of the Russian version «[[Суперфункции]]» |
||
| + | <ref> |
||
| + | https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 <br> |
||
| + | https://mizugadro.mydns.jp/BOOK/202.pdf |
||
| + | Д.Кузнецов. [[Суперфункции]]. [[Lambert Academic Publishing]], 2014 |
||
| + | </ref>, 2014. |
||
| + | |||
| + | The figure shows the [[explicit plot]] of function [[SuTra]] and its asymptotic |
||
| + | \( x \mapsto -\ln(-x)\). |
||
| + | |||
| + | The additional horizontal gridline shows \(1\!+\!\mathrm e=\mathrm{SuTra}(2)\) |
||
| + | |||
| + | [[SuTra]] is [[superfunction]] of the [[Trappmann function]] \(\mathrm{tra} = z \mapsto z+\mathrm e^z\). |
||
| + | |||
| + | Function [[SuTra]] satisfies the [[Transfer equation]] |
||
| + | |||
| + | \(\mathrm{tra}(\mathrm{SuTra}(z))=\mathrm{SuTra}(z+1) \) |
||
| + | |||
| + | Here, the [[Trappmann function]] \(\mathrm{tra}\) is treated as a [[Transfer function]]. |
||
| + | |||
| + | Until year 2013, function [[SuTra]] had been believed to be difficult to evaluate (if at al) as the |
||
| + | [[Trappmann function]] has no [[fixed point]].<br> |
||
| + | However, after to guess the asymptotic behavior (thin curve in the explicit plot), the evaluation of [[SuTra]] becomes straightforward.<br> |
||
| + | It is described at [[Applied Mathematical Sciences]] <ref> |
||
| + | https://www.m-hikari.com/ams/ams-2013/ams-129-132-2013/kouznetsovAMS129-132-2013.pdf <br> |
||
| + | https://mizugadro.mydns.jp/PAPERS/2013hikari.pdf |
||
| + | D.Kouznetsov. Entire Function with Logarithmic Asymptotic. [[Applied Mathematical Sciences]], Vol. 7, 2013, no. 131, 6527 - 6541 |
||
| + | </ref>, 2013. |
||
| + | |||
| + | To year 2026, function \(z \mapsto -\mathrm{ZuZex}(-z)\) <br> |
||
| + | seems to be the only reported [[entire function with logarithmic asymptotic]]. |
||
| + | |||
| + | ==[[C++]] generator of curves== |
||
| + | /* Files [[ado.cin]], [[SuZex.cin]], [[LambertW.cin]] and [[Tania.cin]] sould be loaded to the working directory in order to compile the [[C++]] code below */ |
||
| + | <pre> |
||
| + | #include <math.h> |
||
| + | #include <stdio.h> |
||
| + | #include <stdlib.h> |
||
| + | #define DB double |
||
| + | #define DO(x,y) for(x=0;x<y;x++) |
||
| + | using namespace std; |
||
| + | #include<complex> |
||
| + | typedef complex<double> z_type; |
||
| + | #define Re(x) x.real() |
||
| + | #define Im(x) x.imag() |
||
| + | #define I z_type(0.,1.) |
||
| + | #include "Tania.cin" // need for LambertW |
||
| + | #include "LambertW.cin" // need for AuZex |
||
| + | #include "SuZex.cin" |
||
| + | //#include "AuZex.cin" |
||
| + | |||
| + | z_type tra(z_type z){ return exp(z)+z;} |
||
| + | |||
| + | //z_type F(z_type z){ return log(suzex(z));} |
||
| + | //z_type G(z_type z){ return auzex(exp(z));} |
||
| + | |||
| + | z_type sutra(z_type z){ if( Re(z)<2. || fabs(Im(z))>2. ) return log(suzex(z)); |
||
| + | return tra(sutra(z-1.));} |
||
| + | |||
| + | #include "ado.cin" |
||
| + | #define M(x,y) fprintf(o,"%6.4f %6.4f M\n",0.+x,0.+y); |
||
| + | #define L(x,y) fprintf(o,"%6.4f %6.4f L\n",0.+x,0.+y); |
||
| + | main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d; FILE *o;o=fopen("SuTraPlo3.eps","w"); ado(o,604,812); |
||
| + | fprintf(o,"302 202 translate\n 100 100 scale\n"); |
||
| + | fprintf(o,"1 setlinejoin 2 setlinecap\n"); |
||
| + | for(n=-2;n<7;n++) {M(-3,n)L(3,n)} |
||
| + | for(m=-3;m<4;m++) {M(m,-2)L(m,6)} |
||
| + | // M(M_E,0)L(M_E,1) M(0,M_E)L(1,M_E) |
||
| + | M(0,1.+M_E) L(2,1.+M_E) |
||
| + | fprintf(o,".004 W S\n"); |
||
| + | // DO(m,700){x=.01 +.02*m; y=Re(LambertW(LambertW(x)));if(m==0) M(x,y) else L(x,y) if(x>12.03||y>12.03) break;} fprintf(o,".033 W 1 0 0 RGB S\n"); |
||
| + | // DO(m,700){x=.01 +.02*m; y=Re(LambertW(x));if(m==0) M(x,y) else L(x,y) if(x>12.03||y>12.03) break;} fprintf(o,".04 W 1 .5 0 RGB S\n"); |
||
| + | // M(0,0) L(12.03,12.03) fprintf(o,".04 W 0 1 0 RGB S\n"); |
||
| + | DO(m,700){x=-5.02 +.02*m; y=Re(sutra(x)); if(m==0) M(x,y) else L(x,y) if(x>3.03||y>6.1) break;} fprintf(o,".03 W 0 0 1 RGB S\n"); |
||
| + | DO(m,240){x=-5.02 +.02*m; y=-log(-x); if(m==0) M(x,y) else L(x,y) if(x>3.03||y>6.03) break;} fprintf(o,".01 W .5 0 0 RGB S\n"); |
||
| + | fprintf(o,"showpage\n"); fprintf(o,"%c%cTrailer\n",'%','%'); fclose(o); |
||
| + | system("epstopdf SuTraPlo3.eps"); |
||
| + | system( "open SuTraPlo3.pdf"); //for macintosh |
||
| + | getchar(); system("killall Preview"); // For macintosh |
||
| + | } |
||
| + | </pre> |
||
| + | |||
| + | ==[[Latex]] generator of labels== |
||
| + | |||
| + | % file SuTraPlo3.pdf should be generated with the code above in order to compile the Latex document below. |
||
| + | % Copyleft 2012 by Dmitrii Kouznetsov |
||
| + | <pre> |
||
| + | \documentclass[12pt]{article} |
||
| + | \usepackage{geometry} |
||
| + | \usepackage{graphicx} |
||
| + | \usepackage{rotating} |
||
| + | \paperwidth 608pt |
||
| + | \paperheight 816pt |
||
| + | \topmargin -98pt |
||
| + | \oddsidemargin -71pt |
||
| + | \textwidth 900pt |
||
| + | \textheight 900pt |
||
| + | \pagestyle {empty} |
||
| + | \newcommand \sx {\scalebox} |
||
| + | \newcommand \rot {\begin{rotate}} |
||
| + | \newcommand \ero {\end{rotate}} |
||
| + | \newcommand \ing {\includegraphics} |
||
| + | \parindent 0pt |
||
| + | \pagestyle{empty} |
||
| + | \begin{document} |
||
| + | \begin{picture}(602,805) |
||
| + | \put(310,794){\sx{4}{$y$}} |
||
| + | \put(220,566){\sx{3.8}{$1\!+\!\mathrm e$}} |
||
| + | \put(310,690){\sx{4}{$5$}} |
||
| + | \put(310,590){\sx{4}{$4$}} |
||
| + | \put(310,490){\sx{4}{$3$}} |
||
| + | \put(310,390){\sx{4}{$2$}} |
||
| + | \put(310,289){\sx{4}{$1$}} |
||
| + | \put(312,187){\sx{4}{$0$}} |
||
| + | \put(290, 87){\sx{4}{$-\!1$}} |
||
| + | %\put(325,098){\sx{4}{$0$}} |
||
| + | |||
| + | \put(068,206){\sx{4}{$-\!2$}} |
||
| + | \put(168,206){\sx{4}{$-\!1$}} |
||
| + | \put(291,206){\sx{4}{$0$}} |
||
| + | \put(392,206){\sx{4}{$1$}} |
||
| + | \put(492,206){\sx{4}{$2$}} |
||
| + | \put(578,206){\sx{4}{$x$}} |
||
| + | |||
| + | \put(462,308){\sx{4.2}{\rot{70}$y\!=\!\mathrm{SuTra}(x)$\ero}} |
||
| + | \put(44,314){\sx{3.8}{\rot{0}$y\!=\!-\!\ln(-\!x)$\ero}} |
||
| + | %\put(10,10){\ing{ExpQ2plot}} |
||
| + | %\put(10,10){\ing{SuZexPlot511}} |
||
| + | \put(0,0){\ing{SuTraplo3}} |
||
| + | %\put(0,0){\ing{SuTraplo3}} |
||
| + | \end{picture} |
||
| + | \end{document} |
||
| + | </pre> |
||
| + | ==References== |
||
| + | {{ref}} |
||
| + | |||
| + | {{fer}} |
||
| + | ==Keywords== |
||
| + | «[[ado.cin]]», |
||
| + | «[[SuZex.cin]]», |
||
| + | «[[LambertW.cin]]», |
||
| + | «[[Tania.cin]]» |
||
| + | |||
| + | «[[Applied Mathematical Sciences]]», |
||
| + | «[[Lambert Academic Publishing]]», |
||
| + | «[[Logarithm]]», |
||
| + | «[[Superfunction]]», |
||
| + | «[[Superfunctions]]», |
||
| + | «[[SuTra]]», |
||
| + | «[[SuZex]]», |
||
| + | «[[Tania function]]», |
||
| + | «[[Zex]]», |
||
| + | |||
| + | «[[Суперфункции]]», |
||
| + | |||
| + | [[Category:Applied Mathematical Sciences]] |
||
| + | [[Category:Book]] |
||
| + | [[Category:BookPlot]] |
||
| + | [[Category:C++]] |
||
| + | [[Category:Explicit plot]] |
||
| + | [[Category:Latex]] |
||
| + | [[Category:Lambert Academic Publishing]] |
||
| + | [[Category:SuTra]] |
||
| + | [[Category:Trappmann function]] |
||
| + | [[Category:Superfunction]] |
||
| + | [[Category:Superfunctions]] |
||
Latest revision as of 21:55, 7 January 2026
Fig.20.5 from page 276 of book of «Superfunctions»[1], 2020.
The image is used also as Рис.20.5 at page 284 of the Russian version «Суперфункции» [2], 2014.
The figure shows the explicit plot of function SuTra and its asymptotic \( x \mapsto -\ln(-x)\).
The additional horizontal gridline shows \(1\!+\!\mathrm e=\mathrm{SuTra}(2)\)
SuTra is superfunction of the Trappmann function \(\mathrm{tra} = z \mapsto z+\mathrm e^z\).
Function SuTra satisfies the Transfer equation
\(\mathrm{tra}(\mathrm{SuTra}(z))=\mathrm{SuTra}(z+1) \)
Here, the Trappmann function \(\mathrm{tra}\) is treated as a Transfer function.
Until year 2013, function SuTra had been believed to be difficult to evaluate (if at al) as the
Trappmann function has no fixed point.
However, after to guess the asymptotic behavior (thin curve in the explicit plot), the evaluation of SuTra becomes straightforward.
It is described at Applied Mathematical Sciences [3], 2013.
To year 2026, function \(z \mapsto -\mathrm{ZuZex}(-z)\)
seems to be the only reported entire function with logarithmic asymptotic.
C++ generator of curves
/* Files ado.cin, SuZex.cin, LambertW.cin and Tania.cin sould be loaded to the working directory in order to compile the C++ code below */
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include<complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "Tania.cin" // need for LambertW
#include "LambertW.cin" // need for AuZex
#include "SuZex.cin"
//#include "AuZex.cin"
z_type tra(z_type z){ return exp(z)+z;}
//z_type F(z_type z){ return log(suzex(z));}
//z_type G(z_type z){ return auzex(exp(z));}
z_type sutra(z_type z){ if( Re(z)<2. || fabs(Im(z))>2. ) return log(suzex(z));
return tra(sutra(z-1.));}
#include "ado.cin"
#define M(x,y) fprintf(o,"%6.4f %6.4f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%6.4f %6.4f L\n",0.+x,0.+y);
main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d; FILE *o;o=fopen("SuTraPlo3.eps","w"); ado(o,604,812);
fprintf(o,"302 202 translate\n 100 100 scale\n");
fprintf(o,"1 setlinejoin 2 setlinecap\n");
for(n=-2;n<7;n++) {M(-3,n)L(3,n)}
for(m=-3;m<4;m++) {M(m,-2)L(m,6)}
// M(M_E,0)L(M_E,1) M(0,M_E)L(1,M_E)
M(0,1.+M_E) L(2,1.+M_E)
fprintf(o,".004 W S\n");
// DO(m,700){x=.01 +.02*m; y=Re(LambertW(LambertW(x)));if(m==0) M(x,y) else L(x,y) if(x>12.03||y>12.03) break;} fprintf(o,".033 W 1 0 0 RGB S\n");
// DO(m,700){x=.01 +.02*m; y=Re(LambertW(x));if(m==0) M(x,y) else L(x,y) if(x>12.03||y>12.03) break;} fprintf(o,".04 W 1 .5 0 RGB S\n");
// M(0,0) L(12.03,12.03) fprintf(o,".04 W 0 1 0 RGB S\n");
DO(m,700){x=-5.02 +.02*m; y=Re(sutra(x)); if(m==0) M(x,y) else L(x,y) if(x>3.03||y>6.1) break;} fprintf(o,".03 W 0 0 1 RGB S\n");
DO(m,240){x=-5.02 +.02*m; y=-log(-x); if(m==0) M(x,y) else L(x,y) if(x>3.03||y>6.03) break;} fprintf(o,".01 W .5 0 0 RGB S\n");
fprintf(o,"showpage\n"); fprintf(o,"%c%cTrailer\n",'%','%'); fclose(o);
system("epstopdf SuTraPlo3.eps");
system( "open SuTraPlo3.pdf"); //for macintosh
getchar(); system("killall Preview"); // For macintosh
}
Latex generator of labels
% file SuTraPlo3.pdf should be generated with the code above in order to compile the Latex document below. % Copyleft 2012 by Dmitrii Kouznetsov
\documentclass[12pt]{article}
\usepackage{geometry}
\usepackage{graphicx}
\usepackage{rotating}
\paperwidth 608pt
\paperheight 816pt
\topmargin -98pt
\oddsidemargin -71pt
\textwidth 900pt
\textheight 900pt
\pagestyle {empty}
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \ing {\includegraphics}
\parindent 0pt
\pagestyle{empty}
\begin{document}
\begin{picture}(602,805)
\put(310,794){\sx{4}{$y$}}
\put(220,566){\sx{3.8}{$1\!+\!\mathrm e$}}
\put(310,690){\sx{4}{$5$}}
\put(310,590){\sx{4}{$4$}}
\put(310,490){\sx{4}{$3$}}
\put(310,390){\sx{4}{$2$}}
\put(310,289){\sx{4}{$1$}}
\put(312,187){\sx{4}{$0$}}
\put(290, 87){\sx{4}{$-\!1$}}
%\put(325,098){\sx{4}{$0$}}
\put(068,206){\sx{4}{$-\!2$}}
\put(168,206){\sx{4}{$-\!1$}}
\put(291,206){\sx{4}{$0$}}
\put(392,206){\sx{4}{$1$}}
\put(492,206){\sx{4}{$2$}}
\put(578,206){\sx{4}{$x$}}
\put(462,308){\sx{4.2}{\rot{70}$y\!=\!\mathrm{SuTra}(x)$\ero}}
\put(44,314){\sx{3.8}{\rot{0}$y\!=\!-\!\ln(-\!x)$\ero}}
%\put(10,10){\ing{ExpQ2plot}}
%\put(10,10){\ing{SuZexPlot511}}
\put(0,0){\ing{SuTraplo3}}
%\put(0,0){\ing{SuTraplo3}}
\end{picture}
\end{document}
References
- ↑ https://mizugadro.mydns.jp/BOOK/468.pdf D.Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.
- ↑
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
https://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014 - ↑
https://www.m-hikari.com/ams/ams-2013/ams-129-132-2013/kouznetsovAMS129-132-2013.pdf
https://mizugadro.mydns.jp/PAPERS/2013hikari.pdf D.Kouznetsov. Entire Function with Logarithmic Asymptotic. Applied Mathematical Sciences, Vol. 7, 2013, no. 131, 6527 - 6541
Keywords
«ado.cin», «SuZex.cin», «LambertW.cin», «Tania.cin»
«Applied Mathematical Sciences», «Lambert Academic Publishing», «Logarithm», «Superfunction», «Superfunctions», «SuTra», «SuZex», «Tania function», «Zex»,
«Суперфункции»,
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 17:50, 20 June 2013 | 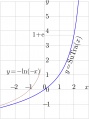 | 1,262 × 1,694 (182 KB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
The following page uses this file: