Difference between revisions of "File:Sqrt2srav.png"

Revision as of 22:32, 30 December 2025

Fig.16.8 from page 230 of book «Superfunctions»^[1], 2020.

It appears also as Рис.16.9 at page 234 of the Russian version «Суперфункции»^[2], 2015

This image is used also in article ^[3] at Mathemarics of Compitation, 2010.

The figure shows the comparison or two half iterate of exponential to base \( \sqrt{2} \) constructed at fixed point 2 and at fixed point 4.

\( y=\exp_{\sqrt{2},4}^{~1/2}(x) \) , solid line

\( y=\exp_{\sqrt{2},2}^{~1/2}(x) \) , dashed line

The second number in the subscript indicates the fixed point used to perform the regular iterate for the evaluation.

The thin curve represents the difference, \(y=D(x)= \exp_{\sqrt{2},\mathrm 4}^{~1/2}(x) -\exp_{\sqrt{2},\mathrm 2}^{~1/2}(x)\) , scaled with factor \(10^{24} \).

Description

The half iterate of a transfer function \(T\) is such function \(\varphi\) that \[ \varphi(\varphi(z))=T(z) \] It is special case of the \(n\)th iterate of the transfer function with \(n=1/2\).

For \(T=\exp\), such an function had been announced in 1950 by Hellmuth Knezer ^[4] in 1950 and implemented ^[5]^[6] in 2009, 2010; it satisfies equation \(\varphi(\varphi(z))=\mathrm e^z\).

For general case, the \(n\) iterate of a transfer function \(T\) is expressed through its superfunction \(F\) and its abelfunction \(G=F^{-1}\) as follows: \[ T^n(z)=F(n+G(z)) \] Here, number \(n\) of the iterate has no need to be integer.

The picture corresponds to \(T(z)=\exp_{\sqrt{2}}(z)=\exp(z/2) \).

The superfunction is not unique. The two growing real-holomorphic superexponentials are used:

\(F=\mathrm{SuExp}_{\sqrt{2},1}=\mathrm{tet}_{\sqrt{2}}\) and

\(F=\mathrm{SuExp}_{\sqrt{2},3}\)

The second number in the subscript indicates the value of the superfunction at zero.

For real values of the argument, the first superexponential (tetration base \(\sqrt{2}\)) gives the halfiterate \(T^{1/2}(x)\) that is valid for \(x<4\). The second superexponential gives the halfiterate \(T^{1/2}(x)\) that is valid for \(x>2\).

In the range \(2<x<4\), these two half iterates look very similar; the deviation is smaller than \(10^{-24}\).
In order to show this deviation in the picture, it is scaled with factor \(10^{24}\).

Feel free to look at the book cited for the more detailed description and/or download the code below to reproduce and/or to modify the picture.
At the reuse, attribute the source and indicate the modification(s) in the code, if any.

Please communicate Editor if you see any misprint, mistake, error in the Book, in the picture and/or in its description.

C++ generator of the curves

/* Files ado.cin, sqrt2f23e.cin, sqrt2f23l.cin, sqrt2f43e.cin, sqrt2f43l.cin should be loaded in order to compile the code below.*/

 #include <math.h>
 #include <stdio.h>
 #include <stdlib.h>
 #define DB double
 #define DO(x,y) for(x=0;x<y;x++)
 #include <complex>
 typedef std::complex<double> z_type;
 #define Re(x) x.real()
 #define Im(x) x.imag()
 #define I z_type(0.,1.)
// #include "conto.cin"
#include "ado.cin"
 #include "sqrt2f23E.cin"
 #include "sqrt2f23L.cin"
 #include "sqrt2f43E.cin"
 #include "sqrt2f43L.cin"
// #include "superex.cin"
// #include "slog14128.cin"

// #include "exq.cin"
z_type exq(z_type z){   DB T4= 19.236149042042854712;
                        DB T2=-17.143148179354847104;   z_type z3=z-3.;
//      return 2.47e-25*(z-2.)*(4.-z)*(1.+z3*(.122+z3*.009))*sin(0.75+z3*(-.0767+z3*(+.01) )+ T4*log(4.-z) + T2*log(z-2.) );
//      return 2.47e-25*(z-2.)*(4.-z)*(1.+z3*(.122+z3*.009))*sin(0.75+z3*(-.075+z3*(+.01) )+ T4*log(4.-z) + T2*log(z-2.) );
//      return 2.47e-25*(z-2.)*(4.-z)*(1.+z3*(.122+z3*.006))*sin(0.74+z3*(-.07+z3*(+.01) )+ T4*log(4.-z) + T2*log(z-2.) );
//      return 2.48e-25*(z-2.)*(4.-z)*(1.+z3*(.120+z3*.006))*sin(0.747+z3*(-.069+z3*(+.007) )+ T4*log(4.-z) + T2*log(z-2.) );

//      return 2.48e-25*(z-2.)*(4.-z)*(1.+z3*(.120+z3*.006))*sin(0.747+z3*(-.068+z3*(+.007) )+ T4*log(4.-z) + T2*log(z-2.) );
//      return 2.48e-25*(z-2.)*(4.-z)*(1.+z3*(.120+z3*.006))*sin(0.4+z3*(-.067+z3*(-.8) )+ T4*log(4.-z) + T2*log(z-2.) );
//      return 2.48e-25*(z-2.)*(4.-z)*(1.+z3*(.120+z3*.006))*sin(0.4+z3*(-.067+z3*(-.8) )+ T4*log(4.-z) + T2*log(z-2.) );
//      return 2.48e-25*(z-2.)*(4.-z)*(1.+z3*(.120+z3*.006))*sin(0.4+z3*(-.07+z3*(-.8) )+ T4*log(4.-z) + T2*log(z-2.) );
        return 2.48e-25*(z-2.)*(4.-z)*(1.+z3*(.120+z3*.006))*sin(0.4+z3*(-.08+z3*(-.8) )+ T4*log(4.-z) + T2*log(z-2.) );
                }


DB XI[200]={
2.00, 2.01, 2.02, 2.03, 2.04, 2.05, 2.06, 2.07, 2.08, 2.09, 2.10, 2.11, 2.12, 2.13, 2.14, 2.15, 2.16, 2.17, 2.18, 2.19,
2.20, 2.21, 2.22, 2.23, 2.24, 2.25, 2.26, 2.27, 2.28, 2.29, 2.30, 2.31, 2.32, 2.33, 2.34, 2.35, 2.36, 2.37, 2.38, 2.39,
2.40, 2.41, 2.42, 2.43, 2.44, 2.45, 2.46, 2.47, 2.48, 2.49, 2.50, 2.51, 2.52, 2.53, 2.54, 2.55, 2.56, 2.57, 2.58, 2.59,
2.60, 2.61, 2.62, 2.63, 2.64, 2.65, 2.66, 2.67, 2.68, 2.69, 2.70, 2.71, 2.72, 2.73, 2.74, 2.75, 2.76, 2.77, 2.78, 2.79,
2.80, 2.81, 2.82, 2.83, 2.84, 2.85, 2.86, 2.87, 2.88, 2.89, 2.90, 2.91, 2.92, 2.93, 2.94, 2.95, 2.96, 2.97, 2.98, 2.99,
3.00, 3.01, 3.02, 3.03, 3.04, 3.05, 3.06, 3.07, 3.08, 3.09, 3.10, 3.11, 3.12, 3.13, 3.14, 3.15, 3.16, 3.17, 3.18, 3.19,
3.20, 3.21, 3.22, 3.23, 3.24, 3.25, 3.26, 3.27, 3.28, 3.29, 3.30, 3.31, 3.32, 3.33, 3.34, 3.35, 3.36, 3.37, 3.38, 3.39,
3.40, 3.41, 3.42, 3.43, 3.44, 3.45, 3.46, 3.47, 3.48, 3.49, 3.50, 3.51, 3.52, 3.53, 3.54, 3.55, 3.56, 3.57, 3.58, 3.59,
3.60, 3.61, 3.62, 3.63, 3.64, 3.65, 3.66, 3.67, 3.68, 3.69, 3.70, 3.71, 3.72, 3.73, 3.74, 3.75, 3.76, 3.77, 3.78, 3.79,
3.80, 3.81, 3.82, 3.83, 3.84, 3.85, 3.86, 3.87, 3.88, 3.89, 3.90, 3.91, 3.92, 3.93, 3.94, 3.95, 3.96, 3.97, 3.98, 3.99};

//seq(10000000000000000000000000 eq42i[i], i = 1 .. 199) // multiply the table below with 10^25
DB DI[200]={0.,
 0.4784698105   -0.05393190341, -0.1300677822,  -0.03171912709, 0.1785649091, 
-0.2250109272,  0.1825902914,   0.03480286362,  -0.3467282069,  0.3008735706, 
 0.2712188539,  -0.4190409114,  -0.3490350151,  0.3694646591,   0.5766896417, 
-0.02558065033, -0.6509275876,  -0.5677290067,  0.1249427107,   0.7445345668, 
 0.7404203400,  0.1276956912,   -0.6160794452,  -0.9628063538,  -0.6916022303, 
 0.01864447876, 0.7488833086,   1.101226313,    0.9014321358,   0.2561118946, 
-0.5300917829,  -1.110965026,   -1.247875232,   -0.8932436694,  -0.1889188837, 
 0.6042806729,  1.208925529,    1.425359378,    1.188972596,    0.5785454907, 
-0.2192350209,  -0.9722698076,  -1.471223669,   -1.584225579,   -1.285665934, 
-0.6552228513,  0.1488558485,   0.9326874399,   1.514042501,    1.762841619, 
 1.626741407,   1.137951659,    0.4018211902,   -0.4286446672,  -1.185893868, 
-1.721405217,   -1.933299208,   -1.783360064,   -1.301259878,   -0.5762799943, 
 0.2610215297,  1.063258680,    1.692178857,    2.041693575,    2.054394851, 
 1.729315148,   1.120250436,    0.3254866584,   -0.5289731871,  -1.309749251,
-1.896727084,   -2.200905751,   -2.176957263,   -1.828915204,   -1.208481545, 
-0.4065111531,  0.4608414413,   1.269162309,    1.903518088,    2.274423794, 
 2.329910221,   2.062170481,    1.508044374,    0.7434411090,   -0.1274043434, 
-0.9862966412,  -1.717093805,   -2.221232577,   -2.430741451,   -2.317083136, 
-1.894734068,   -1.219099562,   -0.3790914522,  0.5146293821,   1.344202005, 
 2.000019677,   2.395098433,    2.476513136,    2.232427985,    1.693805806, 
 0.9305534145,  0.04256669434,  -0.8532073059,  -1.638054138,   -2.207164096,
-2.483657197,   -2.429103975,   -2.049103493,   -1.393092023,   -0.5482898657, 
 0.3715392444,  1.241138307,    1.940691601,    2.372404168,    2.474456697, 
 2.230337845,   1.672108541,    0.8769280448,   -0.04292211556, -0.9553576726, 
-1.727182735,   -2.243596738,   -2.425705096,   -2.243353388,   -1.721136622, 
-0.9363222889,  -.008568273516, 0.9174331778,   1.694075610,    2.194493483, 
 2.334032812,   2.085879418,    1.487850807,    0.6385838664,   -0.3169989468, 
-1.211215472,   -1.882663464,   -2.205965842,   -2.116798723,   -1.627093624, 
-0.8266252487,  0.1305785338,   1.053731641,    1.752439170,    2.076719446, 
 1.951641871,   1.398412552,    0.5356620174,   -0.4416412943,  -1.303325066, 
-1.837659684,   -1.905696400,   -1.482410042,   -0.6719601817,  0.3107105811, 
 1.191600113,   1.712573743,    1.710469692,    1.176345414,    0.2724209897, 
-0.7061642661,  -1.421131980,   -1.609137760,   -1.188763710,   -0.3119998189, 
 0.6722631328,  1.345399787,    1.398988810,    0.7938478007,   -0.1863084618, 
-1.040543314,   -1.297193305,   -0.7929908943,  0.1807419873,   1.000006240, 
 1.091699572,   0.3698400463,   -0.6124347228,  -1.024247436,   -0.4742694444, 
 0.5137381025,  0.8869221813,   0.1975127230,   -0.6902438791,  -0.5357760631, 
 0.4270413342,  0.5566459653,   -0.3748406966,  -0.3814257507,  0.4878409640,
-0.08114350401, -0.2447048034,  0.3328830351,   -0.2984357129,  0.1840035673, 
 0.1664529435,  2.207054268,    341.6955295,    1.549459936e6 };
// I think, data are from Maple.
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
//FILE *o;o=fopen("fig09c.eps","w");  ado(o,124,82);
//  FILE *o;o=fopen("figexcr.eps","w");  ado(o,0,0,126,110);
//  FILE *o;o=fopen("sqrt26pl.eps","w");  ado(o,1260,810);
//  FILE *o;o=fopen("sqrt26sra.eps","w");  ado(o,660,210);
  FILE *o;o=fopen("sqrt2sra.eps","w");  ado(o,1240,810);
// fprintf(o,"62 12 translate\n 10 10 scale\n");
// fprintf(o,"64 30 translate\n 10 10 scale\n");
// fprintf(o,"620 120 translate\n 100 100 scale\n");
 fprintf(o,"620 110 translate\n 100 100 scale\n");
#define M(x,y) fprintf(o,"%7.4f %7.4f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%7.4f %7.4f L\n",0.+x,0.+y);
//#define o(x,y) fprintf(o,"%7.4f %7.4f o\n",0.+x,0.+y);

M(0,-1.1)L(0,6.6)
M(-6.1,0)L(6.1,0)
fprintf(o,".03 W S\n");
for(m=-6;m<7;m++){if(m!=0){M(m,-1)L(m,6)}}
for(n=-1;n<7;n++){if(n!=0){M(-6,n)L(6,n)}}
fprintf(o,".01 W S\n");

fprintf(o,"1 setlinejoin 0 setlinecap\n");

for(m=2;m<196;m++){ if(m==2) M(XI[m],.1*DI[m]) else L(XI[m],.1*DI[m]) } 
fprintf(o,"1 0 1 RGB S\n");
// No way to see any deviation at this resolution


for(m=0;m<42;m+=1){ x=2.001+.1*m; z=z_type(x,0.); 
//                      d=UQ2L(z); t=Re(d);  y=Re(UQ2E(.5+d));
                        d=F43L(z); t=Re(d);  y=Re(F43E(.5+d));
                //      printf("%6.3f %6.3f %6.3f\n",x,t,y); 
                        if(m==0) M(x,y) else L(x,y)}
fprintf(o,".03 W 0 0 1 RGB S\n");

for(m=0;m<104;m+=1){x=3.99-.1*m; z=x;
        //      z=TQ2L(z);y=Re(TQ2E(.5+z));
                z=F23L(z);y=Re(F23E(.5+z));
                 if(m/2*2==m) M(x,y) else L(x,y)}
fprintf(o,".06 W 1 0 0 RGB S\n");

DB T4= 19.236149042042854712;
DB T2=-17.143148179354847104;
for(m=0;m<500;m+=1){ x=2.002+.004*m; z=z_type(x,0.);
//                       c=UQ2L(z); p=Re(UQ2E(.5+c));
//                       d=TQ2L(z); q=Re(TQ2E(.5+d));
                        c=exq(z);  y=1.e24*Re(c);if(m==0) M(x,y) else L(x,y)}
fprintf(o,".005 W 0 .1 0 RGB S\n");

/* NATURAL SEXP
  // solid thin
DO(m,98){x=-6.2+.1*m; z=z_type(x,0.); d=FSLOG(z);y=Re(FSEXP(.5+d));  if(m==0) M(x,y) else L(x,y)}
fprintf(o,".01 W 0 0 0 RGB S\n");
*/

 fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
//      system(      "gv figexcr.eps &"); //for UNIX
//      system(    "open figexcr.eps"); //for macintosh
        system("epstopdf sqrt2sra.eps"); 
        system(    "open sqrt2sra.pdf"); //for LINUX 


//z=3.5;c=exq(z); printf("exq(3.5)=%19.4e %19.4e\n",Re(c),Im(c));
//z=3.;c=exq(z); printf("exq(3.0)=%19.4e %19.4e\n",Re(c),Im(c));
//      getchar(); system("killall Preview"); // For macintosh
}

Latex generator of the labels

\documentclass[12pt]{article} 
\usepackage{geometry} 
\usepackage{graphicx} 
\usepackage{rotating} 
\paperwidth 1230pt 
\paperheight 798pt 
\topmargin -100pt 
\oddsidemargin -75pt 
\textwidth 1640pt 
\textheight 1600pt 
\pagestyle {empty} 
\newcommand \sx {\scalebox} 
\newcommand \rot {\begin{rotate}} 
\newcommand \ero {\end{rotate}} 
\newcommand \ing {\includegraphics} 
\parindent 0pt
\pagestyle{empty} 
\begin{document} 

%\begin{picture}(360,740) 
\begin{picture}(1360,790) 
%\put(10,10){\ing{IterPowPlot}} 
%\put(40,40){\ing{Itereq2tlo}} 
%\put(0,0){\ing{sqrt26plo}} 
\put(0,0){\ing{sqrt2sra}} 
\put(590,767){\sx{4}{$y$}}
\put(590,697){\sx{4}{$6$}}
\put(590,597){\sx{4}{$5$}}
\put(590,497){\sx{4}{$4$}}
\put(590,396){\sx{4}{$3$}}
\put(590,296){\sx{4}{$2$}}
\put(590,196){\sx{4}{$1$}}
\put(590, 96){\sx{4}{$0$}}
\put(90,50){\sx{4}{$-5$}}
\put(180,50){\sx{4}{$-4$}}
\put(280,50){\sx{4}{$-3$}}
\put(380,50){\sx{4}{$-2$}}
\put(480,50){\sx{4}{$-1$}}
\put(612,50){\sx{4}{$0$}}
\put(712,50){\sx{4}{$1$}}
\put(812,50){\sx{4}{$2$}}
\put(912,50){\sx{4}{$3$}}
\put(1012,50){\sx{4}{$4$}}
\put(1112,50){\sx{4}{$5$}}
\put(1200,50){\sx{4}{$x$}}
\put(778,644){\sx{5}{$y\!=\!\exp_{\sqrt{2},4}^{~ 1/2}(x)$}}
\put(220,150){\sx{5}{$y\!=\!\exp_{\sqrt{2},2}^{~ 1/2}(x)$}}
\put(900,152){\sx{5}{$y\!=\!10^{24}D(x)$}}
\end{picture} 
\end{document}

Refereces

↑ https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.
↑ https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
http://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014.
↑ http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
http://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf offprint D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
↑ http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi Hellmuth Kneser. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen. Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67
↑ http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
D.Kouznetsov. (2009). Solutions of F(z+1)=exp(F(z)) in the complex plane. Mathematics of Computation, 78: 1647-1670. DOI:10.1090/S0025-5718-09-02188-7
↑ http://mizugadro.mydns.jp/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45

Keywords

«Abelexponential», «Abelfunction», «Arctetration», «Base sqrt2», «Book», «BookPlot», «Explicit plot», «Exponential», «Iterate half», «Iterate», «Mathematics of Computation», «Sledgehammer to crack a nut», «Superexponential», «Superfunction», «Superfunctions»,

«Суперфункции»,

File history

Click on a date/time to view the file as it appeared at that time.

	Date/Time	Thumbnail	Dimensions	User	Comment
current	06:14, 1 December 2018		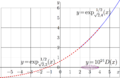2,532 × 1,639 (263 KB)	Maintenance script (talk \| contribs)	Importing image file

You cannot overwrite this file.

File usage

The following page uses this file:

Sledgehammer to crack a nut

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Horizontal resolution	590.55 dpc
Vertical resolution	590.55 dpc

[1] ttps://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.

[2] ttps://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
http://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014.

[3] ttp://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
http://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf offprint D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.

[k-4] ttp://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi Hellmuth Kneser. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen. Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67

[5] ttp://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
D.Kouznetsov. (2009). Solutions of F(z+1)=exp(F(z)) in the complex plane. Mathematics of Computation, 78: 1647-1670. DOI:10.1090/S0025-5718-09-02188-7

[6] ttp://mizugadro.mydns.jp/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45

[1]

[2]

[3]

[4]

[5]

[6]

@@ Line 1: / Line 1: @@
+{{oq|Sqrt2srav.png|Original file ‎(2,532 × 1,639 pixels, file size: 263 KB, MIME type: image/png)|400}}
-Comparison or two half iterate of exponent to base \( \sqrt{2} \) constructed at fixed point 2 and at fixed point 4.
+Fig.16.8 from page 230 of  book «[[Superfunctions]]»<ref>
-\( y=\exp_{\sqrt{2},\mathrm u}^{~1/2}(x) \) , solid line
+https://mizugadro.mydns.jp/BOOK/468.pdf
+Dmitrii Kouznetsov. [[Superfunctions]]. [[Lambert Academic Publishing]], 2020.
+</ref>, 2020.
+It appears also as Рис.16.9 at page 234 of the Russian version «[[Суперфункции]]»<ref>
-\( y=\exp_{\sqrt{2},\mathrm d}^{~1/2}(x) \) , dashed line
-The thin curve represents the difference,
-\(y=D(x)=
-\exp_{\sqrt{2},\mathrm u}^{~1/2}(x)
--\exp_{\sqrt{2},\mathrm d}^{~1/2}(x)\) ,
-scaled with factor \(10^{24} \).
-Usage: this is figure 16.9 of the book [[Суперфункции]] (2014, In Russian) <ref>
 https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 <br>
-http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf <br>
 http://mizugadro.mydns.jp/BOOK/202.pdf
 Д.Кузнецов. Суперфункции. [[Lambert Academic Publishing]], 2014.
-</ref>; the English version is in preparation in 2015.
+</ref>, 2015
 This image is used also in article
@@ Line 23: / Line 17: @@
 http://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf offprint
 D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
+</ref> at [[Mathemarics of Compitation]], 2010.
-</ref>.
+The figure shows the comparison or two half iterate of [[exponential]] to [[base sqrt2|base \( \sqrt{2} \)]] constructed at fixed point 2 and at fixed point 4.
+\( y=\exp_{\sqrt{2},4}^{~1/2}(x) \) , solid line
-==Refereces==
-<references/>
+\( y=\exp_{\sqrt{2},2}^{~1/2}(x) \) , dashed line
+The second number in the subscript indicates the [[fixed point]] used to perform the [[regular iterate]]
+for the evaluation.
+The thin curve represents the difference,
+\(y=D(x)=
+\exp_{\sqrt{2},\mathrm 4}^{~1/2}(x)
+-\exp_{\sqrt{2},\mathrm 2}^{~1/2}(x)\) ,
+scaled with factor \(10^{24} \).
+==Description==
+The half iterate of a [[transfer function]] \(T\) is such function  \(\varphi\) that
+\[
+\varphi(\varphi(z))=T(z)
+\]
+It is special case of the \(n\)th iterate of the transfer function with \(n=1/2\).
+For \(T=\exp\), such an function had been announced in 1950 by [[Hellmuth Knezer]]
+<ref name="k">
+http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi
+[[Hellmuth Kneser]]. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen.
+Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950)  / Artikel / 56 - 67
+</ref> in 1950 and implemented <ref>
+http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html <br>
+D.Kouznetsov. (2009). Solutions of F(z+1)=exp(F(z)) in the complex plane. [[Mathematics of Computation]], 78: 1647-1670. DOI:10.1090/S0025-5718-09-02188-7
+</ref><ref>
+http://mizugadro.mydns.jp/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. [[Vladikavkaz Mathematical Journal]], 2010, v.12, issue 2, p.31-45
+</ref> in 2009, 2010; it satisfies equation \(\varphi(\varphi(z))=\mathrm e^z\).
+For general case, the \(n\) iterate of a [[transfer function]] \(T\) is expressed through its [[superfunction]]
+\(F\) and its [[abelfunction]] \(G=F^{-1}\) as follows:
+\[
+T^n(z)=F(n+G(z))
+\]
+Here, number \(n\) of the iterate has no need to be integer.
+The picture corresponds to \(T(z)=\exp_{\sqrt{2}}(z)=\exp(z/2) \).
+The [[superfunction]] is not unique. The two growing real-holomorphic superexponentials are used:
+\(F=\mathrm{SuExp}_{\sqrt{2},1}=\mathrm{tet}_{\sqrt{2}}\) and
+\(F=\mathrm{SuExp}_{\sqrt{2},3}\)
+The second number in the subscript indicates the value of the superfunction at zero.
+For real values of the argument, the first [[superexponential]] (tetration base \(\sqrt{2}\))
+gives the halfiterate \(T^{1/2}(x)\) that is valid for \(x<4\).
+The second superexponential gives the halfiterate \(T^{1/2}(x)\) that is valid for \(x>2\).
+In the range \(2<x<4\), these two half iterates look very similar; the deviation is smaller than \(10^{-24}\).<br>
+In order to show this deviation in the picture, it is scaled with factor \(10^{24}\).
+Feel free to look at the book cited for the more detailed description and/or
+download the code below to reproduce and/or to modify the picture.<br>
+At the reuse, attribute the source and indicate the modification(s) in the code, if any.
+Please communicate Editor if you see any misprint, mistake, error in the Book, in the picture and/or
+in its description.
 ==[[C++]] generator of the curves==
-Files [[ado.cin]],
+/* Files [[ado.cin]],
-[[conto.cin]],
 [[sqrt2f23e.cin]],
 [[sqrt2f23l.cin]],
 [[sqrt2f43e.cin]],
 [[sqrt2f43l.cin]]
-should be loaded in order to compile the code below.
+should be loaded in order to compile the code below.*/
+<pre>
-<poem><nomathjax><nowiki>
  #include <math.h>
  #include <stdio.h>
@@ Line 197: / Line 248: @@
 //      getchar(); system("killall Preview"); // For macintosh
 }
+</pre>
-</nowiki></nomathjax></poem>
 ==[[Latex]] generator of the labels==
+<pre>
-<poem><nomathjax><nowiki>
 \documentclass[12pt]{article}
 \usepackage{geometry}
@@ Line 252: / Line 302: @@
 \end{picture}
 \end{document}
+</pre>
+==Refereces==
+{{ref}}
+{{fer}}
+==Keywords==
+«[[Abelexponential]]»,
+«[[Abelfunction]]»,
+«[[Arctetration]]»,
+«[[Base sqrt2]]»,
+«[[Book]]»,
+«[[BookPlot]]»,
+«[[Explicit plot]]»,
+«[[Exponential]]»,
+«[[Iterate half]]»,
+«[[Iterate]]»,
+«[[Mathematics of Computation]]»,
+«[[Sledgehammer to crack a nut]]»,
+«[[Superexponential]]»,
+«[[Superfunction]]»,
+«[[Superfunctions]]»,
+«[[Суперфункции]]»,
-</nowiki></nomathjax></poem>
+[[Category:Abelfunction]]
+[[Category:Arctetration]]
 [[Category:Base sqrt2]]
 [[Category:Book]]
@@ Line 260: / Line 335: @@
 [[Category:C++]]
 [[Category:Explicit plot]]
-[[Category:Exp]]
+[[Category:Exponential]]
 [[Category:Generator]]
 [[Category:Latex]]
+[[Category:Mathematics of Computation]]
+[[Category:Superexponential]]
 [[Category:Superfunction]]
+[[Category:Superfunctions]]
 [[Category:Tetration]]