Difference between revisions of "Entire Function with Logarithmic Asymptotic"
(add pics) |
(→Keywords: and categories) |
||
| Line 73: | Line 73: | ||
==Keywords== |
==Keywords== |
||
| + | |||
| ⚫ | |||
| + | «[[Tania.cin]]», |
||
| + | «[[LambertW.cin]]», |
||
| + | «[[SuZex.cin]]», |
||
| ⚫ | |||
| + | «[[Logarithm]]», |
||
| + | «[[Superfunctions]]», |
||
| + | «[[SuTra]]», |
||
| + | «[[Trappmann function]]», |
||
| + | |||
| + | [[Category:C++]] |
||
| + | [[Category:Complex map]] |
||
| + | [[Category:Entire Function with Logarithmic Asymptotic]] |
||
| + | [[Category:Logarithm]] |
||
| + | [[Category:Superfunctions]] |
||
| + | [[Category:Trappmann function]] |
||
Revision as of 15:51, 9 January 2026
Term Entire Function with Logarithmic Asymptotic appears as title of publication [1] at Applied Mathematical Sciences, 2013.
Term Entire Function with Logarithmic Asymptotic can make an impression of an oxymoron:
function logarithm has cut line, that cannot be reproduced with an entire function.
Term Entire Function with Logarithmic Asymptotic
refers to the sectorial asymptotic:
in some sector with vertex at the origin,
the function grows in a way, similar to that of Logarithm.
This sector cannot include the negative part of the real axis: there, the Logarithm is not a continuous function.
However the sector may cover almost all the complex plane, excluding an arbitrary narrow sector along the negative part of the real axis.
Definition
Entire Function with Logarithmic Asymptotic is function \(\Phi\) of complex argument such that
(1) \(\Phi\) is holomorphic in the whole complex plane
(2) in some sector of the complex plane \(\Phi\) approach function Logarithm, id est, there exist real values \(t_1\) and \(t_2\) such that \(-\pi<t_1<t_2<\pi\) and for any fixed real \(t\) with \(t_1<t<t_2\) , \[ \lim_{r \to +\infty} \Big( \Phi(r\exp(\mathrm i t)) - \log(r\exp(\mathrm i t)) \Big) = 0 \]
Superfunctions
The example [1] of an Entire Function with Logarithmic Asymptotic is described also in book "Superfunctions" [2][3].
The Entire Function with Logarithmic Asymptotic is expressed through the Superfunction SuTra of the elementary Trappmann function \(\mathrm{tra} = z \mapsto z+\exp(z) \):
\[
\Phi(z) = - \mathrm{SuTra} (-z)
\]
The complex map of Logarithm and that of function \(\Phi\) above are shown in the pictures below.
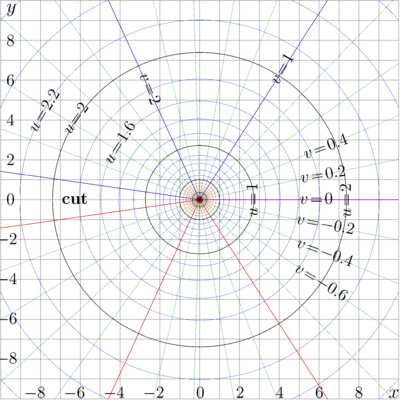
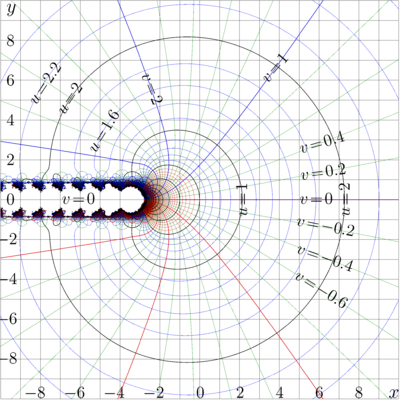
The maps above show function \(f(x\!+\!\mathrm i y) = u + \mathrm i v\ \) with
lines \(u=\rm const \) and
lines \(v=\rm const \)
in the \(x,y\) plane for \(f\!=\!\log\) and for \(f\!=\!\Phi \).
Acknowledgement
This article is created following the advice by ChatGPT.
References
- ↑ 1.0 1.1
https://www.m-hikari.com/ams/ams-2013/ams-129-132-2013/kouznetsovAMS129-132-2013.pdf
https://mizugadro.mydns.jp/PAPERS/2013hikari.pdf D.Kouznetsov. Entire Function with Logarithmic Asymptotic. Applied Mathematical Sciences, Vol. 7, 2013, no. 131, 6527 - 6541 - ↑
https://www.amazon.com/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862
https://mizugadro.mydns.jp/BOOK/468.pdf D.Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020. - ↑
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
https://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014 (In Russian)
Keywords
«Tania.cin», «LambertW.cin», «SuZex.cin», «Entire Function with Logarithmic Asymptotic», «Logarithm», «Superfunctions», «SuTra», «Trappmann function»,