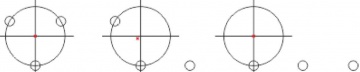
Varipend3
Varipend3 is mechanical device, suggested by Sergei Butov, with pretension to violate the First law of Newton [1], in the simplest configuration with 3 elementary bodies.
In varipend, the violation of the Laws of Newton is not so hidden as it is in the complicated intertioids developed in the Khrunichev center (that, according to publications about gravitsapa, involve high voltage discharge, evaporation of teflon and rotation of liquid by the special trajectory resembling tornado). For this case, the consideration of varipend with 3 bodies is loaded at TORI. The deduction is expected to be useful excersise for the first-grade students who begin to learn the Classical mechanics.
In the simulations by Butov, the external force is assumed; so, for the isolated system, the consideration by S.Butov is just wrong. The corrected deduction is suggested below. Any indications to errors (if any) or relative comments should be appreciated.
Introduction and notations
The problem comes from the idea of construction of a device that pulls itself by some internal forces that move some masses inside. S.Butov calls such a device "varipend" \cite{varipend}. The consideration presented in the original work implies that some external forces provide the movement of the elementary bodies inside by the circular trajectories until they are released. From the point of view of an isolated device, that consideration is just wrong. In this article, the simplest case of isolated varipend with 3 elementary bodies is considered.
Let three elementary bodies (Body0, Body1 and Body2) are connected with 3 ideal cords of unit length, in such a way, that initially the cords form a perfect triangle rotating in the plane with angular velocity \(\omega\) with main velocity 0 and main coordinate 0. At time \(t\!=\!0\) the 0-th elementary body passes the lowest part of its trajectory; and at this moment, the two cords that connect it with elementary body 1 and elementary body 2 are removed (cut); so, the 0th body remain free. However elementary body 2 and elementary body 3 are still connected with the ideal cord of length unity. The elimination (cutting) or cords affects neither position, nor velocities of the bodies. (However, it affects their accelerations).
Assignment: under the assumptions above, write out the simple explicit expressions for the coordinates and velocities of the bodies and that for the position of the center of mass.
Notations and case \(t\le 0\)
Numerate the bodies beginning with zero. Then, for moment of time \(t\!\le\!0\), the Cartesian coordinates \(X_n=X_n(t)\) and \(Y_n=Y_n(t)\) for \(n=0,1,2\) can be written as follows:
- \( \!\!\!\!\!\!\!\!\!(01) ~ ~ ~ \displaystyle X_n=\frac{1}{\sqrt{3}} \sin\!\left(\omega t + \frac{2 \pi}{3} n\right) ~\), \(~ \displaystyle Y_n=\frac{-1}{\sqrt{3}} \cos\!\left(\omega t + \frac{2 \pi}{3} n\right) ~\)
The components of velocities \(U_n=U_n(t)=X_n'(t)\) and \(U_n=U_n(t)=X_n'(t)\) for \(n=0,1,2\) can be expressed as follows:
- \( \!\!\!\!\!\!\!\!\!(01) ~ ~ ~ \displaystyle U_n(t)=\frac{\omega}{\sqrt{3}} \cos\!\left(\omega t + \frac{2 \pi}{3} n\right) ~\), \(~ \displaystyle V_n(t)=\frac{\omega}{\sqrt{3}} \sin\!\left(\omega t + \frac{2 \pi}{3} n\right) ~\)
The expressions above are valid for \(t\!\le\! 0\). At \(t \! = \! 0\),
- \( \!\!\!\!\!\!\!\!\!(03) ~ ~ ~ \displaystyle X_n(0)=\frac{\omega}{\sqrt{3}} \sin\!\left(\frac{2 \pi}{3} n\right) ~\), \(~ \displaystyle Y_n(0)=\frac{-\omega}{\sqrt{3}} \cos\!\left(\frac{2 \pi}{3} n\right) ~\)
- \( \!\!\!\!\!\!\!\!\!(04) ~ ~ ~ \displaystyle ~ ~ ~ U_n(0)=\frac{\omega}{\sqrt{3}} \cos\!\left(\frac{2 \pi}{3} n\right) ~\), \(~ \displaystyle V_n(0)=\frac{\omega}{\sqrt{3}} \sin\!\left(\frac{2 \pi}{3} n\right) ~\)
In particular,
- \( \!\!\!\!\!\!\!\!\!(05) ~ ~ ~ \displaystyle X_0(0)=0 ~\), \(~ \displaystyle Y_0(0)=\frac{-1}{\sqrt{3}} ~ ~\);
- \( \!\!\!\!\!\!\!\!\!(06) ~ ~ ~ \displaystyle X_1(0)=\frac{1}{\sqrt{3}} ~\), \(~ \displaystyle Y_1(0)=\frac{1}{2\sqrt{3}} ~ ~\);
- \( \!\!\!\!\!\!\!\!\!(07) ~ ~ ~ \displaystyle X_2(0)=\frac{-1}{\sqrt{3}} ~\), \(~ \displaystyle Y_2(0)=\frac{1}{2\sqrt{3}} ~ ~\);
Then
- \( \!\!\!\!\!\!\!\!\!(08) ~ ~ ~ \displaystyle U_0(0)=\frac{\omega}{\sqrt{3}} ~\), \(~ \displaystyle V_0(0)=0 ~ ~\);
- \( \!\!\!\!\!\!\!\!\! (09) ~ ~ ~ \displaystyle U_1(0)=\frac{-\omega}{2\sqrt{3}} ~\), \(~ \displaystyle V_1(0)=\frac{\omega}{2} ~ ~\);
- \( \!\!\!\!\!\!\!\!\! (10) ~ ~ ~ \displaystyle U_2(0)=\frac{-\omega}{2\sqrt{3}} ~\), \(~ \displaystyle V_2(0)=-\frac{\omega}{2} ~ ~\);
Case \(t\ge 0\)
According to the Introduction, at \(t\!=\!0\), the 0th particle becomes free. This means that
- \( \!\!\!\!\!\!\!\!\!(11) ~ ~ ~ \displaystyle U_0(t)=X_0'(t)=U_0(0)=\frac{\omega}{\sqrt{3}}~\), \(~ \displaystyle V_0(t)=Y_0'(t)=0\).
Integration of the equations above with initial conditions \(X_0(0)=0\), \(Y_0(0)=-1/\sqrt{3}\) gives
- \( \!\!\!\!\!\!\!\!\!(12) ~ ~ ~ \displaystyle X_0(t)=\frac{\omega}{\sqrt{3}}~ t ~ ~\), \(\displaystyle ~Y_0(t)=\frac{-1}{\sqrt{3}}\)
For the consideration of system of bodies 1 and 2 (that is isolated at \(t\!>\!0\)) , consider the system of coordinates that moves together with its center of mass. Let
- \( \!\!\!\!\!\!\!\!\!(13) ~ ~ ~ x_1(t)=X_1(t)-U_1(0)t ~\), \( ~ ~ y_1(t)=Y_1(t) ~\);
- \( \!\!\!\!\!\!\!\!\!(14) ~ ~ ~ x_2(t)=X_2(t)-U_1(0)t ~\), \( ~ ~ y_2(t)=Y_2(t) ~\)
Note that \(\displaystyle U_1(0)=U_2(0)=\frac{-\omega}{2 \sqrt{3}}\). Initial velocities in the new system of coordinates are
- \( \!\!\!\!\!\!\!\!\!(15) ~ ~ ~ u_1(0)=0 ~\), \( ~ ~ v_1(0)=V_1(0) = {\omega}/{2} ~\);
- \( \!\!\!\!\!\!\!\!\!(16) ~ ~ ~ u_2(0)=0 ~\), \( ~ ~ v_2(0)=V_2(0)= - {\omega}/{2}~\)
Evolution of isolated rotator is supposed to be well known; the solution is
- \( \!\!\!\!\!\!\!\!\!(17) ~ ~ ~ \displaystyle x_1(t)=\frac{1}{2} \cos(\omega t)~\), \(~\displaystyle y_1(t)=\frac{1}{2} \sin(\omega t)\)
- \( \!\!\!\!\!\!\!\!\!(18) ~ ~ ~ \displaystyle x_2(t)=\frac{-1}{2} \cos(\omega t)~\), \(~\displaystyle y_2(t)=\frac{-1}{2} \sin(\omega t)\)
Changing for the initial system of coordinate, we find
- \( \!\!\!\!\!\!\!\!\!(19) ~ ~ ~ \displaystyle X_1(t)=\frac{-\omega}{2 \sqrt{3}} t+\frac{1}{2} \cos(\omega t)~\), \(~\displaystyle Y_1(t)=\frac{1}{2 \sqrt{3}}+\frac{1}{2} \sin(\omega t)\)
- \( \!\!\!\!\!\!\!\!\!(20) ~ ~ ~ \displaystyle X_2(t)=\frac{-\omega}{2 \sqrt{3}} t - \frac{1}{2} \cos(\omega t)~\), \(~\displaystyle Y_2(t)=\frac{1}{2 \sqrt{3}} - \frac{1}{2} \sin(\omega t)\)
Conclusion
The accurate solution for the simplest case of isolated varipend with 3 elementary bodies is considered; explicit representation for all the coordinates in terms of elementary functions are suggested. Note that the couple (First and Second bodies) rotates with the same angular velocity \(\omega\), as the initial triad.
The center of mass of the system of all three bodies remains at the center of coordinates; one could expect this from the First Law of Newton. However, the cut of the last cord (between the First and Second bodies) also does not affect the trajectory of the center of mass. Consideration of cut of the cord between two bodies in a simple rotator is supposed to be performed by readers.
References
- ↑ http://varipend.narod.ru/index.html С.В.Бутов. Варипенд. О возможности безопорного перемещения. (2006).
Keywords
Sergei Butov, Varipend, Inertioids, First Law of Newton, Gravitsapa, Classical mechanics, Mathematics