File:SuTraMapT.jpg

File
File history
File usage
Metadata

Size of this preview: 600 × 600 pixels. Other resolutions: 240 × 240 pixels | 4,176 × 4,176 pixels.

Original file ‎(4,176 × 4,176 pixels, file size: 1.76 MB, MIME type: image/jpeg)

Fig.20.6 from page 279 of book «Superfunctions»^[1], 2020.

The image is used also as Рис.20.6 at page 288 of the Russian version «Суперфункции» ^[2], 2014.

The same image appears also as Figure 2 at page 6538 of the publication ^[3] at Applied Mathematical Sciences, 2013.

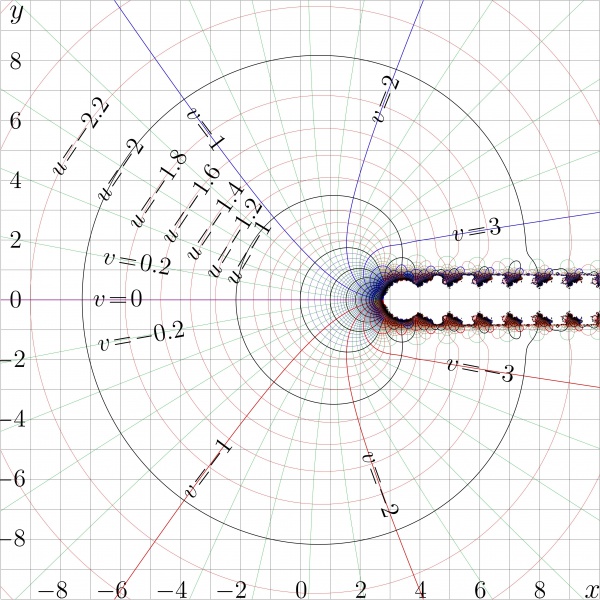
The figure shows the complex map of function SuTra; it is superfunction of the Trappmann function, \(\mathrm{tra}(z)\!=\!z\!+\!\exp(z)\).

In the figure, \[ u\!+\!\mathrm i v\!=\! \mathrm{SuTra}(x\!+\!\mathrm i y) \]

ChatGPT helped to improve the description below.

Description

The Trappmann function \(\mathrm{tra}\) is defined with \[ \mathrm{tra}(z) = z + \exp(z) \] By definition, it is elementary function and it is entire function.

Here, function tra is interpreted as a transfer function.

The Trappmann function has no fixed points.
The fixed points are important in construction of a superfunction as limiting, asymptotic values of the superfunctions. The specification of the asymptotic behavior of the superfunction gives way to its efficient (fast and precise) evaluation. A function without fixed points had been believed especially difficult, if at all, to construct its superfunction.
Such a believe lasted, roughly, until year 2013; then, the superfunction SuTra had been constructed and published ^[3].

The superfunction \(F\) is solution of the transfer equation \[ \mathrm{tra}(F(z))=F(z+1) \] In order to construct a simple superfunction, the additional condiction is applied:

\( F(z) \sim -\ln(-z) \) for large negative \( \Re(z) \)

These conditions allow to construct the asymptotic expansion for \(F(z)\); the truncated expansion appear as some slow function divided by \(z^m\); this truncated expansion is denoted as \(F_m(z) \).

The superfunction \(F\) appears as \[ F(z) = \lim_{M \to \infty} \mathrm{tra}^M( F_m(z-M) ) \]

Then \(\mathrm{SuTra}(z) = F(z+x_0) \)

where \(x_0\) is soliton of equation \(F(x_0)=0\) .

The resulting function has logarithmic asymptotic.

Let \( \Phi(z)= - \mathrm{SuTra}(- z) \)

Then, for any fixed real \(t\) with \(-\pi<t<\pi\) , \[ \lim_{r \to +\infty} \Big( \Phi(r\exp(\mathrm i t)) - \log(r\exp(\mathrm i t)) \Big) = 0 \]

Functions SuTra and \(\Phi\) have no singularities, and function \(\Phi\) mimics the behavior of Logarithm everywhere except the strip along its cut, id est, along the vicinity of the negative part of the real axis. There, the strong oscillations and (at along the negative part of the Real axis) huge values take place.

In such a way, function SuTra appears as Entire Function with Logarithmic Asymptotic:

\( -\mathrm{SuTra}(-z) \sim \log(z) \)

at large values of \(z\), while either \( \Re(z) \to +\infty \) or \( \Im(z) \to \pm \infty \)

Note

To year 2026, the logarithmic asymptotic of function SuTra mentioned above appears as a conjecture that follows from the set of numerical tests.

Due to the permanent attacks on the server Mizugadro (perhaps by KGB) and lack of the financial/technical support, Editor has no time to convert the conjecture to the theorem. The colleges, who are not under the attack, are invited to do it.

In order to motivate the colleagues, the generator of the map above is loaded below.

C++ Generator of cures

/* Files ado.cin, conto.cin, Tania.cin, LambertW.cin, SuZex.cin should be loaded in order to compile the code below. */

 #include <math.h>
 #include <stdio.h>
 #include <stdlib.h>
 #define DB double
 #define DO(x,y) for(x=0;x<y;x++)
 using namespace std;
 #include<complex>
 typedef complex<double> z_type;
 #define Re(x) x.real()
 #define Im(x) x.imag()
 #define I z_type(0.,1.)
 #include "conto.cin"

 #include "tania.cin"
 #include "LambertW.cin"
 #include "SuZex.cin"
 //#include "AuZex.cin" 

 z_type tra(z_type z) {return z+exp(z);}

// z_type sutra(z_type z){ if( Re(z)<2. || fabs(Im(z))>2. ) return log(suzex(z));
 z_type sutra(z_type z){ if( Re(z)<2. ) return log(suzex(z));
                                        return tra(sutra(z-1.));}

 main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
 //DB x1=-1.1259817765745026; DO(n,8){ y=Re(suzex(x1)); x=y-1.; x1+=-1.2*x; printf("%18.16f %18.16f\n", x1,y);} getchar();
 int M=1001,M1=M+1;
 int N=1001,N1=N+1;
 DB X[M1],Y[N1];
 DB *g, *f, *w; // w is working array.
 g=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
 f=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
 w=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
 char v[M1*N1]; // v is working array
 FILE *o;o=fopen("SuTraMap.eps","w");  ado(o,2002,2002);
 fprintf(o,"1001 1001 translate\n 100 100 scale\n");
 fprintf(o,"1 setlinejoin 2 setlinecap\n");
 DO(m,M1) X[m]=-10+.02*(m-.5);
 DO(n,N1) Y[n]=-10+.02*(n-.5); 
 //for(n=0;n<N1;n++) { Y[n]=1.09*sinh((3./200.)*(n-200)); printf("%3d %9.6f\n",n,Y[n]); }
 for(m=-10;m<11;m++){M(m,-10) L(m,10)  }
 for(n=-10;n<11;n++){M(  -10,n) L(10,n)}
  fprintf(o,".006 W 0 0 0 RGB S\n");
 DO(m,M1)DO(n,N1){      g[m*N1+n]=999;
                        f[m*N1+n]=999;}
 DO(m,M1){x=X[m]; if(m/10*10==m) printf("x=%6.3f\n",x);
 DO(n,N1){y=Y[n]; z=z_type(x,y); //if(abs(z+2.)>.019)
 // c=AuZex01(z-1.);
 // c=AuZexAsy(LambertW(z))+1.;
 //c=log(suzex(z));
   c=sutra(z);
 // p=abs(c-z)/(abs(c)+abs(z)); p=-log(p)/log(10.); if(p>0 && p<17) g[m*N1+n]=p;
  p=Re(c); q=Im(c); if(p>-19 && p<19 && ( x<2. ||  fabs(q)>1.e-12 && fabs(p)>1.e-12) ){ g[m*N1+n]=p;f[m*N1+n]=q;}
        }}
 fprintf(o,"1 setlinejoin 1 setlinecap\n");
  p=1.2;q=.4;
 /*  p=9;q=.16;
  conto(o,g,w,v,X,Y,M,N,(15.3 ),-p,p); fprintf(o,".01 W .4 1 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N,(15.  ),-p,p); fprintf(o,".02 W 1 0 1 RGB S\n");
  conto(o,g,w,v,X,Y,M,N,(14.7 ),-p,p); fprintf(o,".01 W 1 .5 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N,(14.  ),-p,p); fprintf(o,".01 W .2 .2 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N,(13.  ),-p,p); fprintf(o,".01 W 0 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N,(12.  ),-p,p); fprintf(o,".03 W 0 0 1 RGB S\n");
  conto(o,g,w,v,X,Y,M,N,(11.  ),-p,p); fprintf(o,".01 W 0 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N,(10.  ),-p,p); fprintf(o,".01 W 0 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (9.  ),-p,p); fprintf(o,".03 W 0 1 1 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (8.  ),-p,p); fprintf(o,".01 W 0 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (7.  ),-p,p); fprintf(o,".01 W 0 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (6.  ),-p,p); fprintf(o,".04 W 0 .5 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (5.  ),-p,p); fprintf(o,".01 W 0 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (4.  ),-p,p); fprintf(o,".01 W 0 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (3.  ),-p,p); fprintf(o,".02 W 1 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (2.  ),-p,p); fprintf(o,".01 W 0 0 0 RGB S\n");
  conto(o,g,w,v,X,Y,M,N, (1.  ),-p,p); fprintf(o,".02 W .5 0 0 RGB S\n");
 */
 for(m=-8;m<8;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q,q);fprintf(o,".007 W 0 .6 0 RGB S\n");
 for(m=0;m<8;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q,q);fprintf(o,".007 W .9 0 0 RGB S\n");
 for(m=0;m<8;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q,q);fprintf(o,".007 W 0 0 .9 RGB S\n");
 for(m= 1;m<17;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p);fprintf(o,".02 W .8 0 0 RGB S\n");
 for(m= 1;m<17;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p);fprintf(o,".02 W 0 0 .8 RGB S\n");
                conto(o,f,w,v,X,Y,M,N, (0.  ),-2*p,2*p); fprintf(o,".02 W .5 0 .5 RGB S\n");
 for(m=-16;m<17;m++)conto(o,g,w,v,X,Y,M,N,(0.+m),-p,p);fprintf(o,".02 W 0 0 0 RGB S\n");
 // fprintf(o,"0 setlinejoin 0 setlinecap\n");
 // M(-10,0)L(0,0) fprintf(o,"1 1 1 RGB .02 W S\n");
 //#include "plofu.cin"
 fprintf(o,"showpage\n");
 fprintf(o,"%c%cTrailer\n",'%','%');
 fclose(o);  free(f); free(g); free(w);
       system("epstopdf SuTraMap.eps"); 
       system(    "open SuTraMap.pdf"); //for macintosh
       getchar(); system("killall Preview"); // For macintosh
 }

Latex generator of labels

%

\documentclass[12pt]{article} % <br>
\paperwidth 2004px %  <br>
\paperheight 2004px %  <br>
\textwidth 2394px %  <br>
\textheight 2300px %  <br>
\topmargin -101px %  <br>
\oddsidemargin -70px %  <br>
\usepackage{graphics} %  <br>
\usepackage{rotating} %  <br>
\newcommand \sx {\scalebox} %  <br>
\newcommand \rot {\begin{rotate}} %  <br>
\newcommand \ero {\end{rotate}} %  <br>
\newcommand \ing {\includegraphics} %  <br>
\newcommand \rmi {\mathrm{i}} %  <br>
\parindent 0pt
\pagestyle{empty}
\begin{document} %  <br>
\parindent 0pt %  <br>
\sx{1}{\begin{picture}(2002,2002) % <br>
%\put(40,20){\ing{b271tMap3}} %  <br>
%\put(40,20){\ing{ExpMap}} %  <br>
\put(30,1950){\sx{8}{$y$}} %  <br>
\put(30,1780){\sx{7}{$8$}} %  <br>
\put(30,1580){\sx{7}{$6$}} %  <br>
\put(30,1380){\sx{7}{$4$}} %  <br>
\put(30,1180){\sx{7}{$2$}} %  <br>
\put(30,0980){\sx{7}{$0$}} %  <br>
\put(-22,780){\sx{7}{$-2$}} %  <br>
\put(-22,580){\sx{7}{$-4$}} %  <br>
\put(-22,380){\sx{7}{$-6$}} %  <br>
\put(-22,180){\sx{7}{$-8$}} %  <br>
\put(120, 6){\sx{7}{$-8$}} %  <br>
\put(320, 6){\sx{7}{$-6$}} %  <br>
\put(520, 6){\sx{7}{$-4$}} %  <br>
\put(720, 6){\sx{7}{$-2$}} %  <br>
\put(988, 6){\sx{7}{$0$}} %  <br>
\put(1188, 6){\sx{7}{$2$}} %  <br>
\put(1388, 6){\sx{7}{$4$}} %  <br>
\put(1588, 6){\sx{7}{$6$}} %  <br>
\put(1788, 6){\sx{7}{$8$}} %  <br>
\put(1958, 6){\sx{8}{$x$}} %  <br>
\put(0,0){\ing{SuTraMap}} %  <br>
%\zoomax %  <br>

\put(200,1414){\sx{7}{\rot{56}$u\!=\!-2.2$\ero}} %  <br>
\put(352,1328){\sx{7}{\rot{56}$u\!=\!-2$\ero}} %  <br>
\put(462,1238){\sx{7}{\rot{56}$u\!=\!-1.8$\ero}} %  <br>
\put(574,1188){\sx{7}{\rot{56}$u\!=\!-1.6$\ero}} %  <br>
\put(652,1130){\sx{7}{\rot{56}$u\!=\!-1.4$\ero}} %  <br>
\put(722,1070){\sx{7}{\rot{58}$u\!=\!-1.2$\ero}} %  <br>
\put(790,1050){\sx{7}{\rot{59}$u\!=\!-1$\ero}} %  <br>

\put(1518,1200){\sx{7}{\rot{10}$v\!=\!3$\ero}} %  <br>
\put(1277,1590){\sx{7}{\rot{68}$v\!=\!2$\ero}} %  <br>
\put(618,1632){\sx{7}{\rot{-53}$v\!=\!1$\ero}} %  <br>
\put(340,1128){\sx{7}{\rot{-10}$v\!=\!0.2$\ero}} %  <br>
\put(310,0984){\sx{7}{$v\!=\!0$}} %  <br>
\put(330,0832){\sx{7}{\rot{10}$v\!=\!-0.2$\ero}} %  <br>
\put(642,0332){\sx{7}{\rot{53}$v\!=\!-1$\ero}} %  <br>
\put(1209,488){\sx{7}{\rot{-70}$v\!=\!-2$\ero}} %  <br>
\put(1490,772){\sx{7}{\rot{-11}$v\!=\!-3$\ero}} %  <br>
\end{picture}} %  <br>
\end{document} %  <br>
%

References

↑ https://mizugadro.mydns.jp/BOOK/468.pdf D.Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.
↑ https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
https://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014
↑ ^3.0 ^3.1 https://www.m-hikari.com/ams/ams-2013/ams-129-132-2013/kouznetsovAMS129-132-2013.pdf
https://mizugadro.mydns.jp/PAPERS/2013hikari.pdf D.Kouznetsov. Entire Function with Logarithmic Asymptotic. Applied Mathematical Sciences, Vol. 7, 2013, no. 131, 6527 - 6541

Keywords

«Entire function with logarithmic asymptotic», «Complex map», «Latex», «Superfunction», «Superfunctions», «SuTra», «SuZex», «Zex»,

«Суперфункции»,

File history

Click on a date/time to view the file as it appeared at that time.

	Date/Time	Thumbnail	Dimensions	User	Comment
current	17:50, 20 June 2013		4,176 × 4,176 (1.76 MB)	Maintenance script (talk \| contribs)	Importing image file

You cannot overwrite this file.

File usage

The following 2 pages use this file:

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Horizontal resolution	150 dpi
Vertical resolution	150 dpi

[1] ttps://mizugadro.mydns.jp/BOOK/468.pdf D.Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.

[2] ttps://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
https://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014

[hikari-3] 3.0 ^3.1 https://www.m-hikari.com/ams/ams-2013/ams-129-132-2013/kouznetsovAMS129-132-2013.pdf
https://mizugadro.mydns.jp/PAPERS/2013hikari.pdf D.Kouznetsov. Entire Function with Logarithmic Asymptotic. Applied Mathematical Sciences, Vol. 7, 2013, no. 131, 6527 - 6541

[1]

[2]

[3]