Difference between revisions of "Discrete Fourier"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
| − | For natural number |
+ | For natural number \(N>1\), the '''Discrete Fourier''' is operator \(\hat ふ_N\) |
| − | acting on |
+ | acting on \(N\)-vector \(A\) in such a way that |
| − | : |
+ | : \(\!\!\!\!\!\!\!\!\!\!\! (1) ~ ~ ~ \displaystyle (\hat ふ_{N} A)_n = \sum_{m=0}^{N-1} ふ_{n,m} A_m\) |
| − | While deal with Fourier operators, it is convenient to begin numeration with zero. Elements of matrix |
+ | While deal with Fourier operators, it is convenient to begin numeration with zero. Elements of matrix \(ふ\) are |
| − | : |
+ | : \(\!\!\!\!\!\!\!\!\!\!\! (2) ~ ~ ~ \displaystyle ふ_{m,n}=\frac{1}{\sqrt{N}} \exp\! \left( \frac{- \mathrm i ~2 ~\pi}{N}~m~n\right)\) |
| − | The Fourier matrix |
+ | The Fourier matrix \(ふ\) is symmetric and unitary; |
| − | : |
+ | : \(\!\!\!\!\!\!\!\!\!\!\! (3) ~ ~ ~ \displaystyle ふ_{m,n}= ふ_{n,m}\) |
| − | : |
+ | : \(\!\!\!\!\!\!\!\!\!\!\! (4) ~ ~ ~ \displaystyle {\hat ふ}^*= {\hat ふ}^{-1}\) |
| − | in such a way, if |
+ | in such a way, if \(A=\hat ふ B\), then \(B={\hat ふ}^* A\); so, \({\hat ふ}^\dagger={\hat ふ}^*\). |
==Different notations== |
==Different notations== |
||
| − | Sometimes, the operator that deviate from |
+ | Sometimes, the operator that deviate from \(\hat ふ\) with factor \(\sqrt{N}\) is considered; for such modified operator, the equation (4) does not hold, but the mofified operator is still called "Discrete Fourier" |
<ref> |
<ref> |
||
http://en.wikipedia.org/wiki/Discrete_Fourier_transform |
http://en.wikipedia.org/wiki/Discrete_Fourier_transform |
||
| − | </ref>. Often, such an operator is denoted with latin letter |
+ | </ref>. Often, such an operator is denoted with latin letter \(F\). (Sometimes the special font is used to avoid the confusion with parameters and functions.) |
In order to avoid confusions, in TORI, the [[hiragana]] <ref>http://en.wikipedia.org/wiki/Hiragana</ref> character |
In order to avoid confusions, in TORI, the [[hiragana]] <ref>http://en.wikipedia.org/wiki/Hiragana</ref> character |
||
| − | ふ is used for the (normalized) Fourier operator, so, here, |
+ | ふ is used for the (normalized) Fourier operator, so, here, \(ふ_N\) character denotes "DiscreteFourier with \(N\) points" and nothing else. |
==Numeric implementation of the discrete Fourier== |
==Numeric implementation of the discrete Fourier== |
||
| − | The numeric implementation of the Discrete Fourier is especially efficient when |
+ | The numeric implementation of the Discrete Fourier is especially efficient when \(N=2^k\) for some natural number \(k\). |
For this case, the example of implementation is suggested below: |
For this case, the example of implementation is suggested below: |
||
| Line 59: | Line 59: | ||
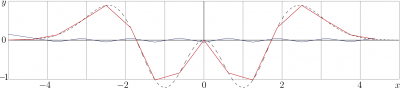
[[File:FourierExampleGauss16pol04Ta.png|400px|thumb|Numerical approximation of the Fourier transform of function |
[[File:FourierExampleGauss16pol04Ta.png|400px|thumb|Numerical approximation of the Fourier transform of function |
||
| − | + | \(~f(x)=\exp(−x^2/2)x^2(−3\!+\!x^2)~\) with \(N\!=\!16\)]] |
|
| − | For the continuous square-integrable functions, the discrete approximation with |
+ | For the continuous square-integrable functions, the discrete approximation with \(N\) points can be written with uniform mesh at pointd \(x_n\), \(n=0..N\), such that |
| − | : |
+ | : \(\displaystyle x_N=(n-N/2) \sqrt{\frac {2\pi}{N}}\) |
| − | Let |
+ | Let \(f_n=f(x_n)\) |
| − | then at the points |
+ | then at the points \(x_n\), the Fourier-transform \(g=\mathcal F f\) |
can be approximated with the sum: |
can be approximated with the sum: |
||
| − | : |
+ | : \( \displaystyle g(x_n)= \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \exp(\mathrm i x_n y) f(y) \mathrm d y |
\approx g_n= |
\approx g_n= |
||
\frac{1}{\sqrt{N}} |
\frac{1}{\sqrt{N}} |
||
\sum_{n=0}^{N-1} \exp(\mathrm i x_n x_m) f_m |
\sum_{n=0}^{N-1} \exp(\mathrm i x_n x_m) f_m |
||
| + | \) |
||
| − | $ |
||
| − | Then, at large |
+ | Then, at large \(N\gg 1\), the array \(g_n\) approximates \(g(x_n)\). Using the routine fft for the discrete Fourier above, |
the numerical implementation of Fourier operator with the formula above may have the following form: |
the numerical implementation of Fourier operator with the formula above may have the following form: |
||
| Line 81: | Line 81: | ||
for(j=0;j<N/2;j++) {c=b[j];b[j]=b[j+N/2]*q;b[j+N/2]=c*q;} |
for(j=0;j<N/2;j++) {c=b[j];b[j]=b[j+N/2]*q;b[j+N/2]=c*q;} |
||
} |
} |
||
| − | where |
+ | where \(b\) is array to store the function and its Fourier, |
| − | + | \(N\) is number of points, and \(o=1\) for the direct Fouried and \(o=-1\) for the conjugated (inverse) Fourier. |
|
As an example, the figure at right shows discrete approximation of the self-Fourier function |
As an example, the figure at right shows discrete approximation of the self-Fourier function |
||
| − | + | \(~f(x)=\exp(−x^2/2)x^2(−3\!+\!x^2)~\) at the mesh with \(N\!=\!16\). |
|
| − | Values |
+ | Values \(f(x_n)\) and \(g(x_n)\) almost coincide; they are shown with the segmented line. |
| − | The difference scaled with factor |
+ | The difference scaled with factor \(100\) is shown with the saw-like line that oscillates in vicinity of zero. |
==Approximation of the Fourier-series== |
==Approximation of the Fourier-series== |
||
| − | Consider, for continuous function |
+ | Consider, for continuous function \(f\) and given \(N\), array |
| − | + | \(F_n=f\left(\frac{2 \pi}{N} n\right)\) |
|
| − | Then, at large |
+ | Then, at large \(N\) the interpolation of array \(F\) can be considered as approximation of function \(f\), and its Discrete Fourier gives an approximation of the Fourier coefficients |
| − | : |
+ | : \(\!\!\!\!\!\!\!\!\!\! \displaystyle g_n=\frac{1}{2 \pi} \int_0^{2\pi} \exp\left( \mathrm i n x\right) f(x) \mathrm d x |
\approx |
\approx |
||
\displaystyle \frac{1}{2 \pi} |
\displaystyle \frac{1}{2 \pi} |
||
| Line 103: | Line 103: | ||
= |
= |
||
\frac{1}{\sqrt{N}} (\hat ふ_N F)_n |
\frac{1}{\sqrt{N}} (\hat ふ_N F)_n |
||
| + | \) |
||
| − | $ |
||
in the Fourier series |
in the Fourier series |
||
| − | : |
+ | : \( \!\!\!\!\!\!\!\!\!\!\displaystyle |
| − | f(x)= \sum_{n=0}^{\infty} ~ g_n \exp( i n x) |
+ | f(x)= \sum_{n=0}^{\infty} ~ g_n \exp( i n x) \) |
In such a way, the discrete Fourier operator can be used for approximation of both, the [[Fourier transform]] and the coefficients of the [[Fourier series]]. |
In such a way, the discrete Fourier operator can be used for approximation of both, the [[Fourier transform]] and the coefficients of the [[Fourier series]]. |
||
Latest revision as of 18:48, 30 July 2019
For natural number \(N>1\), the Discrete Fourier is operator \(\hat ふ_N\) acting on \(N\)-vector \(A\) in such a way that
- \(\!\!\!\!\!\!\!\!\!\!\! (1) ~ ~ ~ \displaystyle (\hat ふ_{N} A)_n = \sum_{m=0}^{N-1} ふ_{n,m} A_m\)
While deal with Fourier operators, it is convenient to begin numeration with zero. Elements of matrix \(ふ\) are
- \(\!\!\!\!\!\!\!\!\!\!\! (2) ~ ~ ~ \displaystyle ふ_{m,n}=\frac{1}{\sqrt{N}} \exp\! \left( \frac{- \mathrm i ~2 ~\pi}{N}~m~n\right)\)
The Fourier matrix \(ふ\) is symmetric and unitary;
- \(\!\!\!\!\!\!\!\!\!\!\! (3) ~ ~ ~ \displaystyle ふ_{m,n}= ふ_{n,m}\)
- \(\!\!\!\!\!\!\!\!\!\!\! (4) ~ ~ ~ \displaystyle {\hat ふ}^*= {\hat ふ}^{-1}\)
in such a way, if \(A=\hat ふ B\), then \(B={\hat ふ}^* A\); so, \({\hat ふ}^\dagger={\hat ふ}^*\).
Different notations
Sometimes, the operator that deviate from \(\hat ふ\) with factor \(\sqrt{N}\) is considered; for such modified operator, the equation (4) does not hold, but the mofified operator is still called "Discrete Fourier" [1]. Often, such an operator is denoted with latin letter \(F\). (Sometimes the special font is used to avoid the confusion with parameters and functions.)
In order to avoid confusions, in TORI, the hiragana [2] character ふ is used for the (normalized) Fourier operator, so, here, \(ふ_N\) character denotes "DiscreteFourier with \(N\) points" and nothing else.
Numeric implementation of the discrete Fourier
The numeric implementation of the Discrete Fourier is especially efficient when \(N=2^k\) for some natural number \(k\). For this case, the example of implementation is suggested below:
/* //Example of headers #include<math.h> #include<stdio.h> #include <stdlib.h> #include <complex> using namespace std; #define z_type complex<double> */ // The "miminal" Fast Fourier Transform by Dmitrii Kouznetsov // n should be 2^m for entire m ; o should be 1 or -1 ;
void fft(z_type *a, int N, int o) // Arry is FIRST!
{z_type u,w,t; int i,j,k,l,e=1,L,p,q,m;
q=N/2; p=2; for(m=1;p<N;m++) p*=2;
p=N-1; z_type y=z_type(0.,M_PI*o); j=0;
for(i=0;i<p;i++){ if(i<j) { t=a[j]; a[j]=a[i]; a[i]=t;}
k=q; while(k<=j){ j-=k; k/=2;}
j+=k; }
for(l=0;l<m;l++)
{ L=e; e*=2; u=1.; w=exp(y/((double)L));
for(j=0;j<L;j++)
{ for(i=j;i<N;i+=e){k=i+L; t=a[k]*u; a[k]=a[i]-t; a[i]+=t;}
u*=w;
} }
}
Approximation of the Fourier operator
For the continuous square-integrable functions, the discrete approximation with \(N\) points can be written with uniform mesh at pointd \(x_n\), \(n=0..N\), such that
- \(\displaystyle x_N=(n-N/2) \sqrt{\frac {2\pi}{N}}\)
Let \(f_n=f(x_n)\) then at the points \(x_n\), the Fourier-transform \(g=\mathcal F f\) can be approximated with the sum:
- \( \displaystyle g(x_n)= \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \exp(\mathrm i x_n y) f(y) \mathrm d y \approx g_n= \frac{1}{\sqrt{N}} \sum_{n=0}^{N-1} \exp(\mathrm i x_n x_m) f_m \)
Then, at large \(N\gg 1\), the array \(g_n\) approximates \(g(x_n)\). Using the routine fft for the discrete Fourier above, the numerical implementation of Fourier operator with the formula above may have the following form:
void fafo(z_type *b,int N,int o)
{ int j; z_type c; double q=sqrt(1./N);
for(j=0;j<N/2;j++) {c=b[j];b[j]=b[j+N/2];b[j+N/2]=c;}
fft(b,N,o);
for(j=0;j<N/2;j++) {c=b[j];b[j]=b[j+N/2]*q;b[j+N/2]=c*q;}
}
where \(b\) is array to store the function and its Fourier, \(N\) is number of points, and \(o=1\) for the direct Fouried and \(o=-1\) for the conjugated (inverse) Fourier.
As an example, the figure at right shows discrete approximation of the self-Fourier function \(~f(x)=\exp(−x^2/2)x^2(−3\!+\!x^2)~\) at the mesh with \(N\!=\!16\). Values \(f(x_n)\) and \(g(x_n)\) almost coincide; they are shown with the segmented line. The difference scaled with factor \(100\) is shown with the saw-like line that oscillates in vicinity of zero.
Approximation of the Fourier-series
Consider, for continuous function \(f\) and given \(N\), array
\(F_n=f\left(\frac{2 \pi}{N} n\right)\)
Then, at large \(N\) the interpolation of array \(F\) can be considered as approximation of function \(f\), and its Discrete Fourier gives an approximation of the Fourier coefficients
- \(\!\!\!\!\!\!\!\!\!\! \displaystyle g_n=\frac{1}{2 \pi} \int_0^{2\pi} \exp\left( \mathrm i n x\right) f(x) \mathrm d x \approx \displaystyle \frac{1}{2 \pi} \sum_{m=0}^{N-1} \exp\left(- \mathrm i n \frac{2 \pi}{N} m \right) \frac{2 \pi}{N}= \frac{1}{N} \sum_{m=0}^{N-1} \exp\left(\frac{2 \pi \mathrm i}{N} mn \right) = \frac{1}{\sqrt{N}} (\hat ふ_N F)_n \)
in the Fourier series
- \( \!\!\!\!\!\!\!\!\!\!\displaystyle f(x)= \sum_{n=0}^{\infty} ~ g_n \exp( i n x) \)
In such a way, the discrete Fourier operator can be used for approximation of both, the Fourier transform and the coefficients of the Fourier series. Similar approach can be used for other integral transforms; in particular, for the CosFourier and the SinFourier operators.
Application of the Discrete Fourier
The discrete implementation of the Fourier transform is useful for the numerical analysis of solutions of linear equations and, in particular, those of the paraxial approximation in wave optics. [3][4][5].
References
- ↑ http://en.wikipedia.org/wiki/Discrete_Fourier_transform
- ↑ http://en.wikipedia.org/wiki/Hiragana
- ↑ http://mizugadro.mydns.jp/PAPERS/josa1f0.pdf D.Kouznetsov, J.V.Moloney, E.M.Wright. Efficiency of pump in the double-clad fiber amplifiers. 1. Fiber with circular symmetry. -- J.O.S.A. B, June 2001, V.18, No.6, p.743-749.
- ↑ http://mizugadro.mydns.jp/PAPERS/josa2f0.pdf D.Kouznetsov, J.V.Moloney. Efficiency of pump in the double-clad fiber amplifiers. 2. Broken circular symmetry. -- J.O.S.A. B, V.19, No.6, p.1259-1263 (2002).
- ↑ http://mizugadro.mydns.jp/PAPERS/josa3f0.pdf D.Kouznetsov, J.V.Moloney. Efficiency of pump absorption in double-clad fibers amplifiers. 3. Calculation of modes -- J.O.S.A. B, V.19, No.6, p.1304-1309 (2002).