Maga

$y\!=\!\mathrm{maga}(x)$ (thick black curve) and related functions

Function maga appears at the consideration of the principal mode guided by the set of pinholes, and expresses the loss of the guiding.

The scalar product of function mori to itself with quadratic defacement is denoted with identifier naga

$\mathrm{naga}(x)=\displaystyle 2 \int_0^\infty \mathrm{mori}(p )^2 \exp(\mathrm i p^2 x) \, p \,\mathrm d p$

Function mori is defined with

mori$(p)=\displaystyle \frac{J_0(L p)}{1-p^2}$

and the corresponding limit at $p\!=\!\pm 1$;

$L\!\approx\!2.404825557695773$ is the first zero of the Bessel function of 0th order, $J_0(L)\!=\!0$.

The normalisation factor $2$ in the definition is chosen in such a way that $\mathrm{naga}(0)\!=\!1$.

Then, for real values of the argument, maga is defined with

$\mathrm{maga}(x)=1-|\mathrm{naga}(x)|^2$

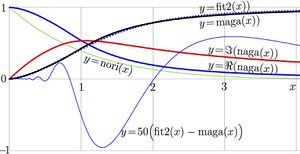
The explicit plot of function maga is shown with black curve in the figure at top.

Properties

$\mathrm{maga}(-x)= \mathrm{maga}(x)^*$

although the range of holomorphism gof this function is not yet well analysed, it is obvious that this function is singular at zero. For small real values of its argument,

$\mathrm {maga}(x)= C_0\, x^{3/2} \big(1+c_1 x+O(x)^{3/2}\big)$

where $C_0$ and $c_1$ are constants;

$C_0\approx 0.44238$

$c_1\approx - 0.085$

Precise evaluation of constant $C_0$ requires either integration of oscillating function (that is slow, if performed in a straightforward way), or search for the appropriate contour integral in the complex plane. For the last option, the holomorphic properties of the functions involved (and their complex maps) should be analysed.

At large real values of the argument, maga approaches unity; $~\displaystyle \lim_{x\rightarrow 0} \,\mathrm{maga}(x)=1$.

Fourier

Integral in the definition of functionMaga can be expressed through the Fourier transforms of function nori defined with

nori$(x)=\,$kori$^2(x)=\,$mori$\big(\sqrt{x}\big)^2$.

Function nori is shown in figure at the top with thin green line. Then, the change of variable of integration definition of function naga becomes straightforward. Let $q=p^2$; then, $\mathrm dq=2 p\mathrm dp$, and

$\displaystyle \mathrm{naga}(x)=\int_0^\infty \mathrm{nori}(q) \, \exp(\mathrm i \,q\, x)\, \mathrm d q=\mathrm{nagc}(x) + \mathrm i ~\mathrm{nags}(x)$

where

nagc$(x)=\displaystyle \int_0^\infty \mathrm{nori}(q) \, \cos(q\, x)\, \mathrm d q$

nags$(x)=\displaystyle \int_0^\infty \mathrm{nori}(q) \, \sin(q\, x)\, \mathrm d q$

appear as non-normalised CosFT and SinFT of function nori for real argument $x$. These two functions are shown with thick blue and thick red lines in the figures at top.

Then, function maga appears in the following way:

$\mathrm {maga}(z)=1-\mathrm{nagc}(z)^2-\mathrm{nags}(z)^2$

This representation indicates the way of holomorphic extension of function maga for complex values of the argument $z$; the appropriate paths of integration should be chosen in the integrals for nagc$(z)$ and nags$(z)$ in order to provide the convergence.

As the straightforward evaluation of function maga through the SinFT and CosFT is not efficient, several service functions are suggested to boost the evaluation.

Small argument

For application to the pinhole waveguide, case of small argument is especially important. In order to boost evaluation in this case, define

nag$(x)=\int_0^{\infty} \mathrm{kori}(x)^2 (1-\cos(q\,x)) \,\mathrm d q$

Due to the unity norm of function kori, the following relation takes place: nag$(x)=1-\,$nagc$(x)$, and

nagc$(x)=1-\,$nag$(x)$

Then,

mori$(x)=1-\big(1-\mathrm{nag}(x)\big)^2-\mathrm{nags}(x)^2=2\,\mathrm{nag}(x)-\mathrm{nag}(x)^2-\mathrm{nags}(x)^2$

The first term in the last expression determines the leading term in the asymptotic expansion of function mori at the small values of its argument.

Fitting

The representation above can be used for evaluation and for the figging of function maga.

One of the simple fiting is provided with formula

$\mathrm{fit2}(x)=\displaystyle \frac{x^{3/2}}{\sqrt{5-x/2+x^2/4+x^3}}$

This fit is shown in the figure at top with dotted line. It is close to the straight curve $y=\mathrm{maga}(x)$. In order to see deviation of function fit2 from function maga, the difference, scaled with factor 50, is shown in the bottom part of the graphic. The difference oscillates, these oscillations become rapid and small at small values of the argument.

Finction fit2 provides at least 2 significant figures of function maga and can be useful in the design of the pinhole waveguides.

Application

Function maga describes the first approximation loss in the pinhole waveguide, in the limit of small loss. The argument $p$ of maga$(p )$ has the following meaning:

$\displaystyle p= \frac{T}{2 k} \left(\frac{L_1}{r}\right)^2$

where $k$ is wavenumber, $r$ is radius of the pinholes, and $T$ is distance between the pinholes. Then, function maga gives the first approximation in the loss of the Bessel mode in such a waveguide, in the limit of small $p$.

The straightforward numerical integration in the definition of maga is not efficient, even for real $p$; for this reason, the analytical properties of the integrand, and, in particular, those of function kori, deserve the detailed investigation, analysis and description.

The goal is to calculate the asymptotic expansion of function maga at small values of its argument, ($\,|p| \!\ll\! 1\,$), at large values of its argument ($\,|p|\!\gg\! 1\,$), to check agreement between the approximations, based on these expansions, and to generate the complex map of function maga. For this goal, the fast and precise implementation of function kori is necessary.

It may have sense to consider first the function naga defined as

naga$(p )=\displaystyle \int_0^\infty \mathrm{kori}(x)^2\, \exp(\mathrm i p x) \, \mathrm d x$

then $~$ maga$(z)=1-\mathrm{naga}(z)\, \mathrm{naga}(z^*)^*$

Several articles about the functions introduced above are expected to be loaded in TORI. (Some of them ar already loaded, in particular, mori, nori and kori, but they are still far from the ideal description of a special function) Then it will be possible to choose the most efficient representation and description of function maga, using some of these functions.

The names kori, nori, mori, maga and naga, suggested for the functions involved, are tentative; they may be reconsidered and redefined for the analysis of the expansion of the mode of the pinhole waveguide with respect to the Bessel modes and more accurate estimate of the loss in such a waveguide.

In such a way, the descriptions and implementations of these functions appear as tools for the description of the pinhole waveguide, following the general ideology of TORI. Construction of these functions may look as a routine, dirty job (неблагодарная, не видная работа), that will not be appreciated by the scientific community, but, still, somebody is supposed to do it. Then, after a time, these functions may have also other applications. In particular, they may be useful for the "ab initio" calculus of the quantum reflection of excited atoms from a wall). Keeping in mind these applications, in have sense to perform the detailed analysis; to get the asymptotic expansions and the implementations with many decimal digits.

Keywords

Bessel transform, CosFT FFT, Morinaga function, Naga, Nori, SinFT,