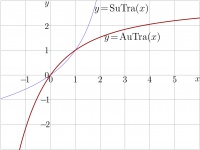
AuTra
AuTra or ArcTra or ArcTrappmann function is the inverse function of SuTra.
AuTra is Abel function of the Trappmann function, $\mathrm{tra}(z)=z+\exp(z)$.
AuTra satisfies the Abel equation
$ \mathrm{AuTra} \Big( \mathrm{tra}(z) \Big)= \mathrm{AuTra}(z)+1$
and the additional condition
$ \mathrm{AuTra}(1)=0$
This condition corresponds to relation $\mathrm{SuTra}(0)=1$. The same choice of the initial value is used also for many other superfunctions, including tetration, SuZex function, Tania function and Shoka function.
AuTra is real-holomorphic, $\mathrm{AuTra}(z^*)=\mathrm{AuTra}(z)^*$
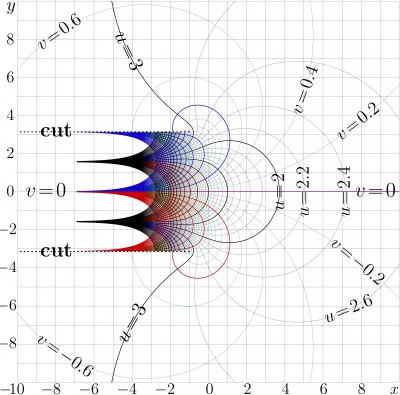
Branch points and the cut lines
AuTra has two branch points $~-1\!+\!\mathrm i~$ and $~-1\!-\!\mathrm i~$; the cut lines are directed to the left hand side of the complex plane, parallel to the real axis. In TORI, this is default choice of the cut lines.