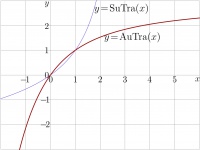
AuTra

$u\!+\!\mathrm i v= \mathrm{AuTra}(x\!+\!\mathrm i y)$

$y= \mathrm{AuTra}(x)$

AuTra or ArcTra or ArcTrappmann function is the inverse function of SuTra.

AuTra is Abel function of the Trappmann function, $\mathrm{tra}(z)=z+\exp(z)$.

AuTra satisfies the Abel equation

$ \mathrm{AuTra} \Big( \mathrm{tra}(z) \Big)= \mathrm{AuTra}(z)+1$

and the additional condition

$ \mathrm{AuTra}(1)=0$

This condition corresponds to relation $\mathrm{SuTra}(0)=1$. The same choice of the initial value is used also for many other superfunctions, including tetration, SuZex function, Tania function and Shoka function.

AuTra is real-holomorphic, $\mathrm{AuTra}(z^*)=\mathrm{AuTra}(z)^*$

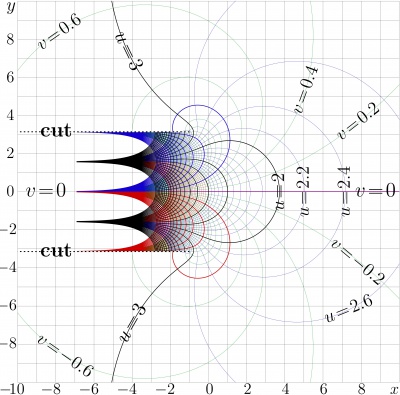
Branch points and the cut lines

AuTra has two branch points $~-1\!+\!\mathrm i~$ and $~-1\!-\!\mathrm i~$; the cut lines are directed to the left hand side of the complex plane, parallel to the real axis. In TORI, this is default choice of the cut lines.

Keywords

Abel function, Trappmann function