Difference between revisions of "AuZex"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
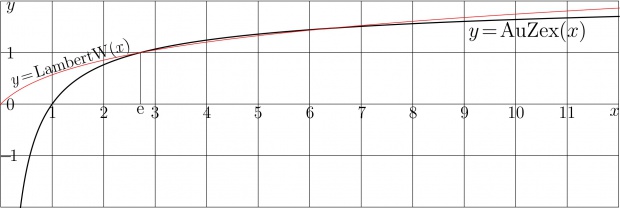
[[File:AuZexLamPlotT.jpg|620px|thumb|Fig.1. Plot of [[AuZex]] (thick curve) in comparison to [[LambertW]] (thin curve) ]] |
[[File:AuZexLamPlotT.jpg|620px|thumb|Fig.1. Plot of [[AuZex]] (thick curve) in comparison to [[LambertW]] (thin curve) ]] |
||
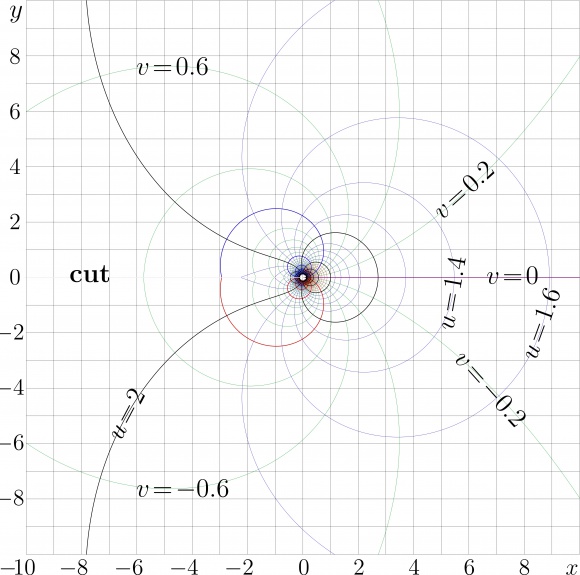
| − | [[File:AuZexMapT.jpg|580px|thumb|Fig.2. [[Complex map]], |
+ | [[File:AuZexMapT.jpg|580px|thumb|Fig.2. [[Complex map]], \(u\!+\!\mathrm i = \mathrm {AuZex}(x\!+\!\mathrm i y)\)]] |
| − | [[Auzex]] is inverse function of [[SuZex]]; |
+ | [[Auzex]] is inverse function of [[SuZex]]; \(\mathrm{AuZex} = \mathrm{SuZex}^{-1}\) |
| − | [[AuZex]] is also [[Abel function]] for the [[transfer function]] |
+ | [[AuZex]] is also [[Abel function]] for the [[transfer function]] \(\mathrm{zex}(z)=z \exp(z)\). |
==Basic properties== |
==Basic properties== |
||
| − | [[AuZex]] is [[Inverse function]] of [[SuZex]], so, in wide ranges of values of |
+ | [[AuZex]] is [[Inverse function]] of [[SuZex]], so, in wide ranges of values of \(z\), the relations |
| − | (1) |
+ | (1) \( ~ ~ ~ {\rm SuZex}\Big( \mathrm{AuZex}(z) \Big) = z \) |
and |
and |
||
| − | (2) |
+ | (2) \( ~ ~ ~ \mathrm{AuZex}\Big( \mathrm{SuZex}(z) \Big) = z \) |
| − | hold. In particular, |
+ | hold. In particular, \(~\mathrm{AuZex}(1)=0\). |
Also, [[AuZex]] satisfies the [[Abel equation]] |
Also, [[AuZex]] satisfies the [[Abel equation]] |
||
| − | (3) |
+ | (3) \( ~ ~ ~ \mathrm{AuZex}\Big( \mathrm{zex}(z) \Big) = \mathrm{AuZex}(z) +1\) |
in this case, [[zex]] appears as [[transfer function]], and [[AuZex]] is its [[Abel function]]. |
in this case, [[zex]] appears as [[transfer function]], and [[AuZex]] is its [[Abel function]]. |
||
Iterations of equation (3) gives the relations |
Iterations of equation (3) gives the relations |
||
| − | (4) |
+ | (4) \( ~ ~ ~ \mathrm{AuZex}\Big( \mathrm{zex}^n(z) \Big) = \mathrm{AuZex}(z) +n\) |
This can be re-writtern also as |
This can be re-writtern also as |
||
| − | (5) |
+ | (5) \( ~ ~ ~ \mathrm{AuZex}\Big( \mathrm{LambertW}^n(z) \Big) = \mathrm{AuZex}(z) - n\) |
as [[LambertW]] is [[inverse function]] of [[zex]]. |
as [[LambertW]] is [[inverse function]] of [[zex]]. |
||
| Line 44: | Line 44: | ||
The name should be easy to remember, in order to have no need to copypast it from the description page each time of the use. |
The name should be easy to remember, in order to have no need to copypast it from the description page each time of the use. |
||
| − | The First letter "A" may refer to [[ArcSuZex]] or to [[Abel function]], as [[AuZex]] is [[inverse function]] of [[SuZex]] and [[Abel function]] of [[zex]], |
+ | The First letter "A" may refer to [[ArcSuZex]] or to [[Abel function]], as [[AuZex]] is [[inverse function]] of [[SuZex]] and [[Abel function]] of [[zex]], \(\mathrm{zex}(z)=z\exp(z)\). |
| − | The second letter "u" may indicate that upper side of the coordinate plane is used for the plot of the [[SuZex]]. For real values of the argument |
+ | The second letter "u" may indicate that upper side of the coordinate plane is used for the plot of the [[SuZex]]. For real values of the argument \(x\), [[Suzex]]\((x)\!>\!0\). |
The letter "d" may be used to create names [[SdZex]] and its inverse function [[AdZex]] for the other [[superfunction]] and [[Abel function]] of [[zex]], of as soon as these functions will be requested, implemented and loaded to [[TORI]]. |
The letter "d" may be used to create names [[SdZex]] and its inverse function [[AdZex]] for the other [[superfunction]] and [[Abel function]] of [[zex]], of as soon as these functions will be requested, implemented and loaded to [[TORI]]. |
||
| Line 54: | Line 54: | ||
==Fixed point of [[Zex]]== |
==Fixed point of [[Zex]]== |
||
| − | [[AuZex]] is [[Abel function]] for the [[transfer function]] |
+ | [[AuZex]] is [[Abel function]] for the [[transfer function]] \(T\!=\,\)[[zex]], which has the only one real [[fixed point]] \(L\!=\!0\). Aiming applications to the physics and, in particular, to the [[Laser science]], the real [[superfunction]]s and [[Abel function]]s are of special interest. This refers not namely [[zex]] as a transfer function for some strange [[amplifier]], but the method of constructing of real [[superfunction]]s and [[Abel function]]s; the real functions are more likely to be used in physical applications than those that have complex values along the real axis. For this reason, namely this fixed point is chosen as asymptotic value of [[SuZex]] at minus infinity. Correspondently, its inverse function |
[[AuZex]] has singularity at zero. |
[[AuZex]] has singularity at zero. |
||
The fixed point of the transfer function can be used for the expansion of the [[Abel function]]. For the transfer function [[zex]], the expansion of the Abel function begins with minus first power and logarithmic terms: |
The fixed point of the transfer function can be used for the expansion of the [[Abel function]]. For the transfer function [[zex]], the expansion of the Abel function begins with minus first power and logarithmic terms: |
||
| − | (6) |
+ | (6) \(~ ~ ~ \displaystyle \mathrm{AuZex}(z) \approx \frac{-1}{z}+\frac{1}{2}\ln(z)+\sum_{n=0}^N ~ c_n z^n\) |
The series does not seem to converge; the more terms are taken into account, the narrower is the range of the approximation. |
The series does not seem to converge; the more terms are taken into account, the narrower is the range of the approximation. |
||
| − | <!-- at least, it does not converge to |
+ | <!-- at least, it does not converge to \(\mathrm{AuZex(z)\) !--> |
| − | However, for small |
+ | However, for small \(|z|\), this expansion can be used for the fast and precise evaluation. |
| − | Similar situation takes place with expansion of [[ArcTetration]] at the fixed points |
+ | Similar situation takes place with expansion of [[ArcTetration]] at the fixed points \(L\) and \(L^*\) of the [[exponential]]; at the increase of precision or at the attempts to extend the range of the approximation, some additional terms |
(not specified in (6)) become significant. |
(not specified in (6)) become significant. |
||
| − | The expansion at [[fixed point]] zero provides of orderor of 15 decimal digits for |
+ | The expansion at [[fixed point]] zero provides of orderor of 15 decimal digits for \(N=12\) at \(|z|<0.1\) |
==Example of the "regular iteration"== |
==Example of the "regular iteration"== |
||
| − | Similar approach is used to implement two [[Abel function]]s of the exponential to to base |
+ | Similar approach is used to implement two [[Abel function]]s of the exponential to to base \(b=\exp^2(-1)=\exp(1/\mathrm e)\approx 1.444667861\) |
<ref> |
<ref> |
||
http://tori.ils.uec.ac.jp/PAPERS/2012e1eMcom2590.pdf |
http://tori.ils.uec.ac.jp/PAPERS/2012e1eMcom2590.pdf |
||
H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). [[Mathematics of Computation]], 2012 February 8. ISSN 1088-6842(e) ISSN 0025-5718(p) |
H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). [[Mathematics of Computation]], 2012 February 8. ISSN 1088-6842(e) ISSN 0025-5718(p) |
||
<!-- http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf Journal version (the registration may be required) !--> |
<!-- http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf Journal version (the registration may be required) !--> |
||
| − | </ref>. In that case, the [[transfer function]] |
+ | </ref>. In that case, the [[transfer function]] \(\exp_b\) also has derivative unity at its fixed point \(L=\mathrm e\approx 2.718\) |
| − | The general claim is that through the [[Cauchi integral]] or with [[redular iteration]] of with its modification, the [[superfunction]] and the corresponding [[Abel function]] can be implemented for any reasonable holomorphic transfer function. Case |
+ | The general claim is that through the [[Cauchi integral]] or with [[redular iteration]] of with its modification, the [[superfunction]] and the corresponding [[Abel function]] can be implemented for any reasonable holomorphic transfer function. Case \(T=\mathrm{zex}\) is important example of the transfer [[function]], for which the construction of superfunction seemed to be difficult, because at the fixed point of the transfer function its derivative is unity. |
==References== |
==References== |
||
Latest revision as of 18:44, 30 July 2019
Auzex is inverse function of SuZex; \(\mathrm{AuZex} = \mathrm{SuZex}^{-1}\)
AuZex is also Abel function for the transfer function \(\mathrm{zex}(z)=z \exp(z)\).
Contents
Basic properties
AuZex is Inverse function of SuZex, so, in wide ranges of values of \(z\), the relations
(1) \( ~ ~ ~ {\rm SuZex}\Big( \mathrm{AuZex}(z) \Big) = z \)
and
(2) \( ~ ~ ~ \mathrm{AuZex}\Big( \mathrm{SuZex}(z) \Big) = z \)
hold. In particular, \(~\mathrm{AuZex}(1)=0\).
Also, AuZex satisfies the Abel equation
(3) \( ~ ~ ~ \mathrm{AuZex}\Big( \mathrm{zex}(z) \Big) = \mathrm{AuZex}(z) +1\)
in this case, zex appears as transfer function, and AuZex is its Abel function. Iterations of equation (3) gives the relations
(4) \( ~ ~ ~ \mathrm{AuZex}\Big( \mathrm{zex}^n(z) \Big) = \mathrm{AuZex}(z) +n\)
This can be re-writtern also as
(5) \( ~ ~ ~ \mathrm{AuZex}\Big( \mathrm{LambertW}^n(z) \Big) = \mathrm{AuZex}(z) - n\)
as LambertW is inverse function of zex.
The relations above indicate ways to construct the efficient approximation of AuZex, covering the whole complex plane, and make the efficient (fast and precise) implementation. These approximations are described in the special article AuZex Approximation.
About the name
There is difficult question about choosing of the name of function.
The name should be short, in order to allow its use in an expression that fits the one-line equation.
The should be unique, in order to avoid confusion with other functions, while all figures are collected in the same directory for some article or book, or just
two different functions are used in the same expression.
The name should be easy to remember, in order to have no need to copypast it from the description page each time of the use.
The First letter "A" may refer to ArcSuZex or to Abel function, as AuZex is inverse function of SuZex and Abel function of zex, \(\mathrm{zex}(z)=z\exp(z)\).
The second letter "u" may indicate that upper side of the coordinate plane is used for the plot of the SuZex. For real values of the argument \(x\), Suzex\((x)\!>\!0\).
The letter "d" may be used to create names SdZex and its inverse function AdZex for the other superfunction and Abel function of zex, of as soon as these functions will be requested, implemented and loaded to TORI.
Any other suggestions for the naming of these functions should be appreciated.
Fixed point of Zex
AuZex is Abel function for the transfer function \(T\!=\,\)zex, which has the only one real fixed point \(L\!=\!0\). Aiming applications to the physics and, in particular, to the Laser science, the real superfunctions and Abel functions are of special interest. This refers not namely zex as a transfer function for some strange amplifier, but the method of constructing of real superfunctions and Abel functions; the real functions are more likely to be used in physical applications than those that have complex values along the real axis. For this reason, namely this fixed point is chosen as asymptotic value of SuZex at minus infinity. Correspondently, its inverse function AuZex has singularity at zero.
The fixed point of the transfer function can be used for the expansion of the Abel function. For the transfer function zex, the expansion of the Abel function begins with minus first power and logarithmic terms:
(6) \(~ ~ ~ \displaystyle \mathrm{AuZex}(z) \approx \frac{-1}{z}+\frac{1}{2}\ln(z)+\sum_{n=0}^N ~ c_n z^n\)
The series does not seem to converge; the more terms are taken into account, the narrower is the range of the approximation. However, for small \(|z|\), this expansion can be used for the fast and precise evaluation. Similar situation takes place with expansion of ArcTetration at the fixed points \(L\) and \(L^*\) of the exponential; at the increase of precision or at the attempts to extend the range of the approximation, some additional terms (not specified in (6)) become significant.
The expansion at fixed point zero provides of orderor of 15 decimal digits for \(N=12\) at \(|z|<0.1\)
Example of the "regular iteration"
Similar approach is used to implement two Abel functions of the exponential to to base \(b=\exp^2(-1)=\exp(1/\mathrm e)\approx 1.444667861\) [1]. In that case, the transfer function \(\exp_b\) also has derivative unity at its fixed point \(L=\mathrm e\approx 2.718\)
The general claim is that through the Cauchi integral or with redular iteration of with its modification, the superfunction and the corresponding Abel function can be implemented for any reasonable holomorphic transfer function. Case \(T=\mathrm{zex}\) is important example of the transfer function, for which the construction of superfunction seemed to be difficult, because at the fixed point of the transfer function its derivative is unity.
References
- ↑ http://tori.ils.uec.ac.jp/PAPERS/2012e1eMcom2590.pdf H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). Mathematics of Computation, 2012 February 8. ISSN 1088-6842(e) ISSN 0025-5718(p)
Keywords
AuZex, Abel function, LambertW, LambertW.cin, Superfunction, Zex