File:Analuxp01u400.jpg
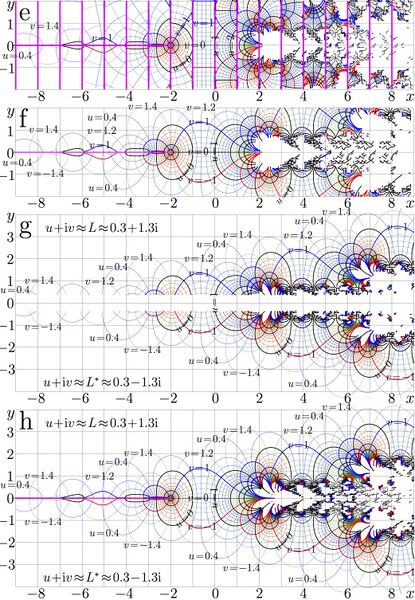
Complex maps of various approximations $f$ of natural tetration.
$u+\mathrm i v=f(x\!+\!\mathrm i y)$
Note, that in the Book Суперфункции, the same map is shown in a different way, $u$ means logamplitude and $v$ means phase there, the lines are shown for $\exp(u+\mathrm i v)=f(x\!+\!\mathrm i y)$. I do not know which notation is better.
Contents
Description of curves
e: Linear approximation by Gusmad
This is approximation, linear in the ramge $-1 < \Re(z) \le 0$ suggested in 2006 by M.H.Hooshmand [1]
$u+\mathrm i v=\mathrm{uxp}(x\!+\!\mathrm i y)$
$\mathrm{uxp}(z)=\!\left\{\!\!\!\! \begin{array}{ccccc cc} \ln\!\big({\rm uxp}(z\!+\!1)\big)~&~{\rm at}~&~ \!&\! \!&\! \Re(z) \!&\! \le \!&\! -1 \\ z + 1 ~&{~\rm at}~&~ -1 \!&\! < \!&\! \Re(z) \!&\! \le \!&\! 0 \\ \exp\!\big({\rm uxp}(z\!-\!1)\big)~&{~\rm at}~&~ 0 \!&\! < \!&\! \Re(z) \!& \end{array} \right.$
f: Approximation for moderate values of imaginary part of the argument
$\mathrm {Fit}_{3}(z) = \left\{\!\! \begin{array}{ccccc cc} \ln\!\big({\rm Fit}_{3}(z\!+\!1)\big)~&~{~\rm at~}~&~ \!&\! \!&\! \Re(z) \!&\! \le \!&\! -1 \\ \mathrm{fit}_{3}(z) ~&~{~\rm at~}~& -1 \!&\! < \!&\! \Re(z) \!&\! \le \!&\! 0 \\ \exp\!\big({\rm Fit}_{3}(z\!-\!1)\big)~&~{~\rm at~}~&~ 0 \!&\! < \!&\! \Re(z) \!& \end{array} \right. $
where
$\displaystyle \mathrm{fit}_3(z) \!=\! 0.6\!~\mathrm{fit}_{2}(z)+0.4\!~\ln\big( \mathrm{fit}_{2}(z+1)\big) $
$\displaystyle \mathrm{fit}_2(z) \!=\! \ln(2\!+\!z) + (1\!+\!z)\left(
1 +
\frac{z}{2}\exp\!\Big((z\!-\!1)s_2(z)\Big)
\Big(\!\mathrm e\! -2\! +\! \ln\frac{4}{3} \Big)
- \ln 2
\right)$
$ s_2(z) = \exp\!\Big(\exp(z-2.51)\Big)-0.6+0.08(z\!+\!1) $
g. Approximation for large values of imaginary part of the argument
In the upper half plane, say, $y>1/2$, the $\mathrm{fit}_6$ is shown,
$u+\mathrm i v =\mathrm{fit}_6(x\!+\!\mathrm i y)$
where
$\mathrm{fit}_6(z) = \left\{ \begin{array} ~ L+\exp(kz+r) ~, ~ \Re(z)<-8\\ \exp\Big(\mathrm{fit}_6(z\!-\!1)\Big)~,~ \Re(z)\ge -8 \end{array} \right.$
and
$u+\mathrm i v =\mathrm{fit}_6(x\!-\!\mathrm i y)^*$
in the lower half plane, say, $y<-1/2$.
The strip of intermediate values $|y|<1/2$ is left empty.
In formula above, $L\approx 0.31813150520476413 + 1.3372357014306895 \,\mathrm i$ is fixed point of logarithm, $L=\ln(L)$. For Natural tetration, the increment $k=L$. Parameter $r$ provides the match of the two asymptotics. It is fundamental mathematical constant; $r \approx 1.075820830781 - 0.9466419207254 \, \mathrm i$ . This precision seems to be sufficient for the applications; however, the improvement of the precision may be subject of the additional research.
h. Precise approximation.
The precise approximation of the natural tetration, with 14 decimal digits, is described at [2][3]. is this text seen? is this text seen?
$u+\mathrm i v=\mathrm{tet}(x\!+\!\mathrm i y)$
However, looking at the picture. it is not possible to guess, which algorithm is used, the direct implementation of the Cauchi integral [2]
or the fast implementation by [3], as the deviation is of order of $10^{-14}$; the precision greatly exceeds the needs of the graphical illustration of the function.
Similar images and motivation
The similar image appears as Figure 1 in the First publication about real-holomorphic natural tetration [2], but there, the logamplitud and phase are shown instead of real and imaginary parts; in certain sense this is equivalent of displacement of the map to the right for unity.
The reason of the derailed description of so simple image is historic. Many colleagues are interested in history of physics and mathematics; and they asked me, how did I guess the asymptotic behaviour of the natural titration at $\mathrm i \infty$. The last request was in 2013 by Michael Moldenhauer [4].
Functions $\mathrm{fit}_2$ and $\mathrm{fit}_3$ above provide the key. I used to check many fits. The $\mathrm{fit}_2$ and $\mathrm{Fit}_3$ happened best to see the asymtotics.
In order not to repeat the same explanation again and again, I load the generators and, in particular, the code that includes $\mathrm{fit}_3$ above. One can begin with $\mathrm{fit}_2$ and see, that the simple fit can provide the camera-ready pictures at least in vicinity of the real axis. This fit is already sufficient to see the asymptotics with naked eyes. The $\mathrm{fit}_3$ and $\mathrm{Fit}_3$ were arranged to confirm the guess: the better is the approximation of tetration, the closer does it approach to the asymptotics.
After to postulate the asymptotic behaviour of the tetration, it is not difficult to construct the algorithm for the precise evaluation. The Cauchi integral along the contour $|\Re(z)|=1$ is simple straightforward way; perhaps, there exist other, even more efficient algorithms.
C++ generators of curves. picture e, the top
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
#include <complex.h>
#define z_type complex<double>
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
//#include "uxp.cin"
//#include "advacon.cin"
#include "conto.cin"
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
//z_type Zo=z_type(.31813150520476413, 1.3372357014306895);
//z_type Zc=z_type(.31813150520476413,-1.3372357014306895);
int K=200,K1=K+1;
DB A=10.; DB dy=2*A/K; printf("dy=%6.3f",dy);
#define Y(k) (dy*(k-K/2))
printf("y_0=%6.3f y_K=%6.3f ",Y(0), Y(K));
int M=180,M1=M+1;
int N=50,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
// z_type tm,tp,F[M1*N1];
z_type tm,tp,F[9681];
//char v[11000]; // v is working array
// printf("Output fig01a.eps\n");
FILE *o;o=fopen("analuxp01e.eps","w");ado(o,364,84);
fprintf(o,"182 42 translate\n 20 20 scale\n");
//DB sy=4.3/sinh(.04*N/2.);
DB sy=2/sinh(.04*N/2.);
DO(m,M1) X[m]=-9.+.1*(m+.5);
DO(n,N1) Y[n]=sy*sinh(.04*(n+.5-N/2));
//for(m=-10;m<9;m++) {M(m,-4)L(m,4)}
for(m=-9;m<10;m++) {M(m,-2)L(m,2)}
for(n=-2;n<3;n++) {M(-9,n)L(9,n)} fprintf(o,".006 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){
g[m*N1+n]=9999;
f[m*N1+n]=9999;
}
//for(m=96;m<106;m++){x=X[m];
//for(m=95;m<106;m++){x=X[m];
for(m=80;m<90;m++){x=X[m];
DO(n,N1){y=Y[n]; z=z_type(x,y);
// c=z+1.;
F[m*N1+n]=z+1.; p=Re(z); q=Im(z);
// if(p>-999 && p<999) g[m*N1+n]=p;
// if(q>-999 && q<999) f[m*N1+n]=q;
}
}
for(m=90;m<M1;m++)
DO(n,N1)
{
F[m*N1+n] = exp( F[(m-10)*N1+n] );
}
for(m=79;m>=0;m--)
DO(n,N1)
{
F[m*N1+n] = log( F[(m+10)*N1+n] );
}
DO(m,M1)
DO(n,N1){
c=F[m*N1+n]; p=Re(c); q=Im(c);
if(p>-99 && p<99) g[m*N1+n]=p;
if(q>-99 && q<99) f[m*N1+n]=q;
}
p=1;
conto(o,f,w,v,X,Y,M,N, (-4 ),-5,5); fprintf(o,".04 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( -3 ),-5,5); fprintf(o,".04 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-3.+.1*n),-p, p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-2. ),-2 ,2); fprintf(o,".03 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-2.+.1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-1. ),-2 ,2); fprintf(o,".03 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-1.+.1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-5,5); fprintf(o,".02 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( .1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 1. ),-2 ,2); fprintf(o,".03 W 0 0 1 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( 1.+.1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 2. ),-2 ,2); fprintf(o,".03 W 0 0 1 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( 2.+.1*n),-p, p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 3 ),-5,5); fprintf(o,".04 W 0 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 4 ),-5,5); fprintf(o,".04 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-2. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (-2.+.1*n),-p,p); fprintf(o,".01 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-1. ),-2,2); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (-1.+.1*n),-p,p); fprintf(o,".01 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (0. ),-3,3); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( .1*n),-p,p); fprintf(o,".01 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 1. ),-2,2); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( 1.+.1*n),-p,p); fprintf(o,".01 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 2. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 3. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 4. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
for(m=-10;m<9;m++) {M(m,-2.)L(m,2.)}
M(-10,0)L(-2,0)fprintf(o,".06 W 1 0 1 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf analuxp01e.eps");
system( "open analuxp01e.pdf");
getchar();
system("killall Preview");
}
C++ generators of curves. Picture f
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
#include <complex.h>
#define z_type complex<double>
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "analuxpf3c.cin"
#include "conto.cin"
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
//z_type Zo=z_type(.31813150520476413, 1.3372357014306895);
//z_type Zc=z_type(.31813150520476413,-1.3372357014306895);
int K=200,K1=K+1;
DB A=10.; DB dy=2*A/K; printf("dy=%6.3f",dy);
#define Y(k) (dy*(k-K/2))
printf("y_0=%6.3f y_K=%6.3f ",Y(0), Y(K));
int M=179,M1=M+1;
int N=51,N1=N+1;
// z_type tm,tp,F[M1*N1]; does not work
z_type tm,tp,F[180*52];
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
// printf("Output fig01b.eps\n");
FILE *o;o=fopen("analuxp01f.eps","w");ado(o,364,84);
fprintf(o,"182 42 translate\n 20 20 scale\n");
//DB sy=4.3/sinh(.04*N/2.);
DB sy=2/sinh(.04*N/2.);
DO(m,M1) X[m]=-9.+.1*(m-.5);
DO(n,N1) Y[n]=sy*sinh(.04*(n-.5-N/2));
//for(m=-10;m<9;m++) {M(m,-4)L(m,4)}
for(m=-9;m<10;m++) {M(m,-2)L(m,2)}
for(n=-2;n<3;n++) {M(-9,n)L(9,n)} fprintf(o,".006 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){
g[m*N1+n]=9999;
f[m*N1+n]=9999;
}
//for(m=96;m<106;m++){x=X[m];
//for(m=95;m<106;m++){x=X[m];
for(m=81;m<91;m++){x=X[m];
DO(n,N1){y=Y[n]; z=z_type(x,y);
// c=z+1.;
c=f3(z);
F[m*N1+n]=c; p=Re(c); q=Im(c);
// if(p>-999 && p<999) g[m*N1+n]=p;
// if(q>-999 && q<999) f[m*N1+n]=q;
}
}
for(m=91;m<M1;m++)
DO(n,N1)
{
F[m*N1+n] = exp( F[(m-10)*N1+n] );
}
for(m=80;m>=0;m--)
DO(n,N1)
{
F[m*N1+n] = log( F[(m+10)*N1+n] );
}
DO(m,M1)
DO(n,N1){
c=F[m*N1+n]; p=Re(c); q=Im(c);
if(p>-999 && p<999) g[m*N1+n]=p;
if(q>-999 && q<999) f[m*N1+n]=q;
}
p=.8;
conto(o,f,w,v,X,Y,M,N, ( -4 ),-4, 4); fprintf(o,".04 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( -3 ),-4, 4); fprintf(o,".04 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-3.+.1*n),-p, p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-2. ),-2 ,2); fprintf(o,".03 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-2.+.1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-1. ),-2 ,2); fprintf(o,".03 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-1.+.1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-4, 4); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( .1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 1. ),-2 ,2); fprintf(o,".03 W 0 0 1 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( 1.+.1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 2. ),-2 ,2); fprintf(o,".03 W 0 0 1 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( 2.+.1*n),-p, p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 3 ),-4, 4); fprintf(o,".04 W 0 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 4 ),-4, 4); fprintf(o,".04 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-2. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (-2.+.1*n),-p,p); fprintf(o,".01 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-1. ),-1,1); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (-1.+.1*n),-p,p); fprintf(o,".01 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (0. ),-4,4); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( .1*n),-p,p); fprintf(o,".01 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 1. ),-1,1); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( 1.+.1*n),-p,p); fprintf(o,".01 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 2. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 3. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 4. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
M(-10,0)L(-2,0)fprintf(o,".04 W 1 0 1 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf analuxp01f.eps");
system( "open analuxp01f.eps");
getchar();
system("killall Preview");
}
C++ generators of curves. Picture g
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
#include <complex.h>
#define z_type complex<double>
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
//#include "f4c.cin"
#include "conto.cin"
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
z_type Zo=z_type(.31813150520476413, 1.3372357014306895);
z_type Zc=z_type(.31813150520476413,-1.3372357014306895);
z_type T =2*M_PI/Zo;
//z_type r=z_type(1.06,-.96);
z_type r=z_type(1.075820830781, - 0.9466419207254);
int K=200,K1=K+1;
DB A=10.; DB dy=2*A/K; printf("dy=%6.3f",dy);
#define Y(k) (dy*(k-K/2))
printf("y_0=%6.3f y_K=%6.3f ",Y(0), Y(K));
int M=180,M1=M+1;
int N=80,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
//z_type tm,tp,F[M1*N1];
z_type tm,tp,F[181*81];
// printf("Output fig01c.eps\n");
FILE *o;o=fopen("analuxp01g.eps","w");ado(o,364,204);
fprintf(o,"182 102 translate\n 20 20 scale\n");
DB sy=4.3/sinh(.04*N/2.);
DO(m,M1) X[m]=-9+.1*m;
DO(n,N1) Y[n]=sy*sinh(.04*(n-N/2));
for(m=-9;m<10;m++) {M(m,-4)L(m,4)}
for(n=-4;n<5;n++) {M( -9,n)L(9,n)} fprintf(o,".006 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){
g[m*N1+n]=9999;
f[m*N1+n]=9999;
}
for(m=0;m<10;m++){int m1; x=X[m];
DO(n,N1){y=Y[n]; z=z_type(x,y); //c=F4(z-1.);
if(y>.3) c=Zo+exp(Zo*(z)+r);
else
if(y<-.3) c=Zc+exp(Zc*(z)+conj(r));
//z_type(0.318131505204764, 1.337235701430689)
else goto ski;
// int m1;
for(m1=m;m1<M1;){ F[m1*N1+n]=c; p=Re(c); q=Im(c);
if(p>-999 && p<999) g[m1*N1+n]=p;
if(q>-999 && q<999) f[m1*N1+n]=q;
c=exp(c); m1+=10;
}
ski:;
}
}
/*
DO(m,M1)
DO(n,N1){
c=F[m*N1+n]; p=Re(c); q=Im(c);
if(p>-999 && p<999) g[m*N1+n]=p;
if(q>-999 && q<999) f[m*N1+n]=q;
}
*/
p=2;
conto(o,f,w,v,X,Y,M,N, ( -4. ),-999,999); fprintf(o,".04 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( -3. ),-999,999); fprintf(o,".04 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-3.+.1*n),-p, p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-2. ),-9 ,9); fprintf(o,".03 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-2.+.1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-1. ),-9 ,9); fprintf(o,".03 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-1.+.1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-999,999); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( .1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 1. ),-9 ,9); fprintf(o,".03 W 0 0 1 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( 1.+.1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 2. ),-9 ,9); fprintf(o,".03 W 0 0 1 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( 2.+.1*n),-p, p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 3. ),-999,999); fprintf(o,".04 W 0 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 4. ),-999,999); fprintf(o,".04 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-2. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (-2.+.1*n),-p,p); fprintf(o,".01 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-1. ),-3,3); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (-1.+.1*n),-p,p); fprintf(o,".01 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (0. ),-999,999); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( .1*n),-p,p); fprintf(o,".01 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 1. ),-3,3); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( 1.+.1*n),-p,p); fprintf(o,".01 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 2. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 3. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 4. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
//M(-10,0)L(-2,0)fprintf(o,".04 W 1 0 1 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
//system( "ggv fig01c.eps");
system("epstopdf analuxp01g.eps");
system( "open analuxp01g.eps");
getchar();
system("killall Preview");
}
C++ generators of curves. Picture h
// file analuxpf4c.cin
<nomathjax>
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
#include <complex.h>
#define z_type complex<double>
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "analuxpf4c.cin"
#include "conto.cin"
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
z_type Zo=z_type(.31813150520476413, 1.3372357014306895);
z_type Zc=z_type(.31813150520476413,-1.3372357014306895);
int K=200,K1=K+1;
DB A=10.; DB dy=2*A/K; printf("dy=%6.3f",dy);
#define Y(k) (dy*(k-K/2))
printf("y_0=%6.3f y_K=%6.3f ",Y(0), Y(K));
int M=180,M1=M+1;
int N=80,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
//z_type tm,tp,F[M1*N1];
z_type tm,tp,F[181*81];
char v[M1*N1]; // v is working array
// printf("Output fig01d.eps\n");
FILE *o;o=fopen("analuxp01h.eps","w");ado(o,364,204);
fprintf(o,"182 102 translate\n 20 20 scale\n");
DB sy=4.3/sinh(.04*N/2.);
DO(m,M1) X[m]=-9.+.1*m;
DO(n,N1) Y[n]=sy*sinh(.04*(n-N/2));
for(m=-9;m<10;m++) {M(m,-4)L(m,4)}
for(n=-4;n<5;n++) {M( -9,n)L(9,n)} fprintf(o,".006 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){
g[m*N1+n]=9999;
f[m*N1+n]=9999;
}
//for(m=96;m<106;m++){x=X[m];
//for(m=90;m<100;m++){x=X[m];
for(m=86;m<96;m++){x=X[m];
DO(n,N1){y=Y[n]; z=z_type(x,y);
c=F4(z);
F[m*N1+n]=c; p=Re(c); q=Im(c);
if(p>-999 && p<999) g[m*N1+n]=p;
if(q>-999 && q<999) f[m*N1+n]=q;
}
}
for(m=96;m<M1;m++)
DO(n,N1)
{
F[m*N1+n] = exp( F[(m-10)*N1+n] );
}
for(m=85;m>=0;m--)
DO(n,N1)
{
F[m*N1+n] = log( F[(m+10)*N1+n] );
}
DO(m,M1)
DO(n,N1){
c=F[m*N1+n]; p=Re(c); q=Im(c);
if(p>-999 && p<999) g[m*N1+n]=p;
if(q>-999 && q<999) f[m*N1+n]=q;
}
p=2;
conto(o,f,w,v,X,Y,M,N, (-4 ),-999,999); fprintf(o,".04 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( -3 ),-999,999); fprintf(o,".04 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-3.+.1*n),-p, p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-2. ),-9 ,9); fprintf(o,".03 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-2.+.1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-1. ),-9 ,9); fprintf(o,".03 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-1.+.1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-999,999); fprintf(o,".02 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( .1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 1. ),-9 ,9); fprintf(o,".03 W 0 0 1 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( 1.+.1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 2. ),-9 ,9); fprintf(o,".03 W 0 0 1 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( 2.+.1*n),-p, p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 3 ),-99,99); fprintf(o,".04 W 0 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 4 ),-99,99); fprintf(o,".04 W 0 0 1 RGB S\n");
// conto(o,f,w,v,X,Y,M,N, ( M_PI ),-99,99); fprintf(o,".04 W 1 0 1 RGB S\n");
// conto(o,f,w,v,X,Y,M,N, (3*M_PI ),-99,99); fprintf(o,".04 W 1 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-2. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (-2.+.1*n),-p,p); fprintf(o,".01 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-1. ),-3,3); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (-1.+.1*n),-p,p); fprintf(o,".01 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (0. ),-99,99); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( .1*n),-p,p); fprintf(o,".01 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 1. ),-3,3); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( 1.+.1*n),-p,p); fprintf(o,".01 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 2. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 3. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 4. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
M(-10,0)L(-2,0)fprintf(o,".04 W 1 0 1 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
//system( "ggv fig01d.eps");
system("epstopdf analuxp01h.eps");
system( "open analuxp01h.eps");
getchar();
system("killall Preview");
}
<nomathjax>
C++ generators of curves. Picture i
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
#include <complex.h>
#define z_type complex<double>
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
//#include "analuxpf4c.cin"
#include "fsexp.cin"
#include "conto.cin"
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
z_type Zo=z_type(.31813150520476413, 1.3372357014306895);
z_type Zc=z_type(.31813150520476413,-1.3372357014306895);
int K=200,K1=K+1;
DB A=10.; DB dy=2*A/K; printf("dy=%6.3f",dy);
#define Y(k) (dy*(k-K/2))
printf("y_0=%6.3f y_K=%6.3f ",Y(0), Y(K));
int M=180,M1=M+1;
int N=160,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
//z_type tm,tp,F[M1*N1];
z_type tm,tp,F[181*161];
char v[M1*N1]; // v is working array
// printf("Output fig01d.eps\n");
FILE *o;o=fopen("analuxp01i.eps","w");ado(o,364,204);
fprintf(o,"182 102 translate\n 20 20 scale\n");
DB sy=4.3/sinh(.02*N/2.);
DO(m,M1) X[m]=-9.+.1*m;
DO(n,N1) Y[n]=sy*sinh(.02*(n-.5-N/2));
for(m=-9;m<10;m++) {M(m,-4)L(m,4)}
for(n=-4;n<5;n++) {M( -9,n)L(9,n)} fprintf(o,".006 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){
g[m*N1+n]=9999;
f[m*N1+n]=9999;
}
//for(m=96;m<106;m++){x=X[m];
//for(m=90;m<100;m++){x=X[m];
for(m=86;m<96;m++){x=X[m];
DO(n,N1){y=Y[n]; z=z_type(x,y);
//c=F4(z);
c=FSEXP(z);
F[m*N1+n]=c; p=Re(c); q=Im(c);
if(p>-999 && p<999) g[m*N1+n]=p;
if(q>-999 && q<999) f[m*N1+n]=q;
}
}
for(m=96;m<M1;m++)
DO(n,N1)
{
F[m*N1+n] = exp( F[(m-10)*N1+n] );
}
for(m=85;m>=0;m--)
DO(n,N1)
{
F[m*N1+n] = log( F[(m+10)*N1+n] );
}
DO(m,M1)
DO(n,N1){
c=F[m*N1+n]; p=Re(c); q=Im(c);
if(p>-999 && p<999) g[m*N1+n]=p;
if(q>-999 && q<999) f[m*N1+n]=q;
}
p=2;
conto(o,f,w,v,X,Y,M,N, (-4 ),-999,999); fprintf(o,".04 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( -3 ),-999,999); fprintf(o,".04 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-3.+.1*n),-p, p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-2. ),-9 ,9); fprintf(o,".03 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-2.+.1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-1. ),-9 ,9); fprintf(o,".03 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-1.+.1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-999,999); fprintf(o,".02 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( .1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 1. ),-9 ,9); fprintf(o,".03 W 0 0 1 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( 1.+.1*n),-p ,p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 2. ),-9 ,9); fprintf(o,".03 W 0 0 1 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( 2.+.1*n),-p, p); fprintf(o,".01 W 0 .6 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 3 ),-99,99); fprintf(o,".04 W 0 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 4 ),-99,99); fprintf(o,".04 W 0 0 1 RGB S\n");
// conto(o,f,w,v,X,Y,M,N, ( M_PI ),-99,99); fprintf(o,".04 W 1 0 1 RGB S\n");
// conto(o,f,w,v,X,Y,M,N, (3*M_PI ),-99,99); fprintf(o,".04 W 1 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-2. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (-2.+.1*n),-p,p); fprintf(o,".01 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-1. ),-3,3); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (-1.+.1*n),-p,p); fprintf(o,".01 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (0. ),-99,99); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( .1*n),-p,p); fprintf(o,".01 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 1. ),-3,3); fprintf(o,".03 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( 1.+.1*n),-p,p); fprintf(o,".01 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 2. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 3. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 4. ),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
M(-10,0)L(-2,0)fprintf(o,".04 W 1 0 1 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
//system( "ggv fig01d.eps");
system("epstopdf analuxp01i.eps");
system( "open analuxp01i.eps");
getchar();
system("killall Preview");
}
Latex generator of labels
\documentclass[12pt]{article}
\usepackage{geometry}
\usepackage{graphics}
\usepackage{rotating}
\paperwidth 375px
\paperheight 542px
\textwidth 500pt
\textheight 900pt
\topmargin -100pt
\oddsidemargin -66pt
\parindent 0pt
\pagestyle{empty}
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\begin{document}
\sx{1.}{\begin{picture}(370,80)
%\put(5,5){\includegraphics{fig01a}}
\put(6,6){\includegraphics{analuxp01e}}
\put(11,71){\sx{2}{e}}
\put( 0,82){\sx{1.2}{$y$}}
\put( 0,63){\sx{1.1}{$1$}}
\put( 0,43){\sx{1.1}{$0$}}
\put(-9,23){\sx{1.1}{$-1$}}
\put( 18,-2){\sx{1.1}{$-8$}}
\put( 58,-2){\sx{1.1}{$-6$}}
\put(98,-2){\sx{1.1}{$-4$}}
\put(138,-2){\sx{1.1}{$-2$}}
\put(186,-2){\sx{1.1}{$0$}}
\put(226,-2){\sx{1.1}{$2$}}
\put(266,-2){\sx{1.1}{$4$}}
\put(306,-2){\sx{1.1}{$6$}}
\put(346,-2){\sx{1.1}{$8$}}
\put(362,-2){\sx{1.2}{$x$}}
\put(-4,36){\sx{.8}{$u\!=\!0.4$}}
\put(156,56){\sx{.8}{\rot{56}{$v\!=\!1$}\ero}}
\put(152,24){\sx{.8}{\rot{32}{$u\!=\!0$}\ero}}
\put(21,63){\sx{.8}{$v\!=\!1.4$}}
\put(77,52){\sx{.8}{$v\!=\!1$}}
%\put(169,85.6){\sx{.8}{\rot{0.}{$v\!=\!2$}\ero}}
\put(169,65.6){\sx{.8}{\rot{0.}{$v\!=\!1$}\ero}}
\put(161,45.6){\sx{.8}{\rot{0.}{$v\!=\!0$}\ero}}
%\put(170,25){\sx{.8}{\rot{0.}{$v\!=\!-1$}\ero}}
\put(192,38){\sx{.8}{\rot{90}{$u\!=\!1$}\ero}}
\put(206,38){\sx{.8}{\rot{90}{$u\!=\!2$}\ero}}
\end{picture}}
\sx{1.}{\begin{picture}(370,96)
\put( 6,6){\includegraphics{analuxp01f}}
\put(11,71){\sx{2}{f}}
\put( 0,82){\sx{1.2}{$y$}}
\put( 0,63){\sx{1.1}{$1$}}
\put( 0,43){\sx{1.1}{$0$}}
\put(-9,23){\sx{1.1}{$-1$}}
\put( 18,-2){\sx{1.1}{$-8$}}
\put( 58,-2){\sx{1.1}{$-6$}}
\put( 98,-2){\sx{1.1}{$-4$}}
\put(138,-2){\sx{1.1}{$-2$}}
\put(186,-2){\sx{1.1}{$0$}}
\put(226,-2){\sx{1.1}{$2$}}
\put(266,-2){\sx{1.1}{$4$}}
\put(306,-2){\sx{1.1}{$6$}}
\put(346,-2){\sx{1.1}{$8$}}
\put(362,-2){\sx{1.2}{$x$}}
\put(-4,36){\sx{.8}{$u\!=\!0.4$}}
\multiput(20,66)(90,21){2}{\sx{.8}{$v\!=\!1.4$}}
\multiput(73,77)(-90,-21){1}{\sx{.8}{$u\!=\!0.4$}}
\multiput(163,86)(-90,-21){2}{\sx{.8}{$v\!=\!1.2$}}
\multiput(165,73)(-90,-21){2}{\sx{.8}{$v\!=\!1$}}
\put(164,46){\sx{.8}{$v\!=\!0$}}
\put(164,20){\sx{.8}{$v\!=\!-1$}}
\multiput(157,21)(90,-20.6){2}{\sx{.8}{\rot{46}{$u\!=\!0$}\ero}}
\put(191,39){\sx{.8}{\rot{90}{$u\!=\!1$}\ero}}
\multiput(74,13)(90,-21){1}{\sx{.8}{$u\!=\!0.4$}}
\multiput(18,26)(90,-21){1}{\sx{.8}{$v\!=\!-1.4$}}
\end{picture}}
\sx{1.}{\begin{picture}(366,176)
\put( 6,-14){\includegraphics{analuxp01g}}
\put(35,153){\sx{1.}{$u\!+\!\mathrm i v \!\approx\! L\!\approx\! 0.3\!+\!1.3\mathrm i$}}
\put(33,13){\sx{1.}{$u\!+\!\mathrm i v \!\approx\! L^*\!\approx\! 0.3\!-\!1.3\mathrm i$}}
\put(11,152){\sx{2}{g}}
\put( 0,164){\sx{1.2}{$y$}}
\put( 0,144){\sx{1.1}{$3$}}
\put( 0,124){\sx{1.1}{$2$}}
\put( 0,104){\sx{1.1}{$1$}}
\put( 0, 84){\sx{1.1}{$0$}}
\put(-9, 64){\sx{1.1}{$-1$}}
\put(-9, 44){\sx{1.1}{$-2$}}
\put(-9, 24){\sx{1.1}{$-3$}}
\put( 18,-2){\sx{1.1}{$-8$}}
\put( 58,-2){\sx{1.1}{$-6$}}
\put( 98,-2){\sx{1.1}{$-4$}}
\put(138,-2){\sx{1.1}{$-2$}}
\put(186,-2){\sx{1.1}{$0$}}
\put(226,-2){\sx{1.1}{$2$}}
\put(266,-2){\sx{1.1}{$4$}}
\put(306,-2){\sx{1.1}{$6$}}
\put(346,-2){\sx{1.1}{$8$}}
\put(362,-2){\sx{1.2}{$x$}}
\multiput(261,160)(-89,-20.8){4}{\sx{.8}{$u\!=\!0.4$}}
\multiput(251,147)(-90,-20.8){3}{\sx{.8}{$v\!=\!1.2$}}
\multiput(165,113)(90,20.8){3}{\sx{.8}{$v\!=\!1$}}
%\put(164,86){\sx{.8}{$v\!=\!0$}}
\multiput(164,60)(90,-20.8){3}{\sx{.8}{$v\!=\!-1$}}
\multiput(156,61)(90,-20.8){3}{\sx{.8}{\rot{44}{$u\!=\!0$}\ero}}
\put(191,79){\sx{.8}{\rot{90}{$u\!=\!1$}\ero}}
\multiput(16,106)(90,20.8){4}{\sx{.8}{$v\!=\!1.4$}}
\multiput(16,64)(90,-20.8){3}{\sx{.8}{$v\!=\!-1.4$}}
\multiput(75,54)(90,-20.8){3}{\sx{.8}{$u\!=\!0.4$}}
\end{picture}}
\sx{1.}{\begin{picture}(366,176)
\put( 6,-14){\includegraphics{analuxp01i}}
\put(35,153){\sx{1.}{$u\!+\!\mathrm i v \!\approx\! L\!\approx\! 0.3\!+\!1.3\mathrm i$}}
\put(33,13){\sx{1.}{$u\!+\!\mathrm i v \!\approx\! L^*\!\approx\! 0.3\!-\!1.3\mathrm i$}}
\put(11,151){\sx{2}{h}}
\put( 0,162){\sx{1.2}{$y$}}
\put( 0,144){\sx{1.1}{$3$}}
\put( 0,124){\sx{1.1}{$2$}}
\put( 0,104){\sx{1.1}{$1$}}
\put( 0, 84){\sx{1.1}{$0$}}
\put(-9, 64){\sx{1.1}{$-1$}}
\put(-9, 44){\sx{1.1}{$-2$}}
\put(-9, 24){\sx{1.1}{$-3$}}
\put( 18,-2){\sx{1.1}{$-8$}}
\put( 58,-2){\sx{1.1}{$-6$}}
\put( 98,-2){\sx{1.1}{$-4$}}
\put(138,-2){\sx{1.1}{$-2$}}
\put(186,-2){\sx{1.1}{$0$}}
\put(226,-2){\sx{1.1}{$2$}}
\put(266,-2){\sx{1.1}{$4$}}
\put(306,-2){\sx{1.1}{$6$}}
\put(346,-2){\sx{1.1}{$8$}}
\put(362,-2){\sx{1.2}{$x$}}
\multiput(261,160)(-89,-20.8){4}{\sx{.8}{$u\!=\!0.4$}}
%\multiput(251,159)(-90,-20.8){4}{\sx{.8}{$u\!=\!0.4$}}
\multiput(251,147)(-90,-20.8){3}{\sx{.8}{$v\!=\!1.2$}}
\multiput(165,113)(90,20.8){3}{\sx{.8}{$v\!=\!1$}}
\put(164,86){\sx{.8}{$v\!=\!0$}}
\multiput(164,60)(90,-20.8){3}{\sx{.8}{$v\!=\!-1$}}
\multiput(156,61)(90,-20.8){3}{\sx{.8}{\rot{44}{$u\!=\!0$}\ero}}
\put(191,79){\sx{.8}{\rot{90}{$u\!=\!1$}\ero}}
\multiput(16,106)(90,20.8){4}{\sx{.8}{$v\!=\!1.4$}}
\multiput(16,64)(90,-20.8){3}{\sx{.8}{$v\!=\!-1.4$}}
\multiput(75,54)(90,-20.8){3}{\sx{.8}{$u\!=\!0.4$}}
\end{picture}}
\end{document}
References
- ↑ 3. M.H.Hooshmand. ”Ultra power and ultra exponential functions”. Integral Transforms and Special Functions 17 (8), 549-558 (2006)
- ↑ 2.0 2.1 2.2
MOC
Cite error: Invalid
<ref>tag; name "analuxp" defined multiple times with different content Cite error: Invalid<ref>tag; name "analuxp" defined multiple times with different content - ↑ 3.0 3.1
Vladi
Cite error: Invalid
<ref>tag; name "vladi" defined multiple times with different content - ↑ Michael Moldenhauer. Question about tetration method. Private communication, Sat, 9 Nov 2013 01:11:53 -0800 (PST). .. how did you come up with the high-quality initial approximation "fit_3" mentioned in your paper about the tetrational function?
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 06:10, 1 December 2018 |  | 2,083 × 3,011 (1.72 MB) | Maintenance script (talk | contribs) | Importing image file |
- You cannot overwrite this file.
File usage
The following page links to this file: