Linear fraction

Linear fraction is meromorphic function that can be expressed with
\((1) ~ ~ ~ \displaystyle T(z)=\frac{u+v z}{w+z}\)
where \(u\), \(v\), \(w\) are parameters from the some set of numbers that allows operations of summation, multiplication and division. Usually, it is assumed, that they are complex numbers, and the operation of multiplication is commutative.
For case \(u\!=\!0\), \(v\!=\!-1\), \(w\!=0\), complex map of function \(T\) by (1) is shown in figure at right. Lines \(~u=\Re(T(x\!+\!\mathrm i y))=\mathrm {const}~\) and lines \(~v=\Im(T(x\!+\!\mathrm i y))=\mathrm {const}~\) are drawn with code conto.cin in the \((x,y)\) coordinate plane.
Linear function
Definition (1) excludes the case of linear function. However, this the linear function can be realized in limit
\((2) ~ ~ ~ \displaystyle A+B z= \lim_{M\rightarrow \infty} \frac{M A+ M B}{M+z}\)
where the expression of the function under the limit operation is expressed in a form that corresponds to (1), id est, \(u=M A\), \(v=MB\), \(w=M\).
Inverse function
The inverse function \(T^{-1}\) of the linear fraction \(T\) by (1) is also linear fraction, and its parameters can be easy expressed through the parameters of the initial linear fraction.
\((3) ~ ~ ~ \displaystyle T^{-1}(z)=\frac{u-w z}{-v+z}\)
One can easy check that \(T(T^{-1}(z))=T^{-1}(T(z))=z\) for all \(z\) excluding the poles, singularities at \(z=-w\) and at \(z=v\).
Linear conjugate of linear fraction
Linear conjugate of a function \(T\) is function \(Q\circ T\circ P\) where \(P\) is linear function and \(Q=P^{-1}\).
The linear function \(P\) can be parametrized with two parameters, \(A\) and \(B\), as follows:
\((4) ~ ~ ~ \displaystyle P(z)=A+B z\)
then
\((5) ~ ~ ~ \displaystyle Q(z)=(z-A)/B\)
and
\((6) ~ ~ ~ \displaystyle Q \circ T \circ P(z)= \frac{\frac{-A^2+A v-A w+u}{B^2}+\frac{v-A}{B} z}{\frac{A+w}{B}+z}\)
This form, at special choice of parameters \(A\) and \(B\) can be used in order to simplify the construction of non-integer iterates of the linear fraction. One of possible choices is
\((7) ~ ~ ~ \displaystyle \frac{v-A}{B}=1 ~ ~ \), \(~ ~ ~ \displaystyle -A^2+Av-Aw+u=0\)
and then
\((8) ~ ~ ~ \displaystyle A=\frac{v-w}{2}+r\)
\((9) ~ ~ ~ \displaystyle B=v-A=\frac{v+w}{2}-r\)
where
\((10) ~ ~ ~ \displaystyle r=\sqrt{\Big(\frac{v-w}{2}\Big)^2+u}\)
With such a choice,
\((11) ~ ~ ~ \displaystyle t(z)=Q \circ T \circ P(z)= \frac{z}{c+z}\)
where
\((12) ~ ~ ~ \displaystyle c=\frac{v+w+2r}{v+w-2r}\)
Then, the linear fraction \(T\) by (1) can be written as
\((13) ~ ~ ~ \displaystyle T(z)=P \circ t \circ Q(z)\)
and the \(n\)th iterate of \(T\) can be written as
\((14) ~ ~ ~ \displaystyle T^n(z)=P \circ t^n \circ Q(z)\)
Iterate of linear fraction
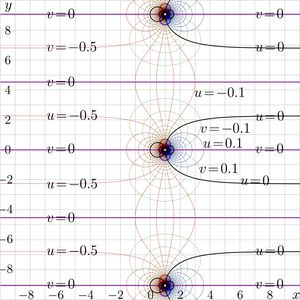

Iterate of the linear fraction or the special form \(t\) by ( 11) can be expressed as follows:
\((15) ~ ~ ~ \displaystyle t^n(z)=\frac{z}{c^n+\frac{1-c^n}{1-c} z }\)
Superfunction \(f\) for the transfer function \(t\) by (11) can be choosen as follows:
\((16) ~ ~ ~ \displaystyle f(z)=\frac{c-1}{c^z-c }\)
For \(c\!=\!2\), complex map of function \(f\) by (16) is shown in figure at right.
Superfunction \(f\) is periodic with period \(\displaystyle P=\frac{2 \pi \mathrm i}{\ln(c)} \)
For real values of \(c\) (and, in particular, for \(c=2\)), the period is pure imaginary.
At \(\Re(z)\rightarrow +\infty\), super function \(F(z)\) exponentially approaches zero.
At \(\Re(z)\rightarrow -\infty\), super function \(F(z)\) exponentially approaches constant \((1\!-\!c)/c\).
The corresponding Abel function \(t=g^{-1}\) can be expressed as follows:
\((17) ~ ~ ~ \displaystyle g(z)= \log_c\big(1+(c\!-\!1)/z \big)\)
For \(c\!=\!2\), complex map of function \(g\) by (17) is shown in figure.
With superfunction \(f\) by (16) and Abel function \(g\) by (17), the iterate of \(t\) can be written in the usual form
\((18) ~ ~ ~ \displaystyle t^n(z)=f(n+g(z))\)
note
Especially simple the interpretation of iteration of the transfer function \(T\) by (1) is for the case \(r\ge 0\), then, the \(T\) has at elast one real fixed point, and the \(n\)th iteration, id est, \(T^n\) is regular at this fixed point even at non-integer values of \(n\); the iteration also can be expressed as a linear fraction.
Superfunction of the linear fraction
The Iterate of linear fraction can be expressed through its superfunction and the Abel function; as usually, the additional conditions on the asymptotic behavior of these functions is required in order to make the non-integer iterate unique.
Keywords
Iterate of function, Superfunction, Holomorphic function
References
http://mathworld.wolfram.com/LinearFractionalTransformation.html