Iterate of linear fraction

$ t(z)=\frac{z}{0.5+z}~$; $~y=t^n(x)$ versus $x$ for various $n$

$ t(z)=\frac{z}{1+z} ~$; $~y=t^n(x)$ versus $x$ for various $n$

$ t(z)=\frac{z}{2+z} ~$; $~y=t^n(x)$ versus $x$ for various $n$

Iterate_of_linear_fraction (or iteration of linnet friaction) refers to function

(01)$~ ~ ~ \displaystyle T(z)=\frac{u+vz}{w+z}$

Iterate of a linear fraction can be expressed with also some linear fraction. This article describes this expression.

Special case

First, consider the special case when the iterated function has only single parameter. Let

(02) $~ ~ ~ \displaystyle t(z)=\frac{z}{c+z}$

where $c\ne 0$ is constant; for example, the real or complex number.

The iterate $t^n$ should satisfy the following equations:

$t^1(z)=t(z)$

$t^{m+n}(z)=t^m(t^n(z))$

For $c\ne 1$, the simple solution can be written as follows:

(03) $~ ~ ~ \displaystyle t^n(z)=\frac{z}{c^n+ \frac{1-c^n}{1-c} z }$

Limiting case

At $c=1$. The expression of the previous section cannot be applied as is. For this case, the $n$ th iteration of function $t(z)=\frac{z}{1+z}$ can be written as follows:

(04) $~ ~ ~ \displaystyle t^n(z)= $ $\displaystyle\lim_{c\rightarrow 1} $ $\displaystyle\frac{z}{c^n+ \frac{1-c^n}{1-c} z }=$ $\displaystyle\frac{z}{\displaystyle\lim_{s\rightarrow 0}\left( (1\!-\!s)^n + \frac{1-(1-s)^n}{s} z \right)}=$ $\displaystyle\frac{z}{1+nz}$

One can see that this expression satisfies equations

$ t^{n+1}(z)=t(t^n(z))=t^n(t(z))$

Generalization

Consider linear function $P$, let

(05) $~ ~ ~ \displaystyle P(z)=A + B z$

The inverse function can be written as follows:

(06) $~ ~ ~ \displaystyle Q(z)=P^{-1}(z)=\frac{x-A}{B}$

One can easy check that $P(Q(z))=Q(P(z))=z$. Let

(07) $~ ~ ~ \displaystyle T(z)=P(t(Q(z)))= \frac{ABc - AB - A^2 ~+~ (A\!+\!B)z}{Bc-A+z}$

This agree with equation (01) at

(08) $~ ~ ~ \displaystyle u=ABc-AB-A^2$

(09) $~ ~ ~ \displaystyle v=A+B$

(10) $~ ~ ~ \displaystyle w=Bc-A$

It is possible to express $A,B,c$ in terms of $u,v,w$:

(11) $~ ~ ~ \displaystyle A=\frac{v-w}{2} - r$

(12) $~ ~ ~ \displaystyle B=\frac{v+w}{2}+r$

(13) $~ ~ ~\displaystyle c=\frac{-2 u - v^2 - w^2 +(v+w) 2r}{2(u-vw)}$

where

(14) $~ ~ ~ \displaystyle r=\sqrt{u+\Big(\frac{v-w}{2}\Big)^2}$

In principle, it is possible to choose $r$ to be negative of the square root above. However, for the application in evaluation of the non-integer iterate, it is convenient to keep the coefficient $B$ positive, at least for positive $u,v,w$, in a wide range of their variation. In particular, the interpretation of transform $P$ is easier, while $P'(z)>0$.

Non-integer iterate

As function $g$ is expressed through conjugation of function $f$, the iteration can be expressed as follows:

(15) $~ ~ ~ \displaystyle T^n(z)=P(t^n(Q(z))$

All functions $P$, $t^n$ and $Q$ are defined above, and $f^n$ is expressed in a way, that does not require the number $n$ of iteration to be integer.

However, the $n$th iteration of function $T$ can be written also in a way, that explicitly shows that it is also linear fraction;

(16) $~ ~ ~ \displaystyle T^n(z)=\frac{u_n+v_n z}{w_n+z}$

Evaluation through equation ( 03), (15), (05),(06), and comparison to (01) give the coefficients:

(17) $~ ~ ~ \displaystyle u_n=u$

(18) $~ ~ ~ \displaystyle v_n=$ $\displaystyle r \left(\frac{2^{n+1}}{2^n-\left(-\frac{-2 r (v+w)+2u+v^2+w^2}{u-v w}\right)^n}-1\right)+\frac{v-w}{2} $

(19) $~ ~ ~ \displaystyle w_n=$ $\displaystyle r \left(\frac{2^{n+1}}{2^n-\left(\frac{-2 r (v+w)+2u+v^2+w^2}{v w-u}\right)^n}-1\right)+\frac{-v+w}{2} = ~$ $\displaystyle v_n +w-v$

It looks strange, that $ u_n=u$, and does not depend on number $n$ of iteration. Consideration of expression

$\displaystyle \frac{u+v_n\frac{u+vz}{w+z}}{w_n+ \frac{u+vz}{w+z}}= \frac{u \frac{w+u_n}{v+w_n}+ \frac{u+v_n v}{v+w_n} z}{ \frac{u+w_n w}{v+w_n}+z}$

indicates, that, in order to keep $u_n=u$, the relation

$w+u_n=v+w_n$

should be satisfied; and, for experessions (18),(19) it, indeed, holds.

However, the revision of equations (16)-(19) with Mathematica also confirms their validity.

In such a way, the linear fraction can be iterated any number of times, the halfiteration and the complex iterations are straightforward. In Mathematica, this could be expressed with the built-in function Nest, but, up to year 2013, the software does not yet allow to use it for non-integer number of iterate; if the number of iterations cannot be expressed with some positive integer constant, Mathematica generates the error message instead of to evaluate the expression.

Fixed points

At real constants $u,v,w$, constant $r$ by (14) above determines, wether the transfer function $T$ by (01) above has real fixed points or not. The equation for fixed point $L$ can be writen as follows: $T(L)=L$. For the transfer function $T(z)=\frac{u+v z}{w+z}$, the equation becomes

$(20) ~ ~ ~ \displaystyle \frac{u+vL}{w+L}=L$

Equation (30) leads to the quadratic equation

$(21) ~ ~ ~ \displaystyle L^2+(w-v) L -u =0$

giving the solution $\displaystyle L=\frac{v-w}{2} \pm \sqrt{u+\left(\frac{v-w}{2}\right)^2}=\frac{v-w}{2} \pm r$

In other words, the transfer function has a real fixed point $L$, iff

$(22) ~ ~ ~ \displaystyle (w-v)^2/2 + u \ge 0$

In particular, it is satisfied at $u=0$, id est, in the case of transfer function by equaiton (02).

Superfunction

The nth iteration of function $f$ can be used to express the superfunction for the linear fraction; if $f$ is declared as transfer function, then, for some constant $t$, the superfunction $F$ can be written as follows

$(30) ~ ~ ~ F(z)=T^z(t)$

and the interse function $G=F^{-1}$ appears as the Abel function.

Linear fraction is one of transfer functions, for which the superfunction and the Abel function can be expressed in terms of elementary functions. For many cases, instead of to express the superfunction through the iterate of the transfer function, function, contrary, the iterate of the transfer function is expressed through the superfunction $F$ and the Abel function $G$ with

$(31) ~ ~ ~ T^n(z)=F(n+G(z))$

In order to get simple expression for superfunction, it has sense to simplify expressions (18) and (19), rewriting them as follows

$(32) ~ ~ ~ v_n = R_n + (v - w)/2$

$(33) ~ ~ ~ w_n = R_n - (v - w)/2$

where

$(34) ~ ~ ~ R_n= $ $\displaystyle \left(\frac{2}{ \displaystyle 1-\left(\frac{ u+(v^2+w^2)/2-(v+w) r}{v w-u}\right)^{\displaystyle n}}-1\right) r $

In this expression, the exponentiation of number $n$ of iteration appears only once.

For applications in physics, the case of real initial parameters u,v,w is of special interest. Derivative of the transfer function $T(z)=\frac{u+vz}{w+z}$ can be expressed as follows: $T'(z)=\frac{vw-u}{(w+z)^2}$

The non-integer iterate of the transfer function can be interpreted as real-holomorphic function only while $T'(z)>0$. id est, while $vw-u>0$. In addition, one should cary about singulatity at $z=-w$. Representaiton with equation (23) indicates, that also, for the real–holomorphic iterate, it is highly desirable to have positive parameter

$(35) ~ ~ ~ \displaystyle b= \frac{ u+(v^2+w^2)/2-(v+w) r}{v w-u} = \frac{\left( r- \frac{w+v}{2}\right)^2}{v w-u}$

Numerator in the formula above is transformed as follows:

$u+\frac{(v-w)^2}{4}-\frac{(v-w)^2}{4}+\frac{2v^2+2w^2}{4} - (v+w) r$ $= r^2 +\frac{-v^2-w^2+2 v w+ 2v^2+2w^2}{4} - (v+w) r$ $= r^2 +\frac{v^2+w^2+2 v w}{4} - (v+w) r$ $= (r - (v+w)/2)^2$

For $b>0$, the choice of the branch for the exponentiation $b^n$ at non–integer $n$ is straightforward, just choose the real value with $b^n=\exp(n \ln(b))$.

Using notation (24) $R_n$ can be expressed as follows:

$(36) ~ ~ ~ R_n=\displaystyle \left(\frac{2}{ \displaystyle 1-b^n}-1\right) r$

Then

$(37) ~ ~ ~ \displaystyle T^n(z)=\frac{u+v_n z}{w_n+z}$

$(38) ~ ~ ~ \displaystyle T^n(0)= \frac{u}{w_n}= \frac{u}{R_n - (v - w)/2} $

Tue superfunction for the transfer function $T$ can be written as follows:

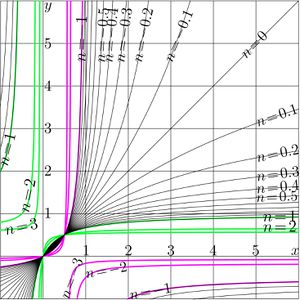
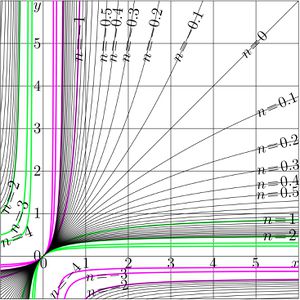
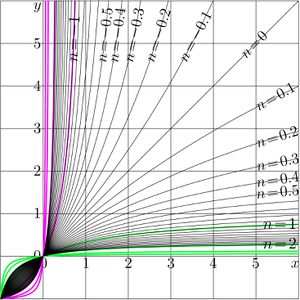
$(39) ~ ~ ~ \displaystyle F(z)=T^z(0)=$ \)\displaystyle \frac{u}{\displaystyle \left(\frac{2}{ \displaystyle 1-b^z}-1\right) r + \frac{w-v}{2} } $ The [[Abel function]] $G=F^{-1}$ can be obtained, inverting reresentation (38); the inversion is straightforward. =='"`UNIQ--h-6--QINU`"'Another special case== [[File:Frac1zt.jpg|360px|thumb| $y=T^n(x)~$ by (40) versus $x$ for various values of $n$]] The special case of the linear fraction cannot be represented in form (01). For example, consider the transfer function function $(40) ~ ~ ~ T(z)=-1/z$ and various functions that are [[linear conjugation]]s of (40) with $P\circ T\circ Q$. with linear functions $P$ and $Q=P^{-1{}$. On the first look, this case appears as very difficult because the formulas above cannot be applied as is. Hin this case, the [[superfunction]] can be expressed through the [[tan]] function, $(41) ~ ~ ~ \displaystyle F(z)=\tan\left( \frac{\pi}{2} z\right)$ then the Abel function $(42) ~ ~ ~ \displaystyle G(z)=\frac{2}{\pi} \arctan(z) $, and the iterate $(43) ~ ~ ~ \displaystyle T^n(z)=F(n+G(z)) \displaystyle = \tan\displaystyle\left( \frac{\pi}{2} \left( n + \frac{2}{\pi} \arctan(z) \right) \right)= \displaystyle \tan \left( \frac{\pi}{2} n + \arctan(z) \right)$ =='"`UNIQ--h-7--QINU`"'Case $T(z)=-a^2/z$== [[File:Frac2zt.jpg|360px|thumb| $y=T^n(x)~$ by (44) at $a=2$ versus $x$ for various $n$]] Case of transfer function (36) allows the straightforward generalization, $(44) ~ ~ ~ T(z)=-a^2/z$ In this case, the superfunction $(45)\displaystyle ~ ~ ~ F(z)= a \tan\left(\frac{\pi}{2} z\right)$ and the Abel function $(45)\displaystyle ~ ~ ~ G(z)=F^{-1}(z)= \frac{2}{\pi} \arctan\left(\frac{z}{a}\right)$ Then, the $n$th iteration of the [[transfer function]] $T$ by (44) can be expressed as follows: $(43)\displaystyle ~ ~ ~ T^{n}(z)= \frac{-a^2\, -a\, \cot\left(\frac{\pi}{2}\right)\, z}{-\, a\, \cot\left(\frac{\pi}{2}\right)\, +\, z}\( =='"`UNIQ--h-8--QINU`"'References== '"`UNIQ--references-00000000-QINU`"' http://www.ams.org/journals/bull/1993-29-02/S0273-0979-1993-00432-4/S0273-0979-1993-00432-4.pdf Walter Bergweiler. Iteration of meromorphic functions. Bull. Amer. Math. Soc. 29 (1993), 151-188. http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf D. Kouznetsov. Solution of F(x+1)=exp(F(x)) in complex z-plane. [[Mathematics of computation]] '''78''', (2009), 1647-1670 ' http://www.ils.uec.ac.jp.jp/~dima/PAPERS/2009vladie.pdf (English) http://mizugadro.mydns.jp/PAPERS/2010vladie.pdf (English) http://mizugadro.mydns.jp/PAPERS/2009vladir.pdf (Russian version) D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45. http://reference.wolfram.com/mathematica/ref/Nest.html Nest, Wolfram Mathematica 9 Documentation center, 2013. http://m.iopscience.iop.org/1751-8121/44/40/405205/pdf/1751-8121_44_40_405205.pdf http://arxiv.org/pdf/1105.3664.pdf Thomas Curtright, Xiang Jin and Cosmas Zachos. Approximate Solutions of Functional Equations. 2011 August 22. Journal of Physics A: Mathematical and Theoretical. 44 405205. doi:10.1088/1751-8113/44/40/405205 Received 21 May 2011, in final form 22 August 2011. Published 16 September 2011. © 2011 IOP Publishing Ltd http://web.abo.fi/fak/mnf/mate/kurser/dynsyst/Iteration%20of%20sin(x).pdf Kursernas Hemsidor. 273027 Introduction to Dynamical Systems 2012. Derivation of Niklas Carlsson;s formula. Cited by the state for December 2013: Let function f(x) be sin(x). We want to evaluate, approximately, the value of the nth iterate of f(x) ... If the formula is correct, it will take \)3\cdot10^{10}$ .. steps to reat 0.00001 from 1. .. $f^n \approx \sqrt{3/n}$.. How good is this formula? after 60000 iterations of the value 0.0071 and the discrepancy -4.7s-007 ..

Keywords

Abel function, Iteration, Linear fraction, Superfunction, Table of superfunctions, Tetration