Difference between revisions of "File:Logi2c4T1000.png"

Latest revision as of 14:06, 23 August 2025

Complex map of function LogisticSequence with critic value of parameter,

\[ u\!+\!\mathrm i v= \mathrm{LogisticSequence}_4(x\!+\!\mathrm i y) \]

This map appears as Fig.7.5 at page 75 of book «Superfunctions»^[1]^[2]
in order to show that the Holomorphic extension of the logistic sequence ^[3] is not chaotic.

The generators of the map are copypasted below

logiu

// The code below should be stored as logiu.cin

 DB LQ;
 DB QQ,Q2,Q3,Q4,Q5,Q6,Q7;
 DB C1,C2,C3,C4,C5,C6,C7;
 DB S1,S2,S3,S4,S5,S6,S7,S8;

 void maq(DB q){
 Q=q;
 QQ=Q*Q;
 Q2=QQ;
 Q3=QQ*Q;
 Q4=QQ*QQ;
 Q5=Q4*Q;
 Q6=Q3*Q3;
 Q7=Q6*Q;
 LQ=log(Q);
 C2=1.                                                           / (1.-Q) ;
 C3=2.                                                           /((1.-Q)*(1.-Q2) );
 C4=   (5.+Q)                                                    /((1.-Q)*(1.-Q2)*(1.-Q3) );
 C5=2.*(7.+Q*(3.+Q*2.))                                          /((1.-Q)*(1.-Q2)*(1.-Q3)*(1.-Q4) );
 C6=2.*(21.+Q*(14.+Q*(14.+Q*( 8.+Q*3.))))                        /((1.-Q)*(1.-Q2)*(1.-Q3)*(1.-Q4)*(1.-Q5));
 C7=4.*(33.+Q*(30.+Q*(37.+Q*(32.+Q*(27.+Q*(12.+Q*(8.+Q)))))))    /((1.-Q)*(1.-Q2)*(1.-Q3)*(1.-Q4)*(1.-Q5)*(1.-Q6));
 S1=1.;
 S2=1.                                                           / (Q-1.);
 S3=2.*Q                                                         /((Q-1.)*(Q2-1.));
 S4=   Q *(1.+5.*Q*Q)                                            /((Q-1.)*(Q2-1.)*(Q3-1.) );
 S5=2.*Q3*(3.+Q*(2.+QQ*7.))                                      /((Q-1.)*(Q2-1.)*(Q3-1.)*(Q4-1.) );
 S6=2.*Q3*(1.+Q*(3.+QQ*(14.+Q*(14.+Q*(7.+QQ*21)))))              /((Q-1.)*(Q2-1.)*(Q3-1.)*(Q4-1.)*(Q5-1.));
 S7=4.*Q4*(1.+Q*(5.+Q*(15.+Q*(12.+Q*(8.+Q*(30.+Q*(37.+Q*(27.+Q*(12.+QQ*(33.))))))))))
                                                                /((Q-1.)*(Q2-1.)*(Q3-1.)*(Q4-1.)*(Q5-1.)*(Q6-1.));
 S8=Q4*(1.+QQ*(5.+Q*(60.+Q*(69.+Q*(89.+Q*(162.+Q*(415.+Q*(495.+Q*(531.+Q*(267.+Q*(630.+Q*(705.+Q*(621.+Q*(396+Q*(165.+Q*429)
              )     )      )      )      )       )       )       )       )       )       )       )       )
        )                                                       /((Q-1.)*(Q2-1.)*(Q3-1.)*(Q4-1.)*(Q5-1.)*(Q6-1.)*(Q7-1.));
 ;
 printf("maq: Q=%9.6f\n",Q);}

 z_type J(z_type z){ return .5-sqrt(.25-z/Q); }
 z_type H(z_type z){ return Q*z*(1.-z); }
 z_type f(z_type z){z_type e;e=exp(LQ*z);return e*(1.+e*(C2+e*(C3+e*(C4+e*(C5+e*(C6+e*C7))))));  }
 z_type F(z_type z){     if(Re(z)>-6.) return H(F(z-1.));   return f(z);}
 z_type e(z_type z){                     return z*(1.+z*(S2+z*(S3+z*(S4+z*(S5+z*(S6+z*(S7+z* S8)))))));}
 z_type E(z_type z){     if(abs(z)>.1) return  E(J(z))+1.;
                         return log(e(z))/LQ;} 
 //#include "efjh.cin"
 z_type u(z_type z){
 DB q1 =Q-1.;
 DB q2 =Q-2.;
 DB q3 =Q-3.;
 DB q2L=log(q2);
 DB U0=q1/Q;
 DB U1=1.;
 DB U2=-Q/(q1*q2);
 DB U3=-2.*QQ/(q1*q1*q2*q2*q3);
 DB U4=-2.*Q3*(Q-7.)/(q1*q1*q1*q2*q2*q2*(-21.+Q*(22.+Q*(-8.+Q))) );
 z_type e=-exp(z*q2L)*cos(M_PI*z);
 //return U0+e;
 //return U0+e*(1.+e*(U2)); 
 //return U0+e*(U1+e*(U2+e*U3)); 
 return U0+e*(U1+e*(U2+e*(U3+e*U4))); 
 }

 z_type U(z_type z){     if(Re(z)+3*fabs(Im(z))>-6.) return H(U(z-1.));   return u(z);}

// Let me know if any problem with use of the routine "U".
//

C++ generator of curves

// Routine logiu.cin above and files ado.cin and conto.cin should be loaded to the working directory in order to compile the code below

 #include <math.h>
 #include <stdio.h>
 #include <stdlib.h>
 #define DB double
 #define DO(x,y) for(x=0;x<y;x++)
 using namespace std;
 #include <complex>
 typedef complex<double> z_type;
 #define Re(x) x.real()
 #define Im(x) x.imag()
 #define I z_type(0.,1.)
 #include "conto.cin"
 #include "efjh.cin"
 main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
  int M=408,M1=M+1;
  int N=602,N1=N+1;
 DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
 char v[M1*N1]; // v is working array
 FILE *o;o=fopen("logi2c4a.eps","w");ado(o,126,124);
 fprintf(o,"62 62 translate\n 20 20 scale\n");
 DO(m,M1) X[m]=-3.01+.015*(m-.5);
 DO(n,300) Y[n]=-3.+.01*n;
          Y[300]=-0.002;
          Y[301]= 0.002;
 for(n=302;n<N1;n++) Y[n]=-3.+.01*(n-1);
 fprintf(o,"1 setlinejoin 2 setlinecap\n");  //p=.8;q=.4;
 for(m=-3;m<4;m++){if(m==0){M(m,-3.04)L(m,3.04)} else{M(m,-3)L(m,3)}}
 for(n=-3;n<4;n++){        M(  -3  ,n)L(3,n)}
 fprintf(o,".008 W 0 0 0 RGB S\n");
 maq(4.);
 DO(m,M1)DO(n,N1){g[m*N1+n]=9999; f[m*N1+n]=9999;}
 DO(m,M1){x=X[m]; //printf("%5.2f\n",x);
 DO(n,N1){y=Y[n]; z=z_type(x,y);        
   c=F(z);
   p=Re(c);q=Im(c);     
   if(p>-49 && p<49)    {g[m*N1+n]=p;}
   if(q>-49 && q<49)    {f[m*N1+n]=q;}
       }}
 fprintf(o,"1 setlinejoin 1 setlinecap\n");  //p=.8;q=.4;
 p=2.;q=.5;
 //#include"plof.cin"
 for(m=-2;m<2;m++) 
 for(n=1;n<10;n+=1)conto(o,f,w,v,X,Y,M,N, (m+.1*n),-q, q);fprintf(o,".005 W 0 .6 0 RGB S\n");
 for(m=0;m<2;m++) 
 for(n=1;n<10;n+=1)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q, q);fprintf(o,".005 W .9 0 0 RGB S\n");
 for(m=0;m<2;m++) 
 for(n=1;n<10;n+=1)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q, q);fprintf(o,".005 W 0 0 .9 RGB S\n");
 for(m= 1;m<5;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p);   fprintf(o,".02 W .9 0 0 RGB S\n");
 for(m= 1;m<5;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p);   fprintf(o,".02 W 0 0 .9 RGB S\n");
 for(m=-4;m<5;m++) conto(o,g,w,v,X,Y,M,N, (0.+m),-p,p);   fprintf(o,".02 W 0 0 0 RGB S\n");
                  conto(o,f,w,v,X,Y,M,N, (0.  ),-p,p);   fprintf(o,".02 W .6 0 .6 RGB S\n");
 fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
 system("epstopdf logi2c4a.eps"); // for linux
 system(    "open logi2c4a.pdf"); // for mac
 getchar(); system("killall Preview");
 }
//

// Copileft 2009, 2012 by Dmitrii Kouznetsov

Latex generator of labels

% File logi2c4T.pdf should be generated with the code above in order to compile the Latex document below

%

\documentclass[12pt]{article} %<br>
\usepackage{geometry} %<br>
\usepackage{graphics} %<br>
\usepackage{rotating} %<br>
\paperwidth 128pt %<br>
\paperheight 127pt %<br>
\topmargin -104pt %<br>
\oddsidemargin -90pt %<br>
\newcommand \sx {\scalebox} %<br>
\newcommand \ing \includegraphics %<br>
\newcommand \rot {\begin{rotate}} %<br>
\newcommand \ero {\end{rotate}} %<br>
\begin{document} %<br>
\newcommand \axes { %<br>
\put(  2,124){\sx{.5}{$y$}} %<br>
\put(  2,105){\sx{.5}{$2$}} %<br>
\put(  2,85){\sx{.5}{$1$}} %<br>
\put(  2, 65){\sx{.5}{$0$}} %<br>
\put(-.8, 45){\sx{.5}{$-\!1$}} %<br>
\put(-.8, 25){\sx{.5}{$-\!2$}} %<br>
\put( 22,  1){\sx{.5}{$-2$}} %<br>
\put( 42,  1){\sx{.5}{$-\!1$}} %<br>
\put( 65,  1){\sx{.5}{$0$}} %<br>
\put( 85,  1){\sx{.5}{$1$}} %<br>
\put(105,  1){\sx{.5}{$2$}} %<br>
\put(124.6,  1){\sx{.5}{$x$}} %<br>
} %<br>
\begin{picture}(122,122)  \put( 4, 4){\ing{logi2c4a}} %<br>
\put(7,110){\rot{ 0.}\sx{.6}{$v\!=\!0$}\ero} %<br>
\put(7, 87.4){\rot{ 0.}\sx{.6}{$u\!=\!0$}\ero} %<br>
\put(7, 64.5){\rot{ 0.}\sx{.6}{$v\!=\!0$}\ero} %<br>
\put(7, 41.6){\rot{ 0.}\sx{.6}{$u\!=\!0$}\ero} %<br>
\put(7,  19){\rot{ 0.}\sx{.6}{$v\!=\!0$}\ero} %<br>
\put(34,70){\rot{50}\sx{.5}{$u\!=\!0.1$}\ero} %<br>
\put(44,68){\rot{58}\sx{.5}{$u\!=\!0.2$}\ero} %<br>
\put(56,68){\sx{.5}{$v\!=\!0.1$}} %<br>
\put(53,61){\sx{.5}{$v\!=\!-0.1$}} %<br>
\axes  %<br>
\end{picture} %<br>
\end{document} %<br>
%

References

↑ https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics - 2020/7/28
↑ https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.
↑ https://link.springer.com/article/10.3103/S0027134910020049
http://mizugadro.mydns.jp/PAPERS/2010logistie.pdf D.Kouznetsov. Holomorphic extension of the logistic sequence. Moscow University Physics Bulletin, 2010, No.2, p.91-98. (Russian version: p.24-31)

Keywords

«Holomorphic extension of the Logistic sequence», «LogisitcOperator», «LogisticSequence», «Table of superfunctions», «Transfer equation», «Superfunction», «Superfunctions»,

File history

Click on a date/time to view the file as it appeared at that time.

	Date/Time	Thumbnail	Dimensions	User	Comment
current	17:50, 20 June 2013		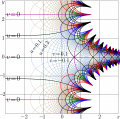1,772 × 1,758 (1.39 MB)	Maintenance script (talk \| contribs)	Importing image file

You cannot overwrite this file.

File usage

The following page uses this file:

LogisticSequence

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Horizontal resolution	393.7 dpc
Vertical resolution	393.7 dpc

[1] ttps://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics - 2020/7/28

[2] ttps://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.

[3] ttps://link.springer.com/article/10.3103/S0027134910020049
http://mizugadro.mydns.jp/PAPERS/2010logistie.pdf D.Kouznetsov. Holomorphic extension of the logistic sequence. Moscow University Physics Bulletin, 2010, No.2, p.91-98. (Russian version: p.24-31)

[1]

[2]

[3]

@@ Line 1: / Line 1: @@
+{{oq|Logi2c4T1000.png|Original file ‎(1,772 × 1,758 pixels, file size: 1.39 MB, MIME type: image/png)}}
 [[Complex map]] of function [[LogisticSequence]] with critic value of parameter,
-: $ u\!+\!\mathrm i v= \mathrm{LogisticSequence}_4(x\!+\!\mathrm i y)$
+\[
+u\!+\!\mathrm i v= \mathrm{LogisticSequence}_4(x\!+\!\mathrm i y)
+\]
+This map appears as Fig.7.5 at page 75 of book
+«[[Superfunctions]]»<ref>
+https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. [[Superfunctions]]: Non-integer iterates of holomorphic functions. [[Tetration]] and other [[superfunction]]s. Formulas,algorithms,tables,graphics - 2020/7/28
+</ref><ref>https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). [[Superfunctions]]: Non-integer iterates of holomorphic functions. [[Tetration]] and other [[superfunction]]s. Formulas, algorithms, tables, graphics. Publisher: [[Lambert Academic Publishing]].
+</ref>
+<br>
+in order to show that the [[Holomorphic extension of the logistic sequence]]
+<ref>
+https://link.springer.com/article/10.3103/S0027134910020049 <br>
+http://mizugadro.mydns.jp/PAPERS/2010logistie.pdf
+D.Kouznetsov. [[Holomorphic extension of the logistic sequence]]. [[Moscow University Physics Bulletin]], 2010, No.2, p.91-98. (Russian version: p.24-31)
+</ref>
+is not chaotic.
 The generators of the map are copypasted below
 ==logiu==
 // The code below should be stored as [[logiu.cin]]
+<pre>
  DB LQ;
  DB QQ,Q2,Q3,Q4,Q5,Q6,Q7;
@@ Line 69: / Line 88: @@
 // Let me know if any problem with use of the routine "U".
+//</pre>
 ==C++ generator of curves==
 // Routine [[logiu.cin]] above and files [[ado.cin]] and [[conto.cin]] should be loaded to the working directory in order to compile the code below
+<pre>
  #include <math.h>
  #include <stdio.h>
@@ Line 129: / Line 148: @@
  getchar(); system("killall Preview");
  }
+//</pre>
 // Copileft 2009, 2012 by Dmitrii Kouznetsov
 ==Latex generator of labels==
 % File [[logi2c4T.pdf]] should be generated with the code above in order to compile the [[Latex]] document below
+%<pre>
-%<nowiki> %<br>
 \documentclass[12pt]{article} %<br>
 \usepackage{geometry} %<br>
@@ Line 175: / Line 193: @@
 \end{picture} %<br>
 \end{document} %<br>
+%</pre>
-%</nowiki>
 ==References==
+{{ref}}
-<references/>
+{{fer}}
+==Keywords==
-http://tori.ils.uec.ac.jp/PAPERS/2010logistie.pdf D.Kouznetsov. Holomorphic extension of the logistic sequence. [[Moscow University Physics Bulletin]], 2010, No.2, p.91-98. (Russian version: p.24-31)
+«[[Holomorphic extension of the Logistic sequence]]»,
+«[[LogisitcOperator]]»,
+<b>«[[LogisticSequence]]»</b>,
+«[[Table of superfunctions]]»,
+«[[Transfer equation]]»,
+«[[Superfunction]]»,
+«[[Superfunctions]]»,
+[[Category:Book]]
+[[Category:BookMap]]
+[[Category:C++]]
 [[Category:Complex map]]
-[[Category:LogisticSequence]]
+[[Category:Elutin Pavel Vyacheslavovich]]
+[[Category:Latex]]
+[[Category:Logistic operator]]
+[[Category:Logistic sequence]]
 [[Category:Superfunction]]
+[[Category:Superfunctions]]