Difference between revisions of "File:AuPow2Plot.jpg"
(Importing image file) |
($ -> \() |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | {{oq|AuPow2Plot.jpg|Original file (1,577 × 1,469 pixels, file size: 219 KB, MIME type: image/jpeg)}} |
||
| − | Importing image file |
||
| + | |||
| + | Explicit plof of two [[abelpower]] functions: |
||
| + | |||
| + | \(y\!=\)[[AuPow]]\(_2(x)\!=\! \log_2\!\big(\ln(x)\big)~\), blue curve |
||
| + | |||
| + | and |
||
| + | |||
| + | \(y\!=\)[[AdPow]]\(_2(x)\!=\! \log_2\!\big(\ln(1/x)\big)~\), red curve |
||
| + | |||
| + | ==[[C++]] generator of curves== |
||
| + | //File [[ado.cin]] should be loaded in order to compile the code below. |
||
| + | <pre> |
||
| + | #include<math.h> |
||
| + | #include<stdio.h> |
||
| + | #include<stdlib.h> |
||
| + | #define DB double |
||
| + | #define DO(x,y) for(x=0;x<y;x++) |
||
| + | //#using namespace std; |
||
| + | //#include <complex> |
||
| + | //typedef std::complex<double> z_type; |
||
| + | #define Re(x) x.real() |
||
| + | #define Im(x) x.imag() |
||
| + | #define I z_type(0.,1.) |
||
| + | #include "ado.cin" |
||
| + | |||
| + | DB B=2.; |
||
| + | DB F(DB z) { return exp( exp( log(B)*z));} |
||
| + | DB G(DB z) { return log( log(z) )/log(B);} |
||
| + | DB H(DB z) { return log( log(1./z))/log(B);} |
||
| + | |||
| + | DB T(DB z) { return exp(B*log(z));} |
||
| + | DB U(DB z) { return exp(log(z)/B);} |
||
| + | |||
| + | int main(){ int m,n; double x,y,t; FILE *o; |
||
| + | o=fopen("aupow2plo.eps","w"); ado(o,720,740); |
||
| + | fprintf(o,"10 510 translate 100 100 scale\n"); |
||
| + | #define M(x,y) fprintf(o,"%6.3f %6.3f M\n",0.+x,0.+y); |
||
| + | #define L(x,y) fprintf(o,"%6.3f %6.3f L\n",0.+x,0.+y); |
||
| + | |||
| + | fprintf(o,"2 setlinecap 1 setlinejoin .03 W 0 0 1 RGB S\n"); |
||
| + | |||
| + | for(m=0;m<8;m++) {M(m,-5)L(m,2)} |
||
| + | for(n=-5;n<3;n++) {M(0,n)L(7,n)} |
||
| + | fprintf(o,".01 W 0 0 0 RGB S\n"); |
||
| + | |||
| + | DO(m,98){x=.01+.01*m; y=H(x); if(m==0)M(x,y) else L(x,y);} fprintf(o,".04 W 1 0 0 RGB S\n"); |
||
| + | |||
| + | DO(m,601){x=1.03+.01*m; y=G(x); if(m==0)M(x,y) else L(x,y);} fprintf(o,".04 W 0 0 1 RGB S\n"); |
||
| + | |||
| + | fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o); |
||
| + | system("epstopdf aupow2plo.eps"); |
||
| + | system( "open aupow2plo.pdf"); |
||
| + | getchar(); system("killall Preview"); |
||
| + | } |
||
| + | </pre> |
||
| + | |||
| + | ==[[Latex]] generator of labels== |
||
| + | % File aupow2plo.eps should be generated with the code above in order to Latex the document below. |
||
| + | <pre> |
||
| + | \documentclass[12pt]{article} |
||
| + | \usepackage{geometry} |
||
| + | \usepackage{graphicx} |
||
| + | \usepackage{rotating} |
||
| + | \paperwidth 760pt |
||
| + | \paperheight 708pt |
||
| + | \topmargin -94pt |
||
| + | \oddsidemargin -81pt |
||
| + | \textwidth 1100pt |
||
| + | \textheight 1100pt |
||
| + | \pagestyle {empty} |
||
| + | \newcommand \sx {\scalebox} |
||
| + | \newcommand \rot {\begin{rotate}} |
||
| + | \newcommand \ero {\end{rotate}} |
||
| + | \newcommand \ing {\includegraphics} |
||
| + | \parindent 0pt |
||
| + | \pagestyle{empty} |
||
| + | \begin{document} |
||
| + | \begin{picture}(742,702) |
||
| + | %\put(51,1){\ing{01plo}} |
||
| + | \put(51,1){\ing{aupow2plo}} |
||
| + | \put(24,696){\sx{4}{$y$}} |
||
| + | \put(24,598){\sx{4}{$1$}} |
||
| + | \put(24,498){\sx{4}{$0$}} |
||
| + | \put(-4,398){\sx{4}{$-1$}} |
||
| + | \put(-4,298){\sx{4}{$-2$}} |
||
| + | |||
| + | \put(-4,198){\sx{4}{$-3$}} |
||
| + | \put(-4,098){\sx{4}{$-4$}} |
||
| + | \put(150,476){\sx{4}{$1$}} |
||
| + | \put(250,476){\sx{4}{$2$}} |
||
| + | \put(351,476){\sx{4}{$3$}} |
||
| + | \put(451,476){\sx{4}{$4$}} |
||
| + | \put(552,476){\sx{4}{$5$}} |
||
| + | \put(652,476){\sx{4}{$6$}} |
||
| + | \put(738,476){\sx{4}{$x$}} |
||
| + | \put(366,546){\sx{3.7}{\rot{13}$y\!=\!\mathrm{AuPow}_2(x)$\ero}} |
||
| + | %\put(242,66){\sx{3.8}{\rot{82}$y\!=\!\mathrm{AuPow}_2(x)$\ero}} |
||
| + | \put(80,666){\sx{3.7}{\rot{-77}$y\!=\!\mathrm{AdPow}_2(x)$\ero}} |
||
| + | \end{picture} |
||
| + | \end{document} |
||
| + | </pre> |
||
| + | |||
| + | ==References== |
||
| + | {{ref}} |
||
| + | |||
| + | https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. [[Superfunctions]]: Non-integer iterates of holomorphic functions. [[Tetration]] and other superfunctions. Formulas,algorithms,tables,graphics ペーパーバック – 2020/7/28 |
||
| + | |||
| + | https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). [[Superfunctions]]: Non-integer iterates of holomorphic functions. [[Tetration]] and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: [[Lambert Academic Publishing]]. |
||
| + | |||
| + | {{fer}} |
||
| + | |||
| + | ==Keywords== |
||
| + | «[[Abel function]]», |
||
| + | <b>«[[]]»<b>, |
||
| + | <b>«[[Abelpower]]»</b>, |
||
| + | <b>«[[AdPow]]»</b>, |
||
| + | <b>«[[AuPow]]»</b>, |
||
| + | «[[Superpower]]», |
||
| + | «[[Superfunctions]]», |
||
| + | «[[Table of superfunctions]]», |
||
| + | |||
| + | [[Category:Abel function]] |
||
| + | [[Category:Abelpower]] |
||
| + | [[Category:AdPow]] |
||
| + | [[Category:AuPow]] |
||
| + | [[Category:Book]] |
||
| + | [[Category:BookPlot]] |
||
| + | [[Category:Explicit plot]] |
||
| + | [[Category:Power function]] |
||
| + | [[Category:Superfunction]] |
||
| + | [[Category:Superfunctions]] |
||
Latest revision as of 14:03, 16 August 2025
Explicit plof of two abelpower functions:
\(y\!=\)AuPow\(_2(x)\!=\! \log_2\!\big(\ln(x)\big)~\), blue curve
and
\(y\!=\)AdPow\(_2(x)\!=\! \log_2\!\big(\ln(1/x)\big)~\), red curve
C++ generator of curves
//File ado.cin should be loaded in order to compile the code below.
#include<math.h>
#include<stdio.h>
#include<stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
//#using namespace std;
//#include <complex>
//typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "ado.cin"
DB B=2.;
DB F(DB z) { return exp( exp( log(B)*z));}
DB G(DB z) { return log( log(z) )/log(B);}
DB H(DB z) { return log( log(1./z))/log(B);}
DB T(DB z) { return exp(B*log(z));}
DB U(DB z) { return exp(log(z)/B);}
int main(){ int m,n; double x,y,t; FILE *o;
o=fopen("aupow2plo.eps","w"); ado(o,720,740);
fprintf(o,"10 510 translate 100 100 scale\n");
#define M(x,y) fprintf(o,"%6.3f %6.3f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%6.3f %6.3f L\n",0.+x,0.+y);
fprintf(o,"2 setlinecap 1 setlinejoin .03 W 0 0 1 RGB S\n");
for(m=0;m<8;m++) {M(m,-5)L(m,2)}
for(n=-5;n<3;n++) {M(0,n)L(7,n)}
fprintf(o,".01 W 0 0 0 RGB S\n");
DO(m,98){x=.01+.01*m; y=H(x); if(m==0)M(x,y) else L(x,y);} fprintf(o,".04 W 1 0 0 RGB S\n");
DO(m,601){x=1.03+.01*m; y=G(x); if(m==0)M(x,y) else L(x,y);} fprintf(o,".04 W 0 0 1 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf aupow2plo.eps");
system( "open aupow2plo.pdf");
getchar(); system("killall Preview");
}
Latex generator of labels
% File aupow2plo.eps should be generated with the code above in order to Latex the document below.
\documentclass[12pt]{article}
\usepackage{geometry}
\usepackage{graphicx}
\usepackage{rotating}
\paperwidth 760pt
\paperheight 708pt
\topmargin -94pt
\oddsidemargin -81pt
\textwidth 1100pt
\textheight 1100pt
\pagestyle {empty}
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \ing {\includegraphics}
\parindent 0pt
\pagestyle{empty}
\begin{document}
\begin{picture}(742,702)
%\put(51,1){\ing{01plo}}
\put(51,1){\ing{aupow2plo}}
\put(24,696){\sx{4}{$y$}}
\put(24,598){\sx{4}{$1$}}
\put(24,498){\sx{4}{$0$}}
\put(-4,398){\sx{4}{$-1$}}
\put(-4,298){\sx{4}{$-2$}}
\put(-4,198){\sx{4}{$-3$}}
\put(-4,098){\sx{4}{$-4$}}
\put(150,476){\sx{4}{$1$}}
\put(250,476){\sx{4}{$2$}}
\put(351,476){\sx{4}{$3$}}
\put(451,476){\sx{4}{$4$}}
\put(552,476){\sx{4}{$5$}}
\put(652,476){\sx{4}{$6$}}
\put(738,476){\sx{4}{$x$}}
\put(366,546){\sx{3.7}{\rot{13}$y\!=\!\mathrm{AuPow}_2(x)$\ero}}
%\put(242,66){\sx{3.8}{\rot{82}$y\!=\!\mathrm{AuPow}_2(x)$\ero}}
\put(80,666){\sx{3.7}{\rot{-77}$y\!=\!\mathrm{AdPow}_2(x)$\ero}}
\end{picture}
\end{document}
References
https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics ペーパーバック – 2020/7/28
https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.
Keywords
«Abel function», «[[]]», «Abelpower», «AdPow», «AuPow», «Superpower», «Superfunctions», «Table of superfunctions»,
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 06:10, 1 December 2018 | 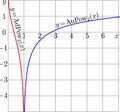 | 1,577 × 1,469 (219 KB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.