Difference between revisions of "Asymptotic"

From TORI
Jump to navigation Jump to search
m
(add picture)
 
(10 intermediate revisions by the same user not shown)
Line 2: Line 2:
 
Warning: this article is under construction.
  
Warning: this article is under construction.
   
−
[[Asymptotic]] is statement about behaviors of a function (usually a [[holomorphic function]]) in some vicinity of some its singularity or at large values of the argument.
 +
[[Asymptotic]] \(A\) of function \(f\) at point \(z_0\) on the domain \(D\in\mathbb C\)
  +
is special kind of approximation, characterized in that, that its quality improves
  +
while the input of function, remaining within domain \(D\) approaches \(z_0\).
  +
Here, \(z_0\) is either a [[comlex number]] or \(\infty\).
   
  +
[[Asymptotic]]s are qualified
−
The main application of [[Asymptotic]] is approximation of the function, replacement of a function to another function, that is easier to evaluate, for those ranges of values of the argument, where the function and its [[asymptotic]] have similar properties (and similar values).
  
  +
by the criteria of the "quality" of the approximation,
  +
by the kind of the limiting point \(z_0\)
  +
and by the shape of domain \(D\).
   
−
[[Asymptotic]] of a function \(f\) at a point \(C\) is a function \(A\) such that
 +
Usually, [[asympototic]] \(A\) is easier to evaluate than approximated function \(f\).
  +
  +
Sometimes, for some applications, the properties of [[asumptotic]] coincide with those of the approximated function. In these cases, following the last 6th of the [[TORI asioms]], the concept that uses asymtotic, has priority.
  +
  +
[[Asymototic]]s can be used for fast, qualitative estimates, but also for the precise evaluation of the approximated function.
  +
  +
==Apology==
  +
  +
There are several various definitions of term «[[Asymtotic]]» at various sites, t various dictionaries. Often, term «[[Asymtotic]]» is used in an [[euistic]] mode,
  +
assuming, that «Everybody nows» and with hope, that the professional pure mathematicians understand the problem and redo it with mathematical rugosity.
  +
<br>
  +
Often, sigh a hope is not supported with interest and pacience of so-called «pure mathematicians; one example of such a case is resented in the fairy tale «[[Lesson of quantum topology]]».<br>
  +
According to legend, the [[Greatest genius of all centuries and all civilizations]] gunsek [[Mao Zedong]] used to say, that one may count only with own eforts <ref>
  +
https://www.marxists.org/reference/archive/mao/works/red-book/ch21.htm
  +
Quotations from [[Mao Tse Tung]]
  +
21. Self-Reliance and Arduous Struggle
  +
«On what basis should our policy rest? It should rest on our own strength, and that means regeneration through one's own efforts. ..»
  +
</ref>. At the testing of Chinese [[nuclear weapon]], the people were not even alerted. Even worse, it was assumed, that at the use, the significant part of population of China will be dead, and the gensek still will have sufficient number of slaves to maintain his luxury style of life. No any opposition of this idea had been allowed in 1964's China: every citizen could count only whit his own efforts.<ref>
  +
https://www.upi.com/Archives/1964/10/17/Maos-theory-on-atomic-bomb-They-cant-kill-us-all/1653831424805/
  +
UPI ARCHIVES OCTOBER 17, 1964//
  +
Mao's theory on atomic bomb: They can't kill us all.
  +
TOKYO, Oct. 17, 1964 (UPI) -- Chairman [[Mao Tse-Tung]] maintains that Communist China has nothing to fear from nuclear weapons. But his people have paid a fearful price to develop the atomic bomb of their own. Mao is said to have told a Yugoslav visitor to Peking in 1957, "We have a very large territory and a big population. Atomic bombs could not kill all of us." //
  +
"What if they killed 300 million of us? We would still have many people left."
  +
</ref>.
  +
  +
Following the Ideas of the [[Greatest genius of all centuries and all civilizations]],
  +
this article suggests definition of term [[Asymptoric]] in the next section.
  +
  +
==Definition==
  +
  +
Assume function \(f\) is defined at some domain \(B \in \mathbb C\)
  +
  +
Assume, some point \(z_0\) is specified; it can be a comely number or infinity.
  +
  +
Assume some domain \(D\in B\) is specified.
  +
  +
Assume some [[special function]] \(A\) is defined at \(D\).
  +
  +
Assume some holomorphic function \(\tau\) is defined a the set of values of function
  +
\(f\).
  +
  +
Let
  +
\[
  +
\lim_{z\to z_0, \ z\in D} \Big(
  +
\tau\big(f(z)\big) - \tau\big(A(z)\big) \Big) =0
  +
\]
  +
  +
Then, function \(A\) is
  +
[[asymtoric]] of function \(f\)
  +
at domain \(D\)
  +
with the [[criterion function]] \(\tau\).
  +
  +
The same can be written as follows:
 
\[
  
\[
  +
f(z) \underset{\mathrm{\tau, \ z\in D,\ z\to z_0}}{\sim} A(z)
−
\lim_{z\to C}\ (f(z)-A(z))\,B(z)=0,
  
 
\]
  
\]
−
where \( |B(z)|\to\infty \) as \( z\to C \).
  
   
  +
If function \(\tau\) is not specified, by default, it is assumed to be [[identity function]].
−
Here \(C\) may be a complex number or \( \infty \).
  
  +
  +
Function \(\ R(z)=f(z)\!-\!A(z) \ \) is called [[Residual]] of asymtotic \(A\) of function \(f\)
  +
  +
Function
  +
\[\ a(z)=-\lg\left(\frac
  +
{|f(z)\!-\!A(z)|}
  +
{|f(z)|\!+\!|A(z)|}
  +
\right)
  +
\]
  +
  +
is called [[agreement]] of asymptotic \(A\) with function \(f\).
  +
  +
The agreement gives the criterion of quality of the asymptotic \(A\) at the use as the [[primary approximation]]
  +
for the [[numerical implementation]] of function \(f\).
  +
  +
For the approximation of a function, it is desirable that residual approach zero,
  +
and the agreement remain big, say, comparable to the amount of decimal digits that are supported in arithmetic used in the numerical implementation. The most of [[numerical implementation]]s loaded at TORI provide of order of 14 significant figures.
  +
  +
For some asymptotics, it is not possible to achieve \(R\to 0\).
  +
  +
Then, as criterion, the "small residual"
  +
\[
  +
r(z)=\tau(f(z))\!-\!\tau(A(z))
  +
\]
  +
can be used; function
  +
\[
  +
\alpha (z)= -\lg\left(\frac
  +
{|\tau(f(z)) - \tau(A(z))|}
  +
{|\tau(f(z))|+ |\tau(A(z))|}
  +
\right)
  +
\]
  +
can be used instead of the [[agreement]];
  +
it is desirable to provide small values of \(|r(z)|\)
  +
and keep big values of \(\alpha(z)\) at least for \(z\) in vicinity of \(z_0\).
  +
  +
==Notes about the definition above==
  +
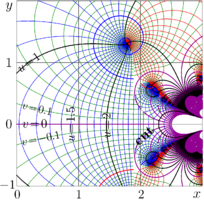
<div class="thumb tright" style="float:right; margin:-44px 0px 2px 8px; width:308px; background-color:#fff">
  +
&nbsp; {{pic|Fig1802.jpg|300px}}<small><center>\(u\!+\!\mathrm i v\!=\!\mathrm{Filog}(x\!+\mathrm i y)\), bottom of Fig.18.2<!-- at page 248 !--><br> in book «[[Superfunctions]]»<ref>
  +
https://www.morebooks.de/shop-ui/shop/product/978-620-2-67286-3
  +
[Superfunctions]]. [[Lambet Academic Publishing]], 2020.
  +
</ref><ref>
  +
https://mizugadro.mydns.jp/BOOK/468.pdf D.Kouznetsov. [[Superfunctions]]. 2015-2020.
  +
</ref></center></small>
  +
</div>
  +
  +
Function \(A\) is supposed to be already known and well described.
  +
There is no sense to approximate some unknown function with anther unknown function.
  +
Ideally, asymtorotic \(A\) is [[elementary function]], but, generally, it can be any [[Special function]].
  +
  +
In actions, talking about asumtotics, often one does not specify the domain \(D\),
  +
assuming, that it is obvious.
  +
Usually, it is imlicitly assumed, that
  +
\(\tau\) is either [[identity function]]
  +
or natural [[logarithm]].
  +
  +
In general, some function may have several asymtoirics with different domains \(D\) -
  +
especially is \(z_0=\infty\) or \(z_0\) belongs to the branch cut of function \(f\).
  +
  +
One example of such a function is [[Filog]]; its [[complex map]] is shown in figure at right.<br>
  +
[[Filog]]\((\beta)\)
  +
expresses the [[fixed point]] of [[logarithm]] to base \(b=\mathrm e^\beta\) that is
   
  +
\(\log_b = (z \!\mapsto\! \log(\beta z))\).
−
In many cases, additional restrictions on the values of \(z\) are imposed in this limit; these restrictions define the [[domain of validity]] of the [[asymptotic]].
  
   
  +
At real \(z_0 < \exp(1/\mathrm d)\), the asymptotic of function [[Filog]] depends on the way he input approaches this value. <!--, and various [[SuperExponential]]s can be constructed with this fixed points;!-->
−
Function \(B\) qualifies, characterizes the precision of the asymptotic.
  
   
  +
If we extend the definition of asymptotic and allow the asymptotic to be a function of two arguments, then the [[tetration]] to base \(b=\exp(1/\mathrm e)\) can be considered as
−
Often, \(B(z)\) is expressed as some power of \(z-C\) or
  
  +
[[asymptotic]] of tetration to base \(b=\exp(\beta)\) while real part of \(\beta\) remains bigger than \(1/\mathrm e\); [[tetration]] being considered as function of logarithm of the base is not holomorphic at this point.
−
(if \(C\) is zero or \(\infty\)) just some [[power function]] of \(z\).
  
   
−
Combinations of \(z\) with \(\log(z) \) or with \(\log(z-C) \) also can be used as \(B(z)\).
  
   
 
==Conditional limit==
  
==Conditional limit==
   
−
Some restrictions can be applied to values of \(z\) that are allowed in the limit above.
 +
Some restrictios can be applied to values of \(z\) that are allowed in the limit above.
   
 
If the imaginary part of \(z\) is assumed to remain in the interval \(a,b\),
  
If the imaginary part of \(z\) is assumed to remain in the interval \(a,b\),
−
then, the [[asymptotic]] \(A\) is qualified as [[strip asymptotic]].
 +
then, the asymptotic \(A\) is qualified as [[strip asymptotic]].
  +
  +
"Fast" growth of \(B\) at \(C\) means that the asymptotic \(A\) is "good", robust, and is useful for the numeric implementation of function \(f\).
   
 
Two special cases of restrictions on values of \(z\) in the limit above are considered in the two subsections below.
  
Two special cases of restrictions on values of \(z\) in the limit above are considered in the two subsections below.
Line 40: Line 159:
 
\(\Re(z) \to +\infty\).
  
\(\Re(z) \to +\infty\).
   
−
Then the [[asymptotic]] \(A\) is qualified as [[Strip asymptotic]].
 +
Then the asympotic \(A\) is qualified as [[Strip asymptotic]].
   
 
===[[Sectorial asymptotic]]===
  
===[[Sectorial asymptotic]]===
   
−
The restriction may refer to the phase of the [[complex number]] \(z\);
 +
The restriction may refer to the phase of the compass number \(z\);
−
it allowed to have values from some sector at the complex plane:
 +
it allowed to have values fro some sector at the complex plane:
   
 
\( z = r \ \exp(\mathrm i t) \)
  
\( z = r \ \exp(\mathrm i t) \)
Line 53: Line 172:
 
(t_{\mathrm{min}},t_{\mathrm{max}})\)
  
(t_{\mathrm{min}},t_{\mathrm{max}})\)
   
−
Then, the asymtotic \(A\) is qualified as [[Sectorial asymptotic]].
 +
Then, the asymtiric \(A\) is qualified as [[Sectorial asymptotic]].
   
−
For finite number \(C\),
 +
For ignite number \(C\),
 
the range of allowed \(z\) can be expressed with
 
the range of allowed \(z\) can be expressed with
   
 
\( z-C = r \ \exp(\mathrm i t) \)
  
\( z-C = r \ \exp(\mathrm i t) \)
−  
−
with \( t_{\min}<t<t_{\max}\),
  
   
 
The angle interval \((t_{\min},t_{\max})\) is fixed and does not depend on \(r\).
  
The angle interval \((t_{\min},t_{\max})\) is fixed and does not depend on \(r\).
Line 66: Line 183:
 
in this case, the [[asymptotic]] refers to the approach to value \(C\) from some direction, and it is also [[Sectorial asymptotic]].
  
in this case, the [[asymptotic]] refers to the approach to value \(C\) from some direction, and it is also [[Sectorial asymptotic]].
   
−
===More cases===
 +
==Examples==
−
The definitions above happen to be useful to classify [[asymptotic]]s used
 
−
for the evaluation (and the [[numerical implementation]]) of functions described in book
  
−
«[[Superfunctions]]» <ref name="r">
  
−
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 <br>
  
−
https://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. [[Суперфункции]]. [[Lambert Academic Publishing]], 2014 (In Russian).
  
−
</ref><ref name="e">
  
−
https://www.amazon.com/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 <br>
  
−
https://mizugadro.mydns.jp/BOOK/468.pdf D.Kouznetsov. [[Superfunctions]]. [[Lambert Academic Publishing]], 2020.
  
−
</ref>.
  
   
  +
==Gallery==
−
In general, any restriction of values of \(z\) for the [[asymptotic]] can be specified and the corresponding asymptotic may get the specific name.
  
  +
{{picx|FactoriAsymptoAgreeT.png|200px}}
  +
{{picx|FactorialAsymPlotT.png|200px}}
  +
{{picx|AteSuExq2mapU.png|200px}}
  +
{{picx|AteSuExq2plotU.png|200px}}
  +
{{picx|AteSuFacMapV.png|200px}}
  +
{{picx|AteSuFacPlotU.png|200px}}
   
  +
==Warning==
−
If some kind of restrictions is used many times, then it may have sense to
 
  +
The definition of term «[[Asymtotic]]» in [[TORI]]
−
define a new term to specify the corresponding [[asymptotic]] - in a similar way, as it is done in the subsections above.
  
  +
is «[[outstanding]]», it does not coincide with definition of the term Ato there dictionares, cites, manuals, textbooks.
   
  +
Often, the definition or term «[[asymtotic]]» assumes that function \(A\)
−
However, the researcher is free to invent a new word, any [[Spunk]]<ref>
  
  +
is obtained by truncation of the series with positive or negative power of
−
https://www.imdb.com/title/tt0674923/
  
  +
\(z-z_0\) in the formulas above.
−
[[Pippi hittar en spunk]] // Episode aired Apr 5, 1969.
  
  +
Here, no such an assumption is involved.
−
Director [[Olle Hellbom]] //
  
−
Writer [[Astrid Lindgren]]
  
−
</ref><ref>
  
−
https://www.youtube.com/watch?v=yd45NasMUlI
  
−
[[Pippi hittar en Spunk]]. [[Astrid Lindgren]]/ [[Ingrid Vang Nyman]]. Rabén & Sjögren //
  
−
Peter läser sagor och böcker
  
−
Oct 7, 2022</ref><ref>
  
−
https://www.youtube.com/watch?v=BSyToyrHhh0
  
−
[[Pippi Longstocking]] ([[Astrid Lindgren]]) «[[Spunk]]»!
  
−
movie mag Jan 23, 2018
  
−
</ref>, any «[[Кукарямба]]»<ref>
  
−
https://yapoyu.com/news/magiya-kino/peppi-dlinnyy-chulok-v-poiskah-kukaryamby/ Пеппи Длинный чулок: В поисках кукарямбы. Ровно тридцать лет назад забавная и бойкая девчонка [[Пеппи Длинныйчулок]] из повести [[Астрид Линдгрен]] пережила второе рождение в замечательном фильме режиссёра Маргариты Микаэлян. .. (2026) .. Что за [[кукарямба]], Где о ней прочесть? Сама никогда не слыхивала, Не читывала, не видывала, Но если я её выдумала – Значит, она есть!
  
−
</ref> and give this term some specific meaning required to simplify, to shorten the deduction or the description of some (perhaps also invented) objects.
  
−
The hopes are allowed that the colleagues also find this term appropriate and begin to use it un the same or similar meaning(s).
  
   
  +
Editor tires to make the definition of term «[[asymtotic]]»
−
==Applications==
  
  +
so close to the popular one as possible, while avoiding contradictions.
   
  +
The definition is a draft; it can be modified in order to fill better the
−
Functions \(A\) and \(B\) in the Preamble are assumed to be much simpler to evaluate than the approximated function \(f\).
  
  +
examples of various asymptotics considered.
   
  +
==References==
−
"Fast" growth of \(B\) at \(C\) means that the [[asymptotic]] \(A\) is "good", robust, and is useful for the numeric implementation of function \(f\).
  
  +
{{ref}}
   
  +
https://en.wikipedia.org/wiki/Asymptotic_analysis In mathematical analysis, asymptotic analysis, also known as asymptotics, is a method of describing limiting behavior.
−
The [[asymptotic]] can be presented as a sum, series with indefinite number of terms.
  
   
  +
https://api.pageplace.de/preview/DT0400.9781439864548_A38306604/preview-9781439864548_A38306604.pdf FrankW.J.Olver. Asymptotics and Special Functions Copyright O 1997by A K Peters, Ltd.
−
Then, the asymptotic is called also [[Asymptotic series]].
  
   
  +
https://www.researchgate.net/publication/39064661_Asymptotics_and_Mellin-Barnes_Integrals Asymptotics and Mellin–Barnes Integrals September 2001 DOI:10.1017/CBO9780511546662 Authors: Richard Bruce Paris, David Kaminski// © Cambridge University Press 2001
−
In general, the [[Asymptotic series]] diverge.<br>
  
−
In some special cases ([[Taylor expansion]], [[Laurent series]]), the [[Asymptotic series]] converge, but even in this case the [[radius of convergence]] is limited by the distance to the closest singularity of the [[holomorphic function]] \(f\); and even for an [[entire function]] \(f\) ,
  
−
the [[Taylor expansion]] is not a good representation for the large values of the argument.
  
   
  +
https://dlmf.nist.gov/5.11 NIST Digital Library of Mathematical Functions (2026) 5 Gamma Function // Properties // §5.11(i) Poincaré-Type Expansions
−
For a non-trivial [[special function]], several different [[asymptotic]]s may be required to cover the complex plane with appropriate [[primary approximations]].
  
  +
{{fer}}
−
For example, this is realized in the [[C++]] implementations [[fsexp.cin]] and [[fslog.cin]]
  
−
of the [[natural tetration]] tet and the [[natural arctetration]] ate.
  
   
−
==Acknowledgement==
  
−  
−
[[ChatGPT]] helps to improve this article.
  
−  
−
==References==
  
−
{{ref}}
  
−
https://en.wikipedia.org/wiki/Asymptotic_analysis
  
−
In mathematical analysis, asymptotic analysis, also known as [[asymptotic]]s, is a method of describing limiting behavior.
 
−
{{fer}}
  
 
==Keywords==
  
==Keywords==
  +
 
«[[Agreement]]»,
  
«[[Agreement]]»,
 
«[[Approximation]]»,
  
«[[Approximation]]»,
Line 135: Line 229:
 
«[[Holomorphic function]]»,
  
«[[Holomorphic function]]»,
 
«[[Numerical implementation]]»,
  
«[[Numerical implementation]]»,
−
«[[Primary approximation]]»,
 +
«[[Residual]]»,
−
«[[Asymptotic]]»,
  
 
«[[Sectorial asymptotic]]»,
  
«[[Sectorial asymptotic]]»,
 
«[[Special function]]»,
  
«[[Special function]]»,
 
«[[Spunk]]»,
  
«[[Spunk]]»,
  +
«[[Stirling]]»,
 
«[[Strip asymptotic]]»,
  
«[[Strip asymptotic]]»,
 
«[[Superfunctions]]»,
  
«[[Superfunctions]]»,

Latest revision as of 13:44, 30 January 2026


Warning: this article is under construction.

Asymptotic \(A\) of function \(f\) at point \(z_0\) on the domain \(D\in\mathbb C\) is special kind of approximation, characterized in that, that its quality improves while the input of function, remaining within domain \(D\) approaches \(z_0\). Here, \(z_0\) is either a comlex number or \(\infty\).

Asymptotics are qualified by the criteria of the "quality" of the approximation, by the kind of the limiting point \(z_0\) and by the shape of domain \(D\).

Usually, asympototic \(A\) is easier to evaluate than approximated function \(f\).

Sometimes, for some applications, the properties of asumptotic coincide with those of the approximated function. In these cases, following the last 6th of the TORI asioms, the concept that uses asymtotic, has priority.

Asymototics can be used for fast, qualitative estimates, but also for the precise evaluation of the approximated function.

Apology

There are several various definitions of term «Asymtotic» at various sites, t various dictionaries. Often, term «Asymtotic» is used in an euistic mode, assuming, that «Everybody nows» and with hope, that the professional pure mathematicians understand the problem and redo it with mathematical rugosity.
Often, sigh a hope is not supported with interest and pacience of so-called «pure mathematicians; one example of such a case is resented in the fairy tale «Lesson of quantum topology».
According to legend, the Greatest genius of all centuries and all civilizations gunsek Mao Zedong used to say, that one may count only with own eforts [1]. At the testing of Chinese nuclear weapon, the people were not even alerted. Even worse, it was assumed, that at the use, the significant part of population of China will be dead, and the gensek still will have sufficient number of slaves to maintain his luxury style of life. No any opposition of this idea had been allowed in 1964's China: every citizen could count only whit his own efforts.[2].

Following the Ideas of the Greatest genius of all centuries and all civilizations, this article suggests definition of term Asymptoric in the next section.

Definition

Assume function \(f\) is defined at some domain \(B \in \mathbb C\)

Assume, some point \(z_0\) is specified; it can be a comely number or infinity.

Assume some domain \(D\in B\) is specified.

Assume some special function \(A\) is defined at \(D\).

Assume some holomorphic function \(\tau\) is defined a the set of values of function \(f\).

Let \[ \lim_{z\to z_0, \ z\in D} \Big( \tau\big(f(z)\big) - \tau\big(A(z)\big) \Big) =0 \]

Then, function \(A\) is asymtoric of function \(f\) at domain \(D\) with the criterion function \(\tau\).

The same can be written as follows: \[ f(z) \underset{\mathrm{\tau, \ z\in D,\ z\to z_0}}{\sim} A(z) \]

If function \(\tau\) is not specified, by default, it is assumed to be identity function.

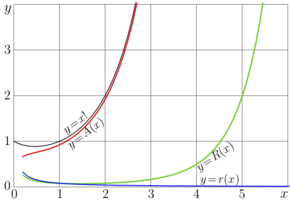
Function \(\ R(z)=f(z)\!-\!A(z) \ \) is called Residual of asymtotic \(A\) of function \(f\)

Function \[\ a(z)=-\lg\left(\frac {|f(z)\!-\!A(z)|} {|f(z)|\!+\!|A(z)|} \right) \]

is called agreement of asymptotic \(A\) with function \(f\).

The agreement gives the criterion of quality of the asymptotic \(A\) at the use as the primary approximation for the numerical implementation of function \(f\).

For the approximation of a function, it is desirable that residual approach zero, and the agreement remain big, say, comparable to the amount of decimal digits that are supported in arithmetic used in the numerical implementation. The most of numerical implementations loaded at TORI provide of order of 14 significant figures.

For some asymptotics, it is not possible to achieve \(R\to 0\).

Then, as criterion, the "small residual" \[ r(z)=\tau(f(z))\!-\!\tau(A(z)) \] can be used; function \[ \alpha (z)= -\lg\left(\frac {|\tau(f(z)) - \tau(A(z))|} {|\tau(f(z))|+ |\tau(A(z))|} \right) \] can be used instead of the agreement; it is desirable to provide small values of \(|r(z)|\) and keep big values of \(\alpha(z)\) at least for \(z\) in vicinity of \(z_0\).

Notes about the definition above

  Fig1802.jpg
\(u\!+\!\mathrm i v\!=\!\mathrm{Filog}(x\!+\mathrm i y)\), bottom of Fig.18.2
in book «Superfunctions»[3][4]

Function \(A\) is supposed to be already known and well described. There is no sense to approximate some unknown function with anther unknown function. Ideally, asymtorotic \(A\) is elementary function, but, generally, it can be any Special function.

In actions, talking about asumtotics, often one does not specify the domain \(D\), assuming, that it is obvious. Usually, it is imlicitly assumed, that \(\tau\) is either identity function or natural logarithm.

In general, some function may have several asymtoirics with different domains \(D\) - especially is \(z_0=\infty\) or \(z_0\) belongs to the branch cut of function \(f\).

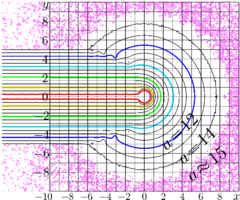
One example of such a function is Filog; its complex map is shown in figure at right.
Filog\((\beta)\) expresses the fixed point of logarithm to base \(b=\mathrm e^\beta\) that is

\(\log_b = (z \!\mapsto\! \log(\beta z))\).

At real \(z_0 < \exp(1/\mathrm d)\), the asymptotic of function Filog depends on the way he input approaches this value.

If we extend the definition of asymptotic and allow the asymptotic to be a function of two arguments, then the tetration to base \(b=\exp(1/\mathrm e)\) can be considered as asymptotic of tetration to base \(b=\exp(\beta)\) while real part of \(\beta\) remains bigger than \(1/\mathrm e\); tetration being considered as function of logarithm of the base is not holomorphic at this point.


Conditional limit

Some restrictios can be applied to values of \(z\) that are allowed in the limit above.

If the imaginary part of \(z\) is assumed to remain in the interval \(a,b\), then, the asymptotic \(A\) is qualified as strip asymptotic.

"Fast" growth of \(B\) at \(C\) means that the asymptotic \(A\) is "good", robust, and is useful for the numeric implementation of function \(f\).

Two special cases of restrictions on values of \(z\) in the limit above are considered in the two subsections below.

Strip asymptotic

For the case of infinite \(C\), it may be assumed that the imaginary part of \(z\) is limited, \(a<\Im(z)<b\) where \(a\) and \(b\) are real number, and it is assumed that \(\Re(z) \to \infty\) or \(\Re(z) \to -\infty\) or \(\Re(z) \to +\infty\).

Then the asympotic \(A\) is qualified as Strip asymptotic.

Sectorial asymptotic

The restriction may refer to the phase of the compass number \(z\); it allowed to have values fro some sector at the complex plane:

\( z = r \ \exp(\mathrm i t) \)

where \(r\) is positive real number and \(t\) is real number from interval \( (t_{\mathrm{min}},t_{\mathrm{max}})\)

Then, the asymtiric \(A\) is qualified as Sectorial asymptotic.

For ignite number \(C\), the range of allowed \(z\) can be expressed with

\( z-C = r \ \exp(\mathrm i t) \)

The angle interval \((t_{\min},t_{\max})\) is fixed and does not depend on \(r\).

in this case, the asymptotic refers to the approach to value \(C\) from some direction, and it is also Sectorial asymptotic.

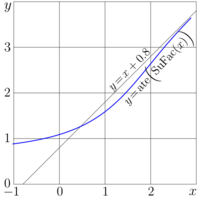
Examples

Gallery

FactoriAsymptoAgreeT.png FactorialAsymPlotT.png AteSuExq2mapU.png AteSuExq2plotU.png AteSuFacMapV.png AteSuFacPlotU.png

Warning

The definition of term «Asymtotic» in TORI is «outstanding», it does not coincide with definition of the term Ato there dictionares, cites, manuals, textbooks.

Often, the definition or term «asymtotic» assumes that function \(A\) is obtained by truncation of the series with positive or negative power of \(z-z_0\) in the formulas above. Here, no such an assumption is involved.

Editor tires to make the definition of term «asymtotic» so close to the popular one as possible, while avoiding contradictions.

The definition is a draft; it can be modified in order to fill better the examples of various asymptotics considered.

References

  1. ↑ https://www.marxists.org/reference/archive/mao/works/red-book/ch21.htm Quotations from Mao Tse Tung 21. Self-Reliance and Arduous Struggle «On what basis should our policy rest? It should rest on our own strength, and that means regeneration through one's own efforts. ..»
  2. ↑ https://www.upi.com/Archives/1964/10/17/Maos-theory-on-atomic-bomb-They-cant-kill-us-all/1653831424805/ UPI ARCHIVES OCTOBER 17, 1964// Mao's theory on atomic bomb: They can't kill us all. TOKYO, Oct. 17, 1964 (UPI) -- Chairman Mao Tse-Tung maintains that Communist China has nothing to fear from nuclear weapons. But his people have paid a fearful price to develop the atomic bomb of their own. Mao is said to have told a Yugoslav visitor to Peking in 1957, "We have a very large territory and a big population. Atomic bombs could not kill all of us." // "What if they killed 300 million of us? We would still have many people left."
  3. ↑ https://www.morebooks.de/shop-ui/shop/product/978-620-2-67286-3 [Superfunctions]]. Lambet Academic Publishing, 2020.
  4. ↑ https://mizugadro.mydns.jp/BOOK/468.pdf D.Kouznetsov. Superfunctions. 2015-2020.

https://en.wikipedia.org/wiki/Asymptotic_analysis In mathematical analysis, asymptotic analysis, also known as asymptotics, is a method of describing limiting behavior.

https://api.pageplace.de/preview/DT0400.9781439864548_A38306604/preview-9781439864548_A38306604.pdf FrankW.J.Olver. Asymptotics and Special Functions Copyright O 1997by A K Peters, Ltd.

https://www.researchgate.net/publication/39064661_Asymptotics_and_Mellin-Barnes_Integrals Asymptotics and Mellin–Barnes Integrals September 2001 DOI:10.1017/CBO9780511546662 Authors: Richard Bruce Paris, David Kaminski// © Cambridge University Press 2001

https://dlmf.nist.gov/5.11 NIST Digital Library of Mathematical Functions (2026) 5 Gamma Function // Properties // §5.11(i) Poincaré-Type Expansions

Retrieved from "https://mizugadro.mydns.jp/t/index.php?title=Asymptotic&oldid=46587"