Difference between revisions of "File:ExpQ2mapT.png"
($ -> \( ; refs ; pre ; keywords) |
|||
| Line 1: | Line 1: | ||
| + | {{oq|ExpQ2mapT.png|Original file (1,765 × 1,729 pixels, file size: 1.15 MB, MIME type: image/png) }} |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| + | \[ |
||
| ⚫ | |||
| ⚫ | |||
| + | \] |
||
| + | |||
| ⚫ | |||
This function is used as [[transfer function]] for the [[tetration to base sqrt(2)]] in the illustration of the application of the method of [[regular iteration]] to construct the [[superfunction]] |
This function is used as [[transfer function]] for the [[tetration to base sqrt(2)]] in the illustration of the application of the method of [[regular iteration]] to construct the [[superfunction]] |
||
| Line 12: | Line 16: | ||
</ref>. |
</ref>. |
||
| + | The map is used as Fig.9.2 at page 104 of book |
||
| − | ==References== |
||
| + | «[[Superfunctions]]», 2020 |
||
| − | <references/> |
||
| + | <ref name="bookA"> |
||
| + | https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. [[Superfunctions]]: Non-integer iterates of holomorphic functions. [[Tetration]] and other [[superfunction]]s. Formulas,algorithms,tables,graphics - [[Lambert Academic Publishing]], 2020/7/28 |
||
| + | </ref><ref name="bookM">https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). [[Superfunctions]]: Non-integer iterates of holomorphic functions. [[Tetration]] and other [[superfunction]]s. Formulas, algorithms, tables, graphics. Publisher: [[Lambert Academic Publishing]]. |
||
| + | </ref><br> |
||
| + | in order to show the periodicity of the exponential. |
||
==[[C++]] generator of curves== |
==[[C++]] generator of curves== |
||
//Files [[ado.cin]] and [[conto.cin]] should be loaded to the working directory in order to compile the [[C++]] code below. |
//Files [[ado.cin]] and [[conto.cin]] should be loaded to the working directory in order to compile the [[C++]] code below. |
||
| + | //<pre> |
||
| − | |||
#include <math.h> |
#include <math.h> |
||
#include <stdio.h> |
#include <stdio.h> |
||
| Line 81: | Line 90: | ||
getchar(); system("killall Preview"); |
getchar(); system("killall Preview"); |
||
} |
} |
||
| + | </pre> |
||
| − | |||
==[[Latex]] generator of labels== |
==[[Latex]] generator of labels== |
||
| + | %<pre> |
||
| − | %<nowiki> %<br> |
||
% file ExpQ2map.pdf should be generated with the code above in order to compile the Latex document below. % |
% file ExpQ2map.pdf should be generated with the code above in order to compile the Latex document below. % |
||
% Copyleft 2012 by Dmitrii Kouznetsov <br> % |
% Copyleft 2012 by Dmitrii Kouznetsov <br> % |
||
| Line 146: | Line 155: | ||
\end{picture}} % <br> |
\end{picture}} % <br> |
||
\end{document} % <br> |
\end{document} % <br> |
||
| − | %</ |
+ | %</pre> |
==References== |
==References== |
||
| + | {{ref}} |
||
| − | <references/> |
||
| + | {{fer}} |
||
| + | ==Keywords== |
||
| + | |||
| + | «[[BaseSqrt2]]», |
||
| + | «[[Exponent]]», |
||
| + | «[[Regular iteration]]», |
||
| + | «[[Superfunctions]]», |
||
| + | «[[Transfer function]]», |
||
| + | «[[Суперфункции]]», |
||
| + | |||
| ⚫ | |||
| ⚫ | |||
[[Category:Book]] |
[[Category:Book]] |
||
[[Category:BookMap]] |
[[Category:BookMap]] |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
[[Category:Complex map]] |
[[Category:Complex map]] |
||
[[Category:C++]] |
[[Category:C++]] |
||
| + | [[Category:Exp]] |
||
[[Category:Latex]] |
[[Category:Latex]] |
||
| + | [[Category:Transfer Function]] |
||
| ⚫ | |||
Latest revision as of 07:51, 23 August 2025
Complex map of exponential to base sqrt2, id est, \(b=\sqrt{2}\);
\[ u\!+\!\mathrm i v=\exp_{\sqrt{2}}(x\!+\!\mathrm i y) \]
Note that lines \(u\!=\!1\), \(u\!=\!2\), \(u\!=\!4\), \(u\!=\!8\) pass through the integer values at the real axis.
This function is used as transfer function for the tetration to base sqrt(2) in the illustration of the application of the method of regular iteration to construct the superfunction [1].
The map is used as Fig.9.2 at page 104 of book
«Superfunctions», 2020
[2][3]
in order to show the periodicity of the exponential.
C++ generator of curves
//Files ado.cin and conto.cin should be loaded to the working directory in order to compile the C++ code below.
// #include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include <complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"
DB B=sqrt(2.);
main(){ int j,k,m,n; DB x,y, p,q, t,r; z_type z,c,d;
r=log(1./(M_E-1.)); printf("r=%16.14f\n",r);
int M=100,M1=M+1;
int N=400,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
FILE *o;o=fopen("ExpQ2map.eps","w");ado(o,162,162);
fprintf(o,"81 81 translate\n 10 10 scale\n");
// DO(m,M1) {X[m]=-8.+.04*(m);
// DO(m,M1) X[m]=log(exp(-8.)+.02*m*(1.+.3*m));
DO(m,M1) X[m]=4.3* sinh( log(4.)*(-1.+.02*m) );
DO(n,N1) Y[n]=-8.+.04*n;
for(m=-8;m<9;m++){if(m==0){M(m,-8.5)L(m,8.5)} else{M(m,-8)L(m,8)}}
for(n=-8;n<9;n++){ M( -8,n)L(8,n)}
fprintf(o,".008 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){g[m*N1+n]=9999; f[m*N1+n]=9999;}
DO(m,M1){x=X[m]; //printf("%5.2f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y);
// c=Tania(z); p=Re(c);q=Im(c);
// c=Shoko(z); p=Re(c);q=Im(c);
// c=ArcShoka(z);
// c=Shoka(c);
c=exp(log(B)*z);
p=Re(c);q=Im(c);
if(p>-99. && p<99. && q>-99. && q<99. ){ g[m*N1+n]=p;f[m*N1+n]=q;}
}}
fprintf(o,"1 setlinejoin 2 setlinecap\n"); p=10;q=1.;
for(m=-4;m<4;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q, q); fprintf(o,".01 W 0 .6 0 RGB S\n");
for(m=0;m<4;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q, q); fprintf(o,".01 W .9 0 0 RGB S\n");
for(m=0;m<4;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q, q); fprintf(o,".01 W 0 0 .9 RGB S\n");
for(m=1;m<9;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p); fprintf(o,".05 W .9 0 0 RGB S\n");
for(m=1;m<9;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".05 W 0 0 .9 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-p,p); fprintf(o,".05 W .6 0 .6 RGB S\n");
for(m=-8;m<9;m++) conto(o,g,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".05 W 0 0 0 RGB S\n");
/*
for(y=-2*M_PI;y<7.;y+=2*M_PI) {
M(0,y)L(-8.1,y) fprintf(o,"0 setlinecap .04 W 1 1 1 RGB S\n");
for(m=0;m<81;m+=4) {x=-.1*m; M(x,y) L(x-.12,y)} fprintf(o,".06 W 1 .5 0 RGB S\n");
for(m=2;m<81;m+=4) {x=-.1*m; M(x,y) L(x-.12,y)} fprintf(o,".06 W 0 .5 1 RGB S\n");
}
*/
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf ExpQ2map.eps");
system( "open ExpQ2map.pdf");
printf("r=%16.14f %16.14f\n",r,sqrt(M_PI*M_PI+r*r));
getchar(); system("killall Preview");
}
Latex generator of labels
%% file ExpQ2map.pdf should be generated with the code above in order to compile the Latex document below. %
% Copyleft 2012 by Dmitrii Kouznetsov <br> %
\documentclass[12pt]{article} % <br>
\usepackage{geometry} % <br>
\usepackage{graphicx} % <br>
\usepackage{rotating} % <br>
\paperwidth 1700pt % <br>
\paperheight 1666pt % <br>
\topmargin -96pt % <br>
\oddsidemargin -8pt % <br>
\textwidth 1700pt % <br>
\textheight 1700pt % <br>
\pagestyle {empty} % <br>
\newcommand \sx {\scalebox} % <br>
\newcommand \rot {\begin{rotate}} % <br>
\newcommand \ero {\end{rotate}} % <br>
\newcommand \ing {\includegraphics} % <br>
\parindent 0pt% <br>
\pagestyle{empty} % <br>
\begin{document} % <br>
\sx{10}{\begin{picture}(162,162) % <br>
\put(1,1){\ing{ExpQ2map}} % <br>
\put(-2,159.9){\sx{.6}{$y$}} <br> %
\put(-2,140){\sx{.6}{$6$}} <br> %
\put(-2,120){\sx{.6}{$4$}} <br> %
\put(-2,100){\sx{.6}{$2$}} <br> %
\put(-2,80){\sx{.6}{$0$}} <br> %
\put(-7,60){\sx{.6}{$-2$}} <br> %
\put(-7,40){\sx{.6}{$-4$}} <br> %
\put(-7,20){\sx{.6}{$-6$}} <br> %
\put(-7, 0){\sx{.6}{$-8$}} <br> %
\put(-4,-3){\sx{.6}{$-8$}} <br> %
\put(16,-3){\sx{.6}{$-6$}} <br> %
\put(36,-3){\sx{.6}{$-4$}} <br> %
\put(56,-3){\sx{.6}{$-2$}} <br> %
\put(81,-3){\sx{.6}{$0$}} <br> %
\put(101,-3){\sx{.6}{$2$}} <br> %
\put(121,-3){\sx{.6}{$4$}} <br> %
\put(141,-3){\sx{.6}{$6$}} <br> %
\put(159.6,-3){\sx{.6}{$x$}} <br> %
\put(13,125.6){\sx{.7}{$u\!=\!0$}} <br> %
\put(13,080.2){\sx{.7}{$v\!=\!0$}} <br> %
\put(13,034.8){\sx{.7}{$u\!=\!0$}} <br> %
\put(38,119){\sx{.6}{\rot{90}$v\!=\!0.2$\ero}} <br> %
\put(58,119){\sx{.6}{\rot{90}$v\!=\!0.4$\ero}} <br> %
\put(84.7,119){\sx{.7}{\rot{90}$v\!=\!1$\ero}} <br> %
\put(104.7,119){\sx{.7}{\rot{90}$v\!=\!2$\ero}} <br> %
\put(116.4,119){\sx{.7}{\rot{90}$v\!=\!3$\ero}} <br> %
% <br> %
\put(38,73){\sx{.6}{\rot{90}$u\!=\!0.2$\ero}} <br> %
\put(58,73){\sx{.6}{\rot{90}$u\!=\!0.4$\ero}} <br> %
\put(84.6,74){\sx{.7}{\rot{90}$u\!=\!1$\ero}} <br> %
\put(104.6,74){\sx{.7}{\rot{90}$u\!=\!2$\ero}} <br> %
\put(116.4,74){\sx{.7}{\rot{90}$u\!=\!3$\ero}} <br> %
% <br> %
\put(39,24){\sx{.6}{\rot{90}$v\!=\!-0.2$\ero}} <br> %
\put(59,24){\sx{.6}{\rot{90}$v\!=\!-0.4$\ero}} <br> %
\put(84.6,26){\sx{.7}{\rot{90}$v\!=\!-1$\ero}} <br> %
\put(104.6,26){\sx{.7}{\rot{90}$v\!=\!-2$\ero}} <br> %
\end{picture}} % <br>
\end{document} % <br>
%
References
- ↑
http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
http://tori.ils.uec.ac.jp/PAPERS/2010sqrt2.pdf D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756. - ↑ https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics - Lambert Academic Publishing, 2020/7/28
- ↑ https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.
Keywords
«BaseSqrt2», «Exponent», «Regular iteration», «Superfunctions», «Transfer function», «Суперфункции»,
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 17:50, 20 June 2013 | 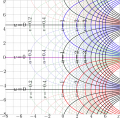 | 1,765 × 1,729 (1.15 MB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
The following page uses this file: