Search results

Create the page "Complex analysis" on this wiki! See also the search results found.

• Mandelbrot polynomial
  whrere \(c\) is parameter. Usially, it is assumed to be a [[complex number]]. ...be integer; the [[Mandelbrot polynomial]] can be iterated arbitrary (even complex) number of times.
  2 KB (229 words) - 18:44, 30 July 2019
• Superfunctions
  [[Complex map]]: truncated Taylor expansion of abelsine [[AuSin]], Fig.22.2</p></cent At the front cover, the [[complex map]] of [[natural tetration]] is shown.
  15 KB (2,166 words) - 20:33, 16 July 2023
• Linear fuction
  where \(A\) and \(B\) are constants (for example some complex numbers) ...r. As other holomophic functions, the linear function can be iterated even complex number of times.
  2 KB (234 words) - 18:43, 30 July 2019

• File:Amosmap.jpg [[Complex map]] of function [[amos]], that determines (for integer values of its argu ...ional (and non–necessary) cut lines, that males difficult the asymptotic analysis; so, for this application, representation through [[Lof]] may be more conve (1,726 × 1,718 (396 KB)) - 08:29, 1 December 2018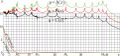

• File:Norifit76fragment.jpg Analysis of the approximation of [[nori function]] through function [[korifit76]], #include <complex> (967 × 448 (155 KB)) - 08:44, 1 December 2018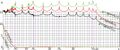

• File:Norifit76plot.jpg Analysis of the approximation of [[nori function]] through function [[korifit76]], #include <complex> (1,070 × 448 (168 KB)) - 08:44, 1 December 2018

• File:Susinmap8t.jpg [[Complex map]] of the primary approximation of function [[SuSin]] with parameter $M= into equation $~f(z\!+\!1)=\sin(f(z))~$ and the asymptotic analysis at large $z$. Then, (4,312 × 4,283 (1.78 MB)) - 08:53, 1 December 2018

• Ackermann function
  For given complex number \(b\), called "base", and given integer number \(n\), called "number ...this case is easier to interpret and to apply in physics, than cases with complex \(b\).
  10 KB (1,534 words) - 06:44, 20 July 2020
• Amos
  Below the complex map of function [[Amos]] is shown with lines of its content real part and l ...necessary for [[summation of the asymptotic series]], the extension to the complex plane is essential. For this reason, the special name is required for the h
  6 KB (883 words) - 18:44, 30 July 2019
• ArqNem
  ==Complex maps== Complex maps of function \(\mathrm{ArqNem}_q(z)\) is shown in figures at right for
  7 KB (1,319 words) - 18:46, 30 July 2019
• AuNem
  For \(q\!=\!0\), \(q\!=\!1\) and \(q\!=\!2\), [[complex map]] of function \(\mathrm{AuNem}_q\) is shown in figures 2,3,4. Coefficients \(c\) can be found from the asymptotic analysis of equaiton \(\mathrm{SuNe}_q(\mathrm{AuNe}(z))=0\).
  9 KB (1,441 words) - 18:45, 30 July 2019
• AuSin
  ...n of the expansion to the Abel equation and the straightforward asymptotic analysis. ...nt of this implementation with that of function [[SuSin]] is seen from the complex map of function
  5 KB (761 words) - 18:48, 30 July 2019
• Base e1e
  [[File:Expe1emapT1000.jpg|200px|thumb|[[Complex map|Map]] of \(~f\!=\!\eta\!=\!\exp_{\exp(1/\mathrm e)}~\); here \(~u+\math [[File:Loge1emapT1000.jpg|200px|thumb|[[Complex map|Map]] of \(~f\!=\!\log_{\exp(1/\mathrm e)}~\); here \(~u+\mathrm i v=f(
  4 KB (559 words) - 17:10, 10 August 2020
• Kori
  Explicit plot and [[complex map]] of function [[kori]] are shown in figures at right. Kori is [[entire function]], it is holomorphic in the whole complex plane. The zero in the denominator in the definition is compensated with th
  14 KB (1,943 words) - 18:48, 30 July 2019
• Lof
  ...\big(\)[[Factorial]]\((z)\big)~\) , that is holomorphic in the most of the complex \(z\) plane (except \(z\!\le\!-1\)). [[Complex map]] of function [[lof]] is shown in figure at right with lines \(u\!+\!\m
  3 KB (478 words) - 18:43, 30 July 2019
• Maga
  ...st option, the holomorphic properties of the functions involved (and their complex maps) should be analysed. ...tation indicates the way of holomorphic extension of function [[maga]] for complex values of the argument \(z\); the appropriate paths of integration should b
  8 KB (1,256 words) - 18:44, 30 July 2019
• Mathematics of Computation
  numerical analysis, computational discrete mathematics, number theory, algebra, combinatorics, D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670.
  2 KB (344 words) - 07:02, 1 December 2018
• Morinaga function
  Below, the [[complex map]] of the [[Morinaga function]] is compared to that of function [[Bessel ...errors limit the range of applicability of this expansion. With double (or complex double) variables, with \(M\!=\!16\) , while last term with coefficient \(c
  15 KB (2,303 words) - 18:47, 30 July 2019
• Naga
  For complex \(p\), expression ...cation mentioned above refers only to the real values of the argument. The analysis of the holomorphic properties of the functions involved is supposed to reve
  5 KB (750 words) - 10:00, 20 July 2020
• NemBran
  ...[Nemtsov function]] \(\mathrm{Nem}_q\) versus parameter \(q\). While, only analysis for the real \(q\) is presented. For real \(q\) function \(\mathrm{Nem}_q\) ...ns should be implemented in the most of the complex plane, id est, for the complex argument.
  3 KB (400 words) - 18:48, 30 July 2019

View (previous 20 | next 20) (20 | 50 | 100 | 250 | 500)