File:Figlogzo2t.jpg

Large version of this map

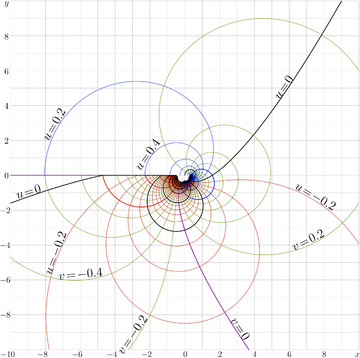
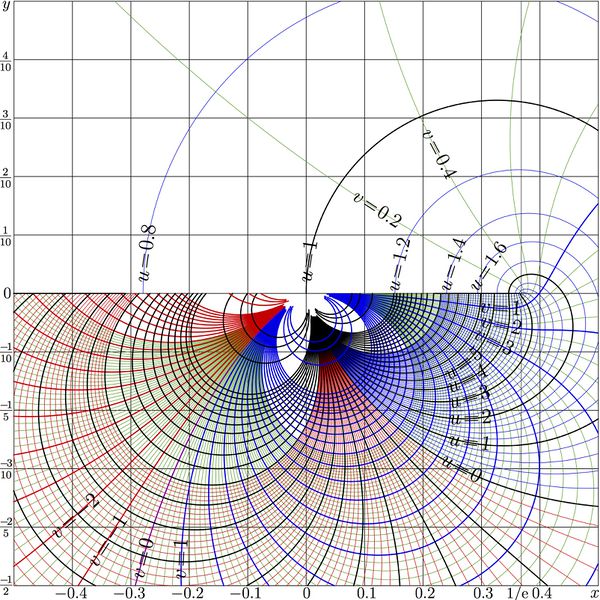
Bottom part of Fig.18.2 at page 247 of book «Superfunctions» ^[1], 2020.

The same picture appears also as the bottom part of Pic.18.2 at page 255 of the Russian version «Суперфункции» ^[2], 2014.

The figure shows the complex map of function Filog, zoomin of the square of size unity from the central part of figure at right, http://mizugadro.mydns.jp/t/index.php/File:Filogbigmap100.png

The function is shown in the standard for TORI way: \[ u\!+\!\mathrm i v= \mathrm{Filog} (x\!+\!\mathrm i y) \] Lines of constant \(u\) and
lines of constant \(v\) are drawn in the \(x\),\(y\) plane.

Meaning

\[ z=\mathrm{Filog}(a) \]

expresses solution \(z\) of equation \[ \ln(z)/a=z \] This solution is described in article «Filog» and in book «Superfunctions» ^[1]

Function Filog allows to evaluate two fixed points \(L\) of logarithm to base \(b\) as follows: \[ L=\mathrm{Filog}\big( \ln(b)\big) \] and \[ L=\mathrm{Filog}\big( \ln(b^*)\big)^* \]

C++ generator of curves

// Files ado.cin, conto.cin, filog.cin, tania.cin should be loaded in order to compile the C++ code below

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include <complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"
#include "filog.cin"
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
int M=500,M1=M+1;
int N=501,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
FILE *o;o=fopen("filogzo2.eps","w");ado(o,1020,1020);
fprintf(o,"510 510 translate\n 1000 1000 scale\n");
DO(m,M1) X[m]=-.5+.002*(m-.2);
DO(n,250)Y[n]=-.5+.002*n;
        Y[250]=-.00001;
        Y[251]= .00001;
for(n=252;n<N1;n++) Y[n]=-.5+.002*(n-1.);

for(m=-5;m<6;m++){M(.1*m,-.5)L(.1*m,.5)}
for(n=-5;n<6;n++){M( -.5,.1*n)L(.5,.1*n)}
fprintf(o,"2 setlinecap .001 W 0 0 0 RGB S\n");
M(exp(-1.),-.5)
L(exp(-1.), .5)
//M(M_PI/2.,-.5)
//L(M_PI/2., .5)
fprintf(o,".0007 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){g[m*N1+n]=9999; f[m*N1+n]=9999;}
DO(m,M1){x=X[m]; //printf("%5.2f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y);        
// c=Tania(z_type(-1.,-M_PI)+log(z))/(-z); 
c=Filog(z);
p=Re(c);q=Im(c);  
if(p>-201. && p<201. &&  q>-201. && q<201. ){ g[m*N1+n]=p;f[m*N1+n]=q;}
       }}
fprintf(o,"1 setlinejoin 1 setlinecap\n");  p=5.;q=1;
for(m=-10;m<10;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q, q); fprintf(o,".0008 W 0 .6 0 RGB S\n");
for(m=0;m<10;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q, q); fprintf(o,".0008 W .9 0 0 RGB S\n");
for(m=0;m<10;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q, q); fprintf(o,".0008 W 0 0 .9 RGB S\n");
for(m=1;m<20;m++)  conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p); fprintf(o,".002 W .9 0 0 RGB S\n");
for(m=1;m<20;m++)  conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".002 W 0 0 .9 RGB S\n");
                  conto(o,f,w,v,X,Y,M,N, (0.  ),-p,p); fprintf(o,".002 W .6 0 .6 RGB S\n");
for(m=-20;m<21;m++) conto(o,g,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".002 W 0 0 0 RGB S\n");
p=10.;
conto(o,g,w,v,X,Y,M,N, 30 ,-p,p); fprintf(o,".002 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, 40 ,-p,p); fprintf(o,".002 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, 50 ,-p,p); fprintf(o,".002 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,-30 ,-p,p); fprintf(o,".002 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,-40 ,-p,p); fprintf(o,".002 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,-50 ,-p,p); fprintf(o,".002 W 0 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, -30,-p,p); fprintf(o,".002 W .9 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, -40,-p,p); fprintf(o,".002 W .9 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, -50,-p,p); fprintf(o,".002 W .9 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, 30,-p,p); fprintf(o,".002 W 0 0 .9 RGB S\n");
conto(o,f,w,v,X,Y,M,N, 40,-p,p); fprintf(o,".002 W 0 0 .9 RGB S\n");
conto(o,f,w,v,X,Y,M,N, 50,-p,p); fprintf(o,".002 W 0 0 .9 RGB S\n");

fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
      system("epstopdf filogzo2.eps");    
     system(    "open filogzo2.pdf"); //for mac
//    getchar(); system("killall Preview"); // for mac
// Copyleft 2012 by Dmitrii Kouznetsov
}

Latex generator of labels

\documentclass[12pt]{article}
\usepackage{geometry}
\paperwidth 1030pt
\paperheight 1030pt
\textwidth 1140pt
\textheight 1140pt
\topmargin -103pt
\oddsidemargin -86pt
\usepackage{graphicx}
\usepackage{rotating}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \rme {\mathrm{e}}
\newcommand \sx {\scalebox}
\begin{document}
\begin{picture}(1020,1020)
\put(10,10){\includegraphics{filogzo2}}

\put(0,1012){\sx{2.3}{$y$}}
\put(-7,914){\sx{2.3}{$\frac{4}{10}$}}
\put(-7,814){\sx{2.3}{$\frac{3}{10}$}}
\put(-7,714){\sx{2.3}{$\frac{2}{10}$}}
\put(-7,614){\sx{2.3}{$\frac{1}{10}$}}
\put( 2,514){\sx{2.3}{$0$}}
\put(-7,414){\sx{2.3}{$\frac{-\!1}{10}$}}
\put(-7,314){\sx{2.3}{$\frac{-\!1}{5}$}}
\put(-7,214){\sx{2.3}{$\frac{-\!3}{10}$}}
\put(-7,114){\sx{2.3}{$\frac{-\!2}{5}$}}
\put(-7, 14){\sx{2.3}{$\frac{-\!1}{2}$}}
\put(90, -1){\sx{2.3}{$-0.4$}}
\put(190, -1){\sx{2.3}{$-0.3$}}
\put(290, -1){\sx{2.3}{$-0.2$}}
\put(390, -1){\sx{2.3}{$-0.1$}}
\put(516, -1){\sx{2.3}{$0$}}
\put(609, -1){\sx{2.3}{$0.1$}}
\put(709, -1){\sx{2.3}{$0.2$}}
\put(809, -1){\sx{2.3}{$0.3$}}
\put(866, -1){\sx{2.2}{$1/\mathrm e$}}
\put(910, -1){\sx{2.3}{$0.4$}}
\put(1010, 0){\sx{2.4}{$x$}}
\put(250,540){\sx{3}{\rot{82}$u\!=\!0.8$ \ero} }
\put(530,540){\sx{3}{\rot{81}$u\!=\!1$ \ero} }
\put(680,524){\sx{2.8}{\rot{77}$u\!=\!1.2$ \ero} }
\put(768,524){\sx{2.8}{\rot{72}$u\!=\!1.4$ \ero} }
\put(816,524){\sx{2.8}{\rot{56}$u\!=\!1.6$ \ero} }
\put(600,684){\sx{2.8}{\rot{-33}$v\!=\!0.2$ \ero} }
\put(720,798){\sx{2.8}{\rot{-62}$v\!=\!0.4$ \ero} }
\put(820,490){\sx{3}{\rot{-4}$v\!=\!1$ \ero} }
\put(820,466){\sx{3}{\rot{-12}$v\!=\!2$ \ero} }
\put(808,446){\sx{3}{\rot{-26}$v\!=\!3$ \ero} }
\put(768,372){\sx{3}{\rot{36}$u\!=\!5$ \ero} }
\put(770,350){\sx{3}{\rot{26}$u\!=\!4$ \ero} }
\put(770,324){\sx{3}{\rot{16}$u\!=\!3$ \ero} }
\put(768,297){\sx{3}{\rot{2}$u\!=\!2$ \ero} }
\put(766,262){\sx{3}{\rot{-8}$u\!=\!1$ \ero} }
\put(752,230){\sx{3}{\rot{-28}$u\!=\!0$ \ero} }

\put(94,99){\sx{3}{\rot{41}$v\!=\!-2$ \ero} }
\put(162,50){\sx{3}{\rot{57}$v\!=\!-1$ \ero} }
\put(242,30){\sx{3}{\rot{75}$v\!=\!0$ \ero} }
\put(315,30){\sx{3}{\rot{87}$v\!=\!1$ \ero} }

\end{picture}
\end{document}  

Similar pictures

Fig.18.2 generated with «Conrec6.cin»

Similar complex map is generated as test of routine «Conrec6.cin».

It is shown in figure at right.

The same set of labels is used in both pictures.

These pictures are compared in articles «Conrec6 demo‎», «MapConrec6demo‎‎»; no visual difference is seen, the pictures look the same.

In this sense, routines «Conrec6.cin» and «Conto.cin» are equivalent.

References

Keywords

«Book», «C++», «Complex map», «Filog», «Fixed point», «Latex», «Logarithm», «Superfunctions», «Tetration», «Zoom»,

«Суперфункции»,