File:SuTraAsy3plotT.png

Summary

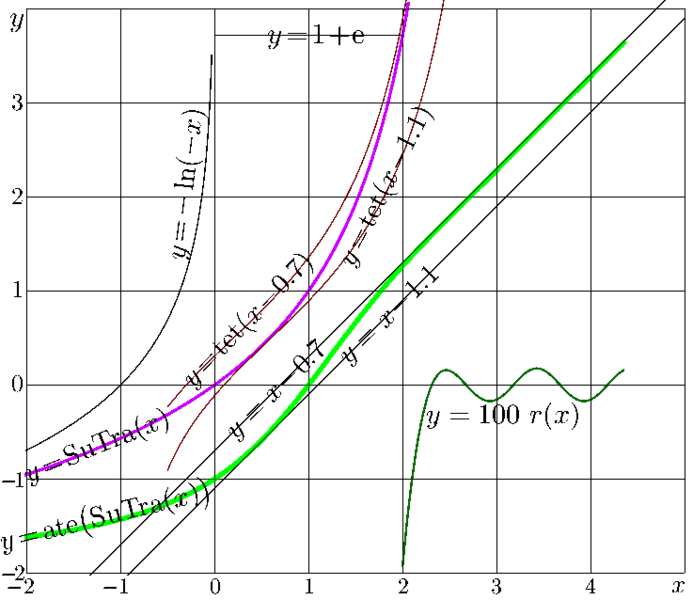
Explicit plot of function SuTra of real input, pink curve \(\ y=\mathrm{SuTra}(x) \ \) and its asymptotics.

SuTra is superfunction for the Trappmann function \( \ z\mapsto z\!+\!\exp(z)\ \).
Function SuTra is specified as «Entire Function with Logarithmic Asymptotic».
It is described in book «Superfunctions»^[1], 2020 and also in Applied Mathematical Sciences ^[2], 2013.

At large negative values of the input, \[ \mathrm{SuTra}(x) \underset{\ x\to -\infty}{\Large \sim} -\ln(-x) \] Asymptotic \(\ y\!=\! -\ln(-x) \ \) is shown with thin black curve.

The thin horizontal line at the top shows value of SuTra at the specific value of the input, \( \mathrm{SuTra}(2)=1+\mathrm e\approx 3.71 \ \)

The thick green curve shows the combination of Natural ArcTetration \( \mathrm{ate}\) and function SuTra.

The Natural ArcTetration is described in the same book «Superfunctions»^[1], but also in Journal Mathematics of Computation ^[3], 2009 and in the Vladikavkaz Mathematical Journal ^[4], 2010.

Other lines represent the conjectures, hypotheses, speculations about the asympototic behavior of function SuTra. These conjectures are based on the observation, that in the right hand side of the picture, the thick green line looks almost straight.

Conjectures

The picture hints to the conjectures.

Conjecture 1: For a real number \(x\), the inequality takes place: \( \mathrm{ate}\big(\mathrm{SuTra}(x)\big) > x - 1.1 \)

Conjecture 2: For a positive \(x\), the inequality takes place: \(\ \mathrm{ate}\big(\mathrm{SuTra}(x)\big) < x - 0.7 \)

Strips

Dependence \(\ y\!=\!x-1.1 \ \) and dependence \( \ y\!=\!x-0.7 \) are sown with thin black straight lines.

Apparently, in the right hand side of the picture, \( \mathrm{ate}\big(\mathrm{SuTra}(x)\big) \) happens within the strip \[ x-1.1 < \mathrm{ate}\big(\mathrm{SuTra}(x)\big) < x - 0.7 \]

Applying the natural tetration \(\mathrm{tet}\) to all sides of this inequality, we get the strip for function SuTra: \[ \mathrm{tet}(x\!-\!1.1) < \mathrm{SuTra}(x)\big) < \mathrm{tet}(x\!-\!0.7) \] Dependences \(\ y=\mathrm{ate}(x\!-\!1.1) \ \) and \(\ y=\mathrm{ate}(x\!-\!0.7) \ \) are shown with thin brown curves.

Hypothesis 3

One may think, that there exist positive number \(x_{\mathrm {st}} \approx 0.715316\) such that \[ \mathrm{SuTra}(x) \overset{\mathrm{ate}} {\underset{ x\to +\infty}{\Large\sim}} \mathrm{tet}(x\!-\!x_{\mathrm {st}} ) \] in sense, that \[\ \mathrm{ate}\big(\mathrm{SuTra}(z) \big) - (x\!-\!x_{\mathrm {st}}) \to 0 \ \]

Indeed, the computation show that the agreement \[ a(x) = -\lg \left( \frac {\big| \mathrm{ate}\big(\mathrm{SuTra}(z) \big) - (x- 0.715316) \big|} {\big| \mathrm{ate}\big(\mathrm{SuTra}(z) \big)\big| + |x- 0.715316|} \right) \] grows, at least while the (double) variables still allow to perform the computations.

As for the residual \[ r(x) = \mathrm{ate}\big(\mathrm{SuTra}(z) \big) - (x- 0.715316) \] it does not show so "patriotic" behavior. Instead, \(r(x)\) oscillates with quasiperiod of order of unity; two oscillations are seen in the picture.
In order to show this residual, it is scaled with factor 100; depencence \[ \ y\!=\! 100 \ r(x) \ \] is shown with thin dark green curve in the right-bottom side of the picture.

In such a way, the Conjecture 3 is refuted. However, in sense of agreement \( \displaystyle a(x) = -\lg \left( \frac {\big| \mathrm{ate}\big(\mathrm{SuTra}(x) \big) - \mathrm{ate}(A(x)) \big|} {\big| \mathrm{ate}\big(\mathrm{SuTra}(x) \big)\big| + |\mathrm{ate}(A(x))|} \right) \ \),
the approximatom \[A(z)=\mathrm{tet}(z-x_{\mathrm {st}}) \] still can be considered as a "weak asymptotic" of function SuTra.

There are 9 lines shown above. Perhaps they are too many for a single picture. One can load the generator below and suppress some of the lines.

The generator below is copilefld. Please attribute the source at the reuse. The attribution helps to trace (and to correct) mistakes if any.

C++

/* subroutines ado.cin, Tania.cin, LambertW.cin, SuZex.cin, fsexp.cin fslog.cin should be loaded in order to compile the source below.

uZex.cin, fslog.cin should be loaded in order to compile the source below.
*/
//
 #include <math.h>
 #include <stdio.h>
 #include <stdlib.h>
 #define DB double
 #define DO(x,y) for(x=0;x<y;x++)
 using namespace std;
 #include<complex>
 typedef complex<double> z_type;
 #define Re(x) x.real()
 #define Im(x) x.imag()
 #define I z_type(0.,1.)
 #include "Tania.cin" // need for LambertW
 #include "LambertW.cin" // need for AuZex
 #include "SuZex.cin"
 #include "fslog.cin"
 #include "fsexp.cin"
 //#include "AuZex.cin"

 z_type tra(z_type z){ return exp(z)+z;}

 //z_type F(z_type z){ return log(suzex(z));}
 //z_type G(z_type z){ return auzex(exp(z));}

 z_type sutra(z_type z){ if( Re(z)<2. || fabs(Im(z))>2. ) return log(suzex(z));
                                                          return tra(sutra(z-1.));}
 #include "ado.cin"
 #define M(x,y) fprintf(o,"%6.4f %6.4f M\n",0.+x,0.+y);
 #define L(x,y) fprintf(o,"%6.4f %6.4f L\n",0.+x,0.+y);
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;  
//FILE *o;o=fopen("SuTraPlo3.eps","w");  ado(o,812,812);
//FILE *o;o=fopen("19.eps","w");  ado(o,712,612);
FILE *o;o=fopen("SuTraAsy3plot.eps","w");  ado(o,712,612);
//FILE *o;o=fopen("03.eps","w");  ado(o,712,612);
 fprintf(o,"202 202 translate\n 100 100 scale\n");
 fprintf(o,"1 setlinejoin 2 setlinecap\n");

 DO(m,240){x=-2.02+.02*m; y=Re(sutra(x)); if(m==0) M(x,y) else L(x,y) if(x>5.03||y>4) break;} fprintf(o,".03 W .8 0 1 RGB S\n");
 DO(m,240){x=-.5+.02*m; y=Re(FSEXP(x-.7)); if(m==0) M(x,y) else L(x,y) if(x>5.03||y>4) break;} fprintf(o,".01 W .5 0 0 RGB S\n");
 DO(m,240){x=-.5+.02*m; y=Re(FSEXP(x-1.1)); if(m==0) M(x,y) else L(x,y) if(x>5.03||y>4) break;} fprintf(o,".01 W .5 0 0 RGB S\n");
 DO(m,100){x=-2.01+.02*m; y=-log(-x);     if(m==0) M(x,y) else L(x,y) if(x>5.03||y>4) break;} fprintf(o,".01 W 0 0 0 RGB S\n"); 
// DO(m,74){x=-2.02+.1*m; y=Re(FSLOG(x));  if(m==0) M(x,y) else L(x,y) if(x>5.03||y>4) break;} fprintf(o,".02 W 1 0 0 RGB S\n"); 
 DO(m,65){x=-2.05+.1*m; y=Re(FSLOG(sutra(x))); if(m==0) M(x,y) else L(x,y) if(x>5.03||y>4) break;} fprintf(o,".05 W 0 1 0 RGB S\n"); 

// DO(m,240){x=2-.05+.01*m; y=Re(FSLOG(sutra(x-I*.001))) - (x-.715316+.00174*sin(2*M_PI*(x-.177))); y*=10000 ; if(m==0) M(x,y) else L(x,y) } fprintf(o,".02 W 0 0 1 RGB S\n"); 
 DO(m,236){x=2.0+.01*m; y=Re(FSLOG(sutra(x))) - (x-.715316); y*=100; if(m==0) M(x,y) else L(x,y) } fprintf(o,".02 W 0 .4 0 RGB S\n"); 

M(-2,-2-.7)L(5,5-.7) fprintf(o,".002 W 0 0 0 RGB S\n");
M(-1,-1-1.1)L(5,5-1.1) fprintf(o,".002 W 0 0 0 RGB S\n");

 for(n=-2;n<5;n++) {M(-2,n)L(5,n)}
 for(m=-2;m<6;m++) {M(m,-2)L(m,4)}
 // M(M_E,0)L(M_E,1) M(0,M_E)L(1,M_E)  
 M(0,1.+M_E) L(2,1.+M_E)
 fprintf(o,".003 W S\n");

fprintf(o,"showpage\n"); fprintf(o,"%c%cTrailer\n",'%','%');  fclose(o);
      system("epstopdf SuTraAsy3plot.eps"); 
      system(    "open SuTraAsy3plot.pdf"); //for macintosh
//      getchar(); system("killall Preview"); // For macintosh
return 0;
}
//

Latex

\documentclass[12pr]{article}
\paperwidth 740pt
\paperheight 640pt
\textwidth 800pt
\textheight 700pt
\topmargin -96pt
\oddsidemargin -66pt
%\usepackage{xcolor}
\usepackage{graphicx}
\usepackage{rotating}
\newcommand \sx {\scalebox}
\newcommand \ing {\includegraphics}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\parindent 0pt
\begin{document}
\begin{picture}(720,620)
%\put(-2,-6){\textcolor{white}{\rule{740pt}{740pt}}}
\put(20,20){\ing{SuTraAsy3plot}}
%\put(20,20){\ing{01}}
\put( 4,606){\sx{3.1}{\(y\)}}
\put(279,587){\sx{3.1}{\(y\!=\!1\!+\!\mathrm e\)}}
\put( 6,516){\sx{2.6}{\(3\)}}
\put( 6,416){\sx{2.6}{\(2\)}}
\put( 6,316){\sx{2.6}{\(1\)}}
\put( 6,216){\sx{2.6}{\(0\)}}
\put(-6,114){\sx{2.4}{\(-\!1\)}}
\put(-6,14){\sx{2.4}{\(-\!2\)}}
\put(0,0){\sx{2.4}{\(-2\)}}
\put(102,0){\sx{2.4}{\(-1\)}}
\put(218,0){\sx{2.4}{\(0\)}}
\put(318,0){\sx{2.4}{\(1\)}}
\put(418,0){\sx{2.4}{\(2\)}}
\put(518,0){\sx{2.4}{\(3\)}}
\put(618,0){\sx{2.4}{\(4\)}}
\put(710,1){\sx{2.7}{\(x\)}}
\put(190,356){\sx{3}{\rot{83}\(y\!=\!-\ln(-x)\)\ero}}
%\put(155,276){\sx{2.6}{\rot{72}\(y=-\ln(-x)\)\ero}}
\put(370,348){\sx{3}{\rot{63}\(y\!=\!\mathrm{tet}(x\!-\!1.1)\)\ero}}
\put(199,219){\sx{3}{\rot{46}\(y\!=\!\mathrm{tet}(x\!-\!0.7)\)\ero}}
%\put(232,240){\sx{2.6}{\rot{48}\(y=\mathrm{SuTra}(x)\)\ero}}
\put(24,119){\sx{3}{\rot{22}\(y\!=\!\mathrm{SuTra}(x)\)\ero}}
\put(245,164){\sx{3}{\rot{44}\(y=x\!-\!0.7\)\ero}}
\put(365,244){\sx{3}{\rot{44}\(y=x\!-\!1.1\)\ero}}

\put(-4,46){\sx{3}{\rot{14}\(y\!=\!\mathrm{ate}\big(\mathrm{SuTra}(x)\big)\)\ero}}

\put(448,182){\sx{3}{\rot{0}\(y=100 \ r(x)\)\ero}}
\end{picture}
\end{document}

References

Keywords

«ado.cin», «fslog.cin», «LambertW.cin», «Tania.cin», «SuZex.cin»,

«Arctetral asymptotic», «Arctetration», «Asymptotic», «Superfunction», «Superfunctions», «SuTra», «Trappmann function»,