Ackermann function

Ackermann function is defined in a little bit different way in various sources. In TORI the definition is suggested, that is oriented to the application for the theory of superfunctions, and it is different from that used in the Computability theory. While no commonly accepted system of notations is established, at the reference to the Ackermann function, either the definition, or, at least, link should be provided.

In order to simplify the use in formulas, the writing with lower case letter, ackermann, refers to the Ackermann function. Beeng written with capital, Ackermann, this word may refer to famous scientist Wilhelm Ackermann.

The most of content of this article is published in 2014 at Applied and Computational Mathematics

Definition

For given complex number \(b\), called "base", and given integer number \(n\), called "number of Ackermann", function \(A_{b,n}(z)\) is called Ackermann function, iff it satisfies the following equations:

\(A_{b,1}(z)=b+z\)

\(A_{b,n}(1) = b~ ~\) for \(~ n\!>\!1\)

\(A_{b,n}(z\!+\!1)=A_{b,n-1}\big( A_{b,n}(z) \Big)\)

The last equation can be referred also as transfer equation.

Often, it is assumed, that base \(b\) is real number, bigger than unity; this case is easier to interpret and to apply in physics, than cases with complex \(b\).

\(A_{b,1}\) is referred aslo as the First ackermann, \(A_{b,2}\) can be called "second ackermann", and so on.

In this system of notations, each ackermann \(A_{b,n}\) appears as transfer function in the transfer equation for \(A_{b,n+1}\).

Notations

The first ackermann functions have special names:

\(A_{b,1}(z)=b + z\) , addition of constant \(b\)

\(A_{b,2}(z)=b \,z\) , multiplication to constant \(b\)

\(A_{b,3}(z)=b^z~\) , exponent to base \(b\)

\(A_{b,4}(z)=\mathrm{tet}_b(z)~\) , tetration to base \(b\)

\(A_{b,5}(z)=\mathrm{pen}_b(z)~\) , pentation to base \(b\)

and so on. The most of the school–level Algebra and significant part of mathematical analysis are based on the first 3 ackermann functions and their inverse functions in various combinations.

Construction and analysis of higher ackermanns, beginning with tetration, is under development since century 20 and, for integer values of base and argument, even earlier. .

Holomorphic extension for tetration (to base e) had been reported only in 2009 .

Binary ackermanns, special notation

Comparison of notations for binary ackermanns: \(y\!=\!A_{2,m}(x)\), thick curves, and \(y\!=\!\mathcal A(m,x)\), thick curves

For the base \(b\!=\!2\), the ackermann is called binary, or classical. For this base (or for this case) there exist another and more popular notation,

\( A_{2,m}(z) = \mathcal A (m,z\!+\!3)-3\)

In particular,

\(A_{2,1}=2+x=\mathcal A(1,x\!+\!3)-3=\mathcal A(1,x)\)

\(A_{2,2}=2x=\mathcal A(2,x\!+\!3)-3\)

\(A_{2,3}=\exp_2(x)=\mathcal A(3,x\!+\!3)-3=2^x\)

\(A_{2,4}=\mathrm{tet}_2(x)=\mathcal A(3,x\!+\!3)-3\)

In order to avoid confusions, if character A refers to the base 2, and the notation without subscripts is used, this character should appear with Calligraphic font. In Latex (and in TORI), this name can be typed as "\mathcal A".

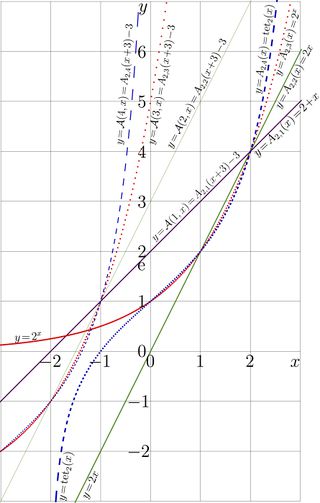
In order to make the relations between the two systems of notations for the ackermann functions, both, Italics \(A\) and Calligraphic \(\mathcal A\), both functions are plotted in the figure at right for the real values of the last argument.

The curves for the binary ackermanns \(y\!=\!A_{2,m}(x)\) are shown with thick lines; they pass through the point \((2,4)\).

The curves for the canonical binary ackermanns \(y\!=\!\mathcal A(m,x)\); are shown with thin lines; they pass through the point \((-1,1)\).

The thin curves in the figure can be obtained with just translation \(x\rightarrow x\!-\!3\), \(y\rightarrow y\!-\!3\).

For the binary ackermanns, the chain of basic equations can be slightly extended, including the Zeroth ackermann, in the gollowing way:

\(A(0,z)=z++\)

\(A(m\!+\!1,0)=A(m,1)\)

\(A(m\!+\!1,z)=A\Big(m,A(m\!+\!1,z)\Big)\)

As in the case of the notations with subscript, the last equation specifies, each new ackermann, been considered as holomorphic function of the second (id est, the last) argument is superfunction with respect to the previous one; and the only zeroth ackermann is exception.

More about notations

Equations for \(\mathcal A\) can be also considered as definition of ackermanns to base 2. The equation for this spatial case are more classical, canonical, because in this way they usually appear in the literature for the Ackermann dunctions. In TORI, aiming the application for iteration of exponential, the match with exponent, tetration and pentation is more important; for this, the misplacement of both the argument and value of functions for constant \(3\) is not used, in such a way, so, the 3d ackermann is just exponential, the 4d one is just tetration, and so on.

The TORI notations are important for the occasions when the name of the function appear without argument, but the order still should be specified. The nth iteration of the mth binary ackermann can be written as

\(\Big(z\mapsto\mathcal A(m, z\!+\!3)\!-\!3\Big)^n\)

However, this notation is much longer than the equivalent \(A_m^{\,n}\).

For the allowance with other sources, the relation

\(~\mathcal A(m,n)=A_{2,m}(z\!+\!3)\!-\!3~\) should be kept in mind.

Natural ackermanns

FIrst five ackermanns to base e: \(~ ~y\!=\!A_{\mathrm e,n}(x)\) versux \(x\) for \(n\!=\!1,2,3,4,5\)

In analogy with natural exponent and natural logarithm, ackermanns to base \(\exp(1)=\mathrm e \approx 2.71\) are called "natural", although in other context the word natural may have pretty different meanings. If the base is \(\mathrm e\), it may be omitted, and, by default, if it is omitted, it is assumed to be e.

\(A_{\mathrm e,1}(z)=\mathrm e + z\)

\(A_{\mathrm e,2}(z)=\mathrm e \,z\)

\(A_{\mathrm e,3}(z)=\mathrm e^z~\) , see exp

\(A_{\mathrm e,4}(z)=\mathrm{tet}(z)~\) , see natural tetration

\(A_{\mathrm e,5}(z)=\mathrm{pen}(z)~\) , see natural pentation

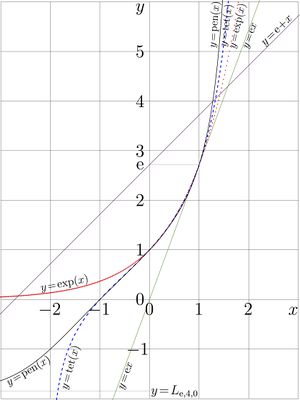
For real values of argument, the first 5 natural ackermanns are shown in figure at right.

Graphics of the natural ackermanns pass though point \((1,\mathrm e)\).

Uniqueness and application

Neither solution of the transfer equation, nor that of the corresponding Abel equation is unique. The additional conditions are required to evaluate the function. .

Since 1950, the holomorphism had been suggested as the important criterion.

It is suggested that asymptotically, each new ackermann approaches the fixed point of the previously considered ackermann. However, this assumes, that the ackermanns are investigated and implemented one by one. As the exponent is already considered and implemented, the tetration can be treated in the similar way, them pentation, and so on.

The real–based ackermanns can be considered as good objects to verify methods of construction of superfunctions and Abel functions. After analysis of various super-exponentials (one of them is 4th ackermann, id est, tetration), the same methods were applied to factorial and to functions, that have sense in the laser science. .

Future work

Holomorphic extension of \(A_{b,m}(z)\), being considered as function of 3 complex variables, \(b\), \(n\), \(z\) may be challenging problem for the future research.

One of possible application of the ackermann functions is denoting of huge numbers. However, the relation between various fast growth functions should be established.

Perhaps, for he applications in physics in century 21, the first four ackernanns are sfficient, id eat, addition, multiplication, exponentiation and tetration. In the similar way, the mulriplication and exponentiation were sufficient for physics in centuries 19 and 20. However, is necessary, the pentation or even more "fast" functions are available.

Ackermanns can be used also as important example for construction of superfunction, for building-up and testing of general methods of evaluation of superfunctions.

References

http://en.citizendium.org/wiki/Ackermann_function

http://en.wikipedia.org/wiki/Ackermann_function

Keywords

Natural tetration, Natural pentation, Pentation, Superfunction, Superfunctions, Tetration, Transfer function

Суперфункции