File:Nembrant.jpg

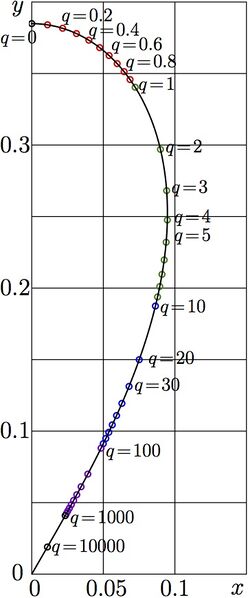
Parametric plot of the function NemBran. It appears as Figure 13.4 at page 162 of book «Superfunctions» ^[1].

NemBran expresses the branchpoint of function ArqNem\(_q\), The imaginary part of the branch point versus the real part for positive values of parameter \(q\):

\(x=\Re(\mathrm{NemBran}(q))\)

\(y=\Im(\mathrm{NemBran}(q))\)

where \(z=\mathrm{NemBran}(q)\) is branchpoint of function \(z\mapsto\mathrm{ArqNem}_q(z)\)

Function NemBran is expressed through function NemBra, that returns solution \(z=\mathrm{NemBra}(q)\) of equation

\(\mathrm{Nem}_q^{\,\prime}(z)=0\)

The representation has the following form:

\(\mathrm{NemBran}(q)=\mathrm{Nem}_q(\mathrm{NemBra}_q(z))\)

While the moguls of the brachpoint is smaller than unity, and the linear term in the representation of the Nemtsov function dominates. For this reason, the parametric plot of function NemBran looks similar to that of function NemBra. I remind the Nemtsov function with parameter \(q\) is defined with

\(\mathrm{Nem}_q(z)=z+z^3+q z^4\)

Position of the branch point returned with function NemBra is the same for all the three versions of the inverse of the Nemtsov function; not only for ArqNem, but also for ArcNem and ArkNem.

Usage

Function NemBran is necessary for evaluation of ArqNem; this function, in its turn, is necessary for expression of the Abel function of the Nemtsov function, denoted with AuNem, in the complex plane.

Function AuNem is described in the updated version of the book Superfunctions as the example of exotic iterate of a transfer function \(T\) such that \(T(0)\!=\!0\) \(T'(0)\!=\!1\) \(T''(0)\!=\!0\).

In such a way, the image Nembrant.jpg had been prepared for the Book Superfunctions ^[1].

One example of such function is \(T=\sin\), bit function sin is symmetric, \(\sin(-z)=-\sin(z)\). Superfunction and Abel Function of sin are denoted with SuSin and AuSin..... The corresponding iterates of sin are reported in 2014 at the Far East Jourmal of Mathematical Science ^[2].

There was interesting to testy the algorithm for some function \(T\) that allows the same exotic iterate but have no symmetry \(T(-z)=-T(z)\). The simplest function of sich a kind is polynomial of 4 order. This polynomial is denoted with term \( \mathrm{Nem}_q \), it is defined at the top. In TORI, this polinomial is called Nemtsov function.

The example with Nemtsov function is important to show, that the symmetry is not essential for the construction of exotic iterates; they can be constructed for asymmetric functions too.

Function Nembran is elementary function; it can be expressed in a closed form. However, this expession is not robust at very small nor at very large values of the argument. For this values, in the code below the two truncated asymptotic expansions are used: Nembra0 and Nembrao.

C++ generator of the plot

#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include <complex>
typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#define DB double
#define DO(x,y) for(x=0;x<y;x++)

void ado(FILE *O, int X, int Y)
{       fprintf(O,"%c!PS-Adobe-2.0 EPSF-2.0\n",'%');
        fprintf(O,"%c%cBoundingBox: 0 0 %d %d\n",'%','%',X,Y);
        fprintf(O,"/M {moveto} bind def\n");
        fprintf(O,"/L {lineto} bind def\n");
        fprintf(O,"/S {stroke} bind def\n");
        fprintf(O,"/s {show newpath} bind def\n");
        fprintf(O,"/C {closepath} bind def\n");
        fprintf(O,"/F {fill} bind def\n");
        fprintf(O,"/o {.002 0 360 arc C S} bind def\n");
        fprintf(O,"/times-Roman findfont 20 scalefont setfont\n");
        fprintf(O,"/W {setlinewidth} bind def\n");
        fprintf(O,"/RGB {setrgbcolor} bind def\n");}
//#include "ado.cin"

z_type nem(DB q,z_type z){ return z*(1.+z*z*(1.+z*q)); }
z_type nem1(DB q,z_type z){ return 1.+z*z*(3.+z*(4.*q)); }
z_type nembra0(DB q){
return -0.5773502691896258*I+ 
        q*(2./9+
        q*(0.2138334330331947*I+
        q*(-0.2633744855967078 +
        q*(-0.3658927631901332*I+
        q*(0.5462581923487273 +
        q*(0.8556857213229570*I+
        q*(-1.387322393266609
        ))))))) ;}

z_type nembrao(DB q){ z_type x,y,z,s; x=conj(pow(z_type(-.25/q,0.),1./3.)); y=x*x; z=y*y;
s=1.+y*(1.+y*(1.+y*(2./3.+z*(-2./3.+y*(-7./9.+z*(11./9.+y*(130./91.)
       )     )     )        )         )         );
return s*x;}

z_type nembra(DB q){
if(fabs(q)<.021) return nembra0(q);
if(fabs(q) >20.) return nembrao(q);
z_type Q,v,V; Q=q*q; v=-1.-8.*Q+4.*sqrt(Q+4.*Q*Q); V=pow(v,1./3.); return (.25/q)*(-1.+1./V+V); }

z_type nembran(DB q){ return nem(q,nembra(q));}

int main(){ int m,n; z_type z,c,d,e; DB x,y,q,u,v;

DO(n,41){ q=-.04+.01*n; c=nembra0(q); d=nem(q,c); e=nem1(q,c); 
printf("%6.3lf %9.5lf %8.5lf %9.5lf %8.5lf %19.15lf %18.15lf\n",q,Re(c),Im(c), Re(d),Im(d), Re(e),Im(e) );}
printf("\n");
DO(n,41){ q=.1*n; c=nembra(q); d=nem(q,c); e=nem1(q,c); 
printf("%6.3lf %9.5lf %8.5lf %9.5lf %8.5lf %19.15lf %18.15lf\n",q,Re(c),Im(c), Re(d),Im(d), Re(e),Im(e) );}
printf("\n");
DO(n,41){ q=1.+1.*n; c=nembrao(q); d=nem(q,c); e=nem1(q,c); 
printf("%6.3lf %9.5lf %8.5lf %9.5lf %8.5lf %19.15lf %18.15lf\n",q,Re(c),Im(c), Re(d),Im(d), Re(e),Im(e) );}

//FILE *o; o=fopen("nembraplo.eps","w"); ado(o,154,604);
FILE *o; o=fopen("nembran.eps","w"); ado(o,154,404);
fprintf(o,"2 2 translate 1000 1000 scale 2 setlinecap\n");
#define M(x,y) fprintf(o,"%8.6f %8.6f M\n",(0.+x),(0.+y));
#define L(x,y) fprintf(o,"%8.6f %8.6f L\n",(0.+x),(0.+y));
#define o(x,y) fprintf(o,"%8.6f %8.6f o\n",(0.+x),(0.+y));

for(n=0;n<41;n+=5){ M(0,.01*n) L(.15,.01*n) }
for(n=0;n<31;n+=5){ M(.01*n,0) L(.01*n,.4) }
fprintf(o,".0006 W S 1 setlinejoin\n");
fprintf(o,"1 0 0 RGB .001 W\n");

for(n= 1;n<10;n++){ q=.1*n; c=nembran(q); x=Re(c); y=-Im(c); o(x,y); }
//for(n=11;n<20;n++){ q=.1*n; c=nembran(q); x=Re(c); y=-Im(c); o(x,y); }
//for(n=21;n<30;n++){ q=.1*n; c=nembran(q); x=Re(c); y=-Im(c); o(x,y); }
fprintf(o,"0 .5 0 RGB\n");
for(n= 1;n<10;n++){ q=1.*n; c=nembran(q); x=Re(c); y=-Im(c); o(x,y); }
fprintf(o,"0 0 1 RGB\n");
for(n= 1;n<10;n++){ q=10.*n; c=nembran(q); x=Re(c); y=-Im(c); o(x,y); }
fprintf(o,".5 0 .8 RGB\n");
for(n= 1;n<10;n++){ q=100.*n; c=nembran(q); x=Re(c); y=-Im(c); o(x,y); }
fprintf(o,"0 0 0 RGB\n");
for(n= 0;n<11;n+=10){ q=100.*n; c=nembran(q); x=Re(c); y=-Im(c); o(x,y); }
                      q=10000.; c=nembran(q); x=Re(c); y=-Im(c); o(x,y); 

for(n= 0;n<400;n++){ q=-.006+.04*(n+.01*n*n+.001*n*n*n); c=nembran(q); x=Re(c); y=-Im(c); if(n==0) M(x,y) else L(x,y); 
printf("%9.3lf %16.6lf %16.6lf\n",q,x,y);
}
L(0,0)
fprintf(o,"0 0 0 RGB .001 W 0 setlinecap S\n");

fprintf(o,"showpage\n%c%cTrailer\n",'%','%');
fclose(o);

system("epstopdf nembran.eps");
system("open     nembran.pdf");
getchar();
return 0;}

Latex generator of labels

\documentclass[12pt]{article}
\usepackage{geometry}
\paperwidth 174pt
\paperheight  420pt
\topmargin -100pt
\oddsidemargin -72pt
\textheight 800px
\parindent 0pt
\usepackage{graphicx}
\usepackage{rotating}
\newcommand \ing {\includegraphics}
\newcommand \sx {\scalebox}
\begin{document}
\begin{picture}(170,410)
%\put(20,14){\ing{nembraplo}}
\put(20,14){\ing{nembran}}
\put(8,411){\sx{1.4}{$y$}}
%\put(0,512){\sx{1.4}{$0.5$}}
%\put(0,412){\sx{1.4}{$0.4$}}
\put(0,312){\sx{1.4}{$0.3$}}
\put(0,212){\sx{1.4}{$0.2$}}
\put(0,112){\sx{1.4}{$0.1$}}
\put(8,12){\sx{1.4}{$0$}}
\put(20,1){\sx{1.4}{$0$}}
\put(60,1){\sx{1.4}{$0.05$}}
\put(112,1){\sx{1.4}{$0.1$}}
\put(162,2){\sx{1.4}{$x$}}
%\put(18,601){\sx{1.1}{$q\!=\!0$}}
\put(0,389){\sx{1.1}{$q\!=\!0$}}
%\put(63,593){\sx{1.1}{$q\!=\!0.2$}}
\put(43,404){\sx{1.1}{$q\!=\!0.2$}}
%\put(97,574){\sx{1.1}{$q\!=\!0.4$}}
\put(62,394){\sx{1.1}{$q\!=\!0.4$}}
\put(78,384){\sx{1.1}{$q\!=\!0.6$}}
\put(88,372){\sx{1.1}{$q\!=\!0.8$}}
\put(97,356){\sx{1.1}{$q\!=\!1$}}
\put(116,312){\sx{1.1}{$q\!=\!2$}}
\put(120,284){\sx{1.1}{$q\!=\!3$}}
\put(122,263){\sx{1.1}{$q\!=\!4$}}
\put(122,250){\sx{1.1}{$q\!=\!5$}}
\put(112,200){\sx{1.1}{$q\!=\!10$}}
\put(104,164){\sx{1.1}{$q\!=\!20$}}
\put(94,145){\sx{1.1}{$q\!=\!30$}}
\put( 74,99){\sx{1.1}{$q\!=\!100$}}
\put( 49,52){\sx{1.1}{$q\!=\!1000$}}
\put( 36,32){\sx{1.1}{$q\!=\!10000$}}
\end{picture}
\end{document}

References

Keywords

«ArqNem», «AuNem», «Book», «Branch point», «C++», «Latex», «NemBra», «NemBran», «Nemtsov function», «SuNem», «AuNem», «Parametric plot»,