Difference between revisions of "Iterate of exponential"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| (34 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [[File:ExpIte4T.jpg| |
+ | [[File:ExpIte4T.jpg|280px|left|thumb|\(y=\exp^n(x)~\) versus real \(x\) for various \(n\)]] |
| − | [[File:Exp1mapT200.jpg| |
+ | [[File:Exp1mapT200.jpg|280px|thumb|\(u\!+\!\mathrm i v=\exp^1(x\!+\!\mathrm i y)=\exp(x\!+\!\mathrm i y)\)]] |
| − | [[File:Exp09mapT200.jpg| |
+ | [[File:Exp09mapT200.jpg|280px|thumb|\(u+\mathrm i v=\exp^{0.9}(x+\mathrm i y)\)]] |
| − | [[File:Exp05mapT200.jpg| |
+ | [[File:Exp05mapT200.jpg|280px|thumb|\(u+\mathrm i v=\exp^{0.5}(x+\mathrm i y)\)]] |
| + | [[File:Exp01mapT200.jpg|280px|thumb|\(u+\mathrm i v=\exp^{0.1}(x+\mathrm i y)\)]] |
||
| ⚫ | |||
| + | [[File:Exm01mapT200.jpg|280px|thumb|\(u+\mathrm i v=\exp^{-0.1}(x+\mathrm i y)=\ln^{0.1}(x+\mathrm i y)\)]] |
||
| + | [[File:Exm05mapT200.jpg|280px|thumb|\(u+\mathrm i v=\exp^{-0.5}(x+\mathrm i y)=\ln^{0.5}(x+\mathrm i y)\)]] |
||
| + | [[File:Exm09mapT200.jpg|280px|thumb|\(u+\mathrm i v=\exp^{-0.9}(x+\mathrm i y)=\ln^{0.9}(x+\mathrm i y)\)]] |
||
| + | [[File:Exm1mapT200.jpg|280px|thumb|\(u+\mathrm i v=\exp^{-1}(x+\mathrm i y)=\ln(x+\mathrm i y)\)]] |
||
| ⚫ | |||
In [[TORI]], the number in superscript after a name of any function denotes the number of iteration. This notation is neither new, nor original; |
In [[TORI]], the number in superscript after a name of any function denotes the number of iteration. This notation is neither new, nor original; |
||
| Line 12: | Line 17: | ||
</ref>. |
</ref>. |
||
| + | ==Integer and non-integer \(n\)== |
||
| ⚫ | |||
| + | <!-- |
||
| ⚫ | |||
| − | The most often are the first iteration of exponent, |
+ | The most often are the first iteration of exponent, \(n=1\); \(\exp^1=\exp\) |
| − | and the minus first iteration, |
+ | and the minus first iteration, \(n=-1\); \(\exp^{-1} = \ln\). |
| − | Less often they appear with |
+ | Less often they appear with \(n = \pm 2\); \(\exp^2(z)=\exp(\exp(z))\), and \(\exp^{-2}(z)=\ln(\ln(z))\). |
| − | Other values of number of iteration are not usual, and until 2008, there was no regular way to evaluate iteration of exponential for any non–integer number |
+ | Other values of number of iteration are not usual, and until year 2008, there was no regular way to evaluate iteration of exponential for any non–integer number \(n\) of iteration. |
| − | However, with [[tetration]] tet, that is [[superfunction]] of [[exponent]], and [[Arctetration]] ate, that is [[Abel function]] of exponent, the |
+ | However, with [[tetration]] tet, that is [[superfunction]] of [[exponent]], and [[Arctetration]] ate, that is [[Abel function]] of exponent, the \(n\)th iteration can be expressed as follows: |
| − | + | \(\exp^n(z)=\mathrm{tet}(n+\mathrm{ate}(z))\) |
|
| + | Both, tet and ate are holomorphic functions; so, the representation above can be used for non-integer \(n\). The exponential can be iterated even complex number of times. |
||
| ⚫ | |||
| + | |||
| + | ==Iimplementation== |
||
| + | |||
| ⚫ | |||
Methods for the evaluation are described in 2009 by D.Kouznetsov in [[Mathematics of Computation]] |
Methods for the evaluation are described in 2009 by D.Kouznetsov in [[Mathematics of Computation]] |
||
<ref> |
<ref> |
||
| Line 30: | Line 41: | ||
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf<br> |
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf<br> |
||
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf |
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf |
||
| − | D. Kouznetsov. Solution of |
+ | D. Kouznetsov. Solution of \(F(x+1)=\exp(F(x))\) in complex \(z\)-plane. 78, (2009), 1647-1670 |
| − | </ref>, and the efficient [[C++]] complex double implementation are described in 2010 in [[ |
+ | </ref>, and the efficient [[C++]] complex double implementation are described in 2010 in [[Vladikavkaz mathematical Journal]] in Russian; the English version is also loaded |
<ref> |
<ref> |
||
http://www.ils.uec.ac.jp.jp/~dima/PAPERS/2009vladie.pdf (English) <br> |
http://www.ils.uec.ac.jp.jp/~dima/PAPERS/2009vladie.pdf (English) <br> |
||
| Line 37: | Line 48: | ||
http://mizugadro.mydns.jp/PAPERS/2009vladir.pdf (Russian version) <br> |
http://mizugadro.mydns.jp/PAPERS/2009vladir.pdf (Russian version) <br> |
||
D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45. |
D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45. |
||
| + | </ref>. WIth known properties and the efficient implementation, functions tet, ate and non–integer ietrations of the exponent shouls be qualified as [[special function]]s; in computation, one can access them as if they would be elementary functions. |
||
| ⚫ | |||
| + | The [[complex doube]] implementations of functions tet and ate are loaded to [[TORI]], see [[fsexp.cin]] and [[fslog.cin]]; they run at various operational systems; at least under Linux and Macintosh. Reports of any problems with the use or the reproducible bugs should be appreciated. |
||
| ⚫ | |||
| − | </ref>. |
||
| ⚫ | |||
| − | |||
| ⚫ | |||
| ⚫ | |||
and |
and |
||
| + | lines \(v=\Im(f)\) for various values \(n\) in the \(x\),\(y\) plane. As the function is real-holomorphic, the maps are symmetric; so the only upper half plane is shown in the figures. |
||
| − | lines $v=\Im(f(x+\mathrm i y))$ for various values $n$. |
||
| + | |||
| + | ==Cut lines== |
||
| + | While \(n\) is not integer, \(\exp^n(z)\) is holomorphic in the complex plane with two cut lines \(\Re(z)\le \Re(L)\), \(\Im(z)=\pm \Im(L)\), where |
||
| + | \(L\approx 0.3+1.3 \mathrm i\) is [[fixed point]] of [[logarithm]], id est, solution of equation |
||
| + | |||
| + | \(L=\ln(L)\). |
||
| + | |||
| + | In the figures at right, one of these cuts is seen; it is marked with dashed line. |
||
| + | The additional levels \(\Re(L)\) for the real part of \(\exp^n\) and \(\Im(L)\) for the imaginary part are drown with thick green lines; of course, these lines cross each other at the branch point \(L\). |
||
| + | |||
| + | In addition, for negative number \(n\) of iterations (and, in particular, for \(n=-1\)), there is cut line along the negative part of the real axis, id est, from \(-\infty\) to \(\mathrm{tet}(-2-n)\). |
||
| + | |||
| + | ==Special function== |
||
| + | Properties of the iteration of the exponential are described. |
||
| + | |||
| + | \(\exp^n(z)\) is holomorphic function with respect to \(z\) and with respect to \(n\). |
||
| + | Properties of this function are analyzed and described. |
||
| + | The efficient (fast and precise) algorithm for the evaluation is supplied with routines [[fsexp.cin]] and [[cslog.cin]]. |
||
| + | |||
| + | With achievements above, function \((n,z) \mapsto \exp^n(z)\) is qualified as [[special function]]. Designers of compilers and interpreters from the programming languages are invited to borrow the implementations of [[tetration]] and [[arctetration]] in order to provide the built-in function, that evaluates \(\exp^n(z)\) for complex values of \(n\) and \(z\). In particular, in Mathematica, there is already name for such a function; it should be called with Nest[Exp,z,n]. Up to year 2013, the built-in function [[Nest]] is implemented in such a way, that number \(n\) of iteration should be expressed with natural constant, positive integer number |
||
| ⚫ | |||
| + | http://reference.wolfram.com/mathematica/ref/Nest.html |
||
| + | Nest, Wolfram Mathematica 9 Documentation center, 2013. |
||
| + | </ref>. Over-vice, the built-in function generates the error message instead of to perform the calculations and evaluations requested. With use of [[superfunction]]s and [[Abel function]]s, Nest could be implemented for more general case. |
||
==References== |
==References== |
||
<references/> |
<references/> |
||
| + | <!-- |
||
http://www.ams.org/journals/bull/1993-29-02/S0273-0979-1993-00432-4/S0273-0979-1993-00432-4.pdf |
http://www.ams.org/journals/bull/1993-29-02/S0273-0979-1993-00432-4/S0273-0979-1993-00432-4.pdf |
||
Walter Bergweiler. Iteration of meromorphic functions. Bull. Amer. Math. Soc. 29 (1993), 151-188. |
Walter Bergweiler. Iteration of meromorphic functions. Bull. Amer. Math. Soc. 29 (1993), 151-188. |
||
| Line 55: | Line 90: | ||
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf<br> |
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf<br> |
||
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf |
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf |
||
| − | D. Kouznetsov. Solution of |
+ | D. Kouznetsov. Solution of \(F(x+1)=\exp(F(x))\) in complex \(z\)-plane. 78, (2009), 1647-1670 |
| + | !--> |
||
==Keywords== |
==Keywords== |
||
| Line 63: | Line 99: | ||
[[Exponent]], |
[[Exponent]], |
||
[[Iteration]], |
[[Iteration]], |
||
| + | [[Logarithm]], |
||
[[Superfunction]], |
[[Superfunction]], |
||
| + | [[Superfunctions]], |
||
[[Tetration]], |
[[Tetration]], |
||
| − | [[Category:Abel function]] |
+ | [[Category:Abel function]] |
| − | [[Category:Arctetration]] |
+ | [[Category:Arctetration]] |
| − | [[Category:Exponent]] |
+ | [[Category:Exponent]] |
[[Category:English]] |
[[Category:English]] |
||
| − | [[Category:Iteration]] |
+ | [[Category:Iteration]] |
| − | [[Category: |
+ | [[Category:Iteration of exp]] |
| − | [[Category: |
+ | [[Category:Logarithm]] |
| + | [[Category:Superfunction]] |
||
| + | [[Category:Superfunctions]] |
||
| + | [[Category:Tetration]] |
||
Latest revision as of 18:43, 30 July 2019
Iteration of exponential (or Iteration of exponent) is function \(f(z)=\exp^n(z)\), where upper superscript indicates the number of iteration.
In TORI, the number in superscript after a name of any function denotes the number of iteration. This notation is neither new, nor original; Walter Bergweiler had used it in century 20 [1].
Integer and non-integer \(n\)
The most often are the first iteration of exponent, \(n=1\); \(\exp^1=\exp\)
and the minus first iteration, \(n=-1\); \(\exp^{-1} = \ln\).
Less often they appear with \(n = \pm 2\); \(\exp^2(z)=\exp(\exp(z))\), and \(\exp^{-2}(z)=\ln(\ln(z))\). Other values of number of iteration are not usual, and until year 2008, there was no regular way to evaluate iteration of exponential for any non–integer number \(n\) of iteration. However, with tetration tet, that is superfunction of exponent, and Arctetration ate, that is Abel function of exponent, the \(n\)th iteration can be expressed as follows:
\(\exp^n(z)=\mathrm{tet}(n+\mathrm{ate}(z))\)
Both, tet and ate are holomorphic functions; so, the representation above can be used for non-integer \(n\). The exponential can be iterated even complex number of times.
Iimplementation
Representation of \(\exp^n\) through function tet and ate defines the \(n\)th iterate of exponential for any complex number \(n\) of iterations. Methods for the evaluation are described in 2009 by D.Kouznetsov in Mathematics of Computation [2], and the efficient C++ complex double implementation are described in 2010 in Vladikavkaz mathematical Journal in Russian; the English version is also loaded [3]. WIth known properties and the efficient implementation, functions tet, ate and non–integer ietrations of the exponent shouls be qualified as special functions; in computation, one can access them as if they would be elementary functions. The complex doube implementations of functions tet and ate are loaded to TORI, see fsexp.cin and fslog.cin; they run at various operational systems; at least under Linux and Macintosh. Reports of any problems with the use or the reproducible bugs should be appreciated.
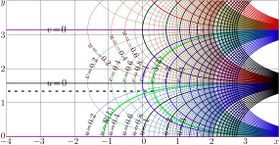
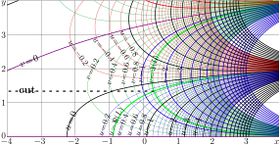
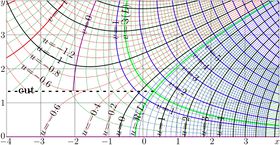
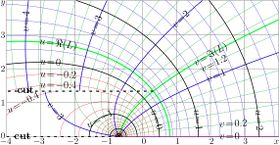
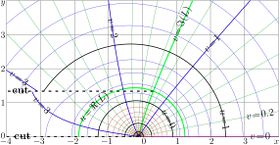
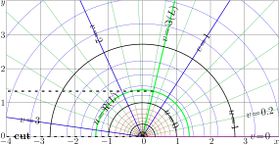
Complex maps of the \(n\)th iteration of exponential, \(f=\exp^n(x+\mathrm i y)\) are shown in figures at right with lines \(u=\Re(f)\) and lines \(v=\Im(f)\) for various values \(n\) in the \(x\),\(y\) plane. As the function is real-holomorphic, the maps are symmetric; so the only upper half plane is shown in the figures.
Cut lines
While \(n\) is not integer, \(\exp^n(z)\) is holomorphic in the complex plane with two cut lines \(\Re(z)\le \Re(L)\), \(\Im(z)=\pm \Im(L)\), where \(L\approx 0.3+1.3 \mathrm i\) is fixed point of logarithm, id est, solution of equation
\(L=\ln(L)\).
In the figures at right, one of these cuts is seen; it is marked with dashed line. The additional levels \(\Re(L)\) for the real part of \(\exp^n\) and \(\Im(L)\) for the imaginary part are drown with thick green lines; of course, these lines cross each other at the branch point \(L\).
In addition, for negative number \(n\) of iterations (and, in particular, for \(n=-1\)), there is cut line along the negative part of the real axis, id est, from \(-\infty\) to \(\mathrm{tet}(-2-n)\).
Special function
Properties of the iteration of the exponential are described.
\(\exp^n(z)\) is holomorphic function with respect to \(z\) and with respect to \(n\). Properties of this function are analyzed and described. The efficient (fast and precise) algorithm for the evaluation is supplied with routines fsexp.cin and cslog.cin.
With achievements above, function \((n,z) \mapsto \exp^n(z)\) is qualified as special function. Designers of compilers and interpreters from the programming languages are invited to borrow the implementations of tetration and arctetration in order to provide the built-in function, that evaluates \(\exp^n(z)\) for complex values of \(n\) and \(z\). In particular, in Mathematica, there is already name for such a function; it should be called with Nest[Exp,z,n]. Up to year 2013, the built-in function Nest is implemented in such a way, that number \(n\) of iteration should be expressed with natural constant, positive integer number [4]. Over-vice, the built-in function generates the error message instead of to perform the calculations and evaluations requested. With use of superfunctions and Abel functions, Nest could be implemented for more general case.
References
- ↑ http://www.ams.org/journals/bull/1993-29-02/S0273-0979-1993-00432-4/S0273-0979-1993-00432-4.pdf Walter Bergweiler. Iteration of meromorphic functions. Bull. Amer. Math. Soc. 29 (1993), 151-188.
- ↑
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf D. Kouznetsov. Solution of \(F(x+1)=\exp(F(x))\) in complex \(z\)-plane. 78, (2009), 1647-1670 - ↑
http://www.ils.uec.ac.jp.jp/~dima/PAPERS/2009vladie.pdf (English)
http://mizugadro.mydns.jp/PAPERS/2010vladie.pdf (English)
http://mizugadro.mydns.jp/PAPERS/2009vladir.pdf (Russian version)
D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45. - ↑ http://reference.wolfram.com/mathematica/ref/Nest.html Nest, Wolfram Mathematica 9 Documentation center, 2013.
Keywords
Abel function, Arctetration, Exponent, Iteration, Logarithm, Superfunction, Superfunctions, Tetration,