Iterate of exponential

$y=\exp^n(x)~$ versus real $x$ for various $n$

$u\!+\!\mathrm i v=\exp^1(x\!+\!\mathrm i y)=\exp(x\!+\!\mathrm i y)$

$u+\mathrm i v=\exp^{0.9}(x+\mathrm i y)$

$u+\mathrm i v=\exp^{0.5}(x+\mathrm i y)$

$u+\mathrm i v=\exp^{0.1}(x+\mathrm i y)$

$u+\mathrm i v=\exp^{-0.1}(x+\mathrm i y)=\ln^{0.1}(x+\mathrm i y)$

$u+\mathrm i v=\exp^{-0.5}(x+\mathrm i y)=\ln^{0.5}(x+\mathrm i y)$

$u+\mathrm i v=\exp^{-0.9}(x+\mathrm i y)=\ln^{0.9}(x+\mathrm i y)$

$u+\mathrm i v=\exp^{-1}(x+\mathrm i y)=\ln(x+\mathrm i y)$

Iteration of exponential (or Iteration of exponent) is function $f(z)=\exp^n(z)$, where upper superscript indicates the number of iteration.

In TORI, the number in superscript after a name of any function denotes the number of iteration. This notation is neither new, nor original; Walter Bergweiler had used it in century 20 .

Integer and non-integer $n$

The most often are the first iteration of exponent, $n=1$; $\exp^1=\exp$

and the minus first iteration, $n=-1$; $\exp^{-1} = \ln$.

Less often they appear with $n = \pm 2$; $\exp^2(z)=\exp(\exp(z))$, and $\exp^{-2}(z)=\ln(\ln(z))$. Other values of number of iteration are not usual, and until year 2008, there was no regular way to evaluate iteration of exponential for any non–integer number $n$ of iteration. However, with tetration tet, that is superfunction of exponent, and Arctetration ate, that is Abel function of exponent, the $n$th iteration can be expressed as follows:

$\exp^n(z)=\mathrm{tet}(n+\mathrm{ate}(z))$

Iimplementation

Representation of $\exp^n$ through function tet and ate defines the $n$th iterate of exponential for any complex number $n$ of iterations. Methods for the evaluation are described in 2009 by D.Kouznetsov in Mathematics of Computation , and the efficient C++ complex double implementation are described in 2010 in Vladikavkaz mathematical Journal in Russian; the English version is also loaded . WIth known properties and the efficient implementation, functions tet, ate and non–integer ietrations of the exponent shouls be qualified as special functions; in computation, one can access them as if they would be elementary functions. The complex doube implementations of functions tet and ate are loaded to TORI, see fsexp.cin and fslog.cin; they run at various operational systems; at least under Linux and Macintosh. Reports of any problems with the use or the reproducible bugs should be appreciated.

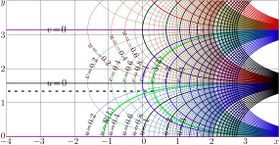
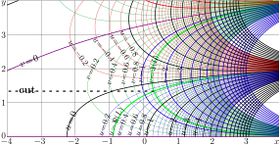
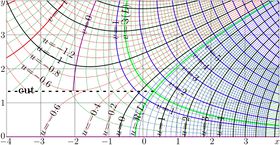
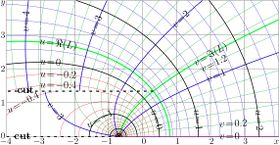
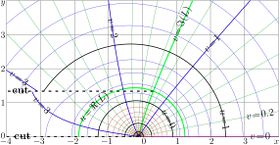
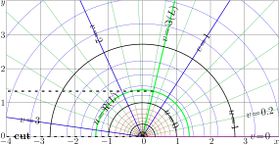
Complex maps of the $n$th iteration of exponential, $f=\exp^n(x+\mathrm i y)$ are shown in figures at right with lines $u=\Re(f)$ and lines $v=\Im(f)$ for various values $n$ in the $x$,$y$ plane. As the function is real-holomorphic, the maps are symmetric; so the only upper half plane is shown in the figures.

Cut lines

While $n$ is not integer, $\exp^n(z)$ is holomorphic in the complex plane with two cut lines $\Re(z)\le \Re(L)$, $\Im(z)=\pm \Im(L)$, where $L\approx 0.3+1.3 \mathrm i$ is fixed point of logarithm, id est, solution of equation

$L=\ln(L)$.

In the figures at right, one of these cuts is seen; it is marked with dashed line. The additional levels $\Re(L)$ for the real part of $\exp^n$ and $\Im(L)$ for the imaginary part are drown with thick green lines; of course, these lines cross each other at the branch point $L$.

In addition, for negative number $n$ of iterations (and, in particular, for $n=-1$), there is cut line along the negative part of the real axis, id est, from $-\infty$ to $\mathrm{tet}(-2-n)$.

Special function

Properties of the iteration of the exponential are described.

$\exp^n(z)$ is holomorphic function with respect to $z$ and with respect to $n$. Properties of this function are analyzed and described. The efficient (fast and precise) algorithm for the evaluation is supplied with routines fsexp.cin and cslog.cin.

With achievements above, function $(n,z) \mapsto \exp^n(z)$ is qualified as special function. Designers of compilers and interpreters from the programming languages are invited to borrow the implementations of tetration and arctetration in order to provide the built-in function, that evaluates $\exp^n(z)$ for complex values of $n$ and $z$. In particular, in Mathematica, there is already name for such a function; it should be called with Nest[Exp,z,n]. Up to year 2013, the built-in function Nest is implemented in such a way, that number $n$ of iteration should be expressed with natural constant, positive integer number . Over-vice, the built-in function generates the error message instead of to perform the calculations and evaluations requested. With use of superfuncitons and Abel functions, Nest could be implemented for more general case.

Keywords

Abel function, Arctetration, Exponent, Iteration, Logarithm, Superfunction, Tetration,