Kori
kori function appears in the calculus of the loss in the pinhole waveguide in the paraxial approximation.
The integrand for the overlapping of the Bessel mode to the propagated Bessel mode is expressed through function kori.
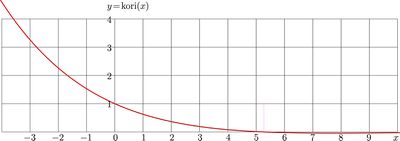
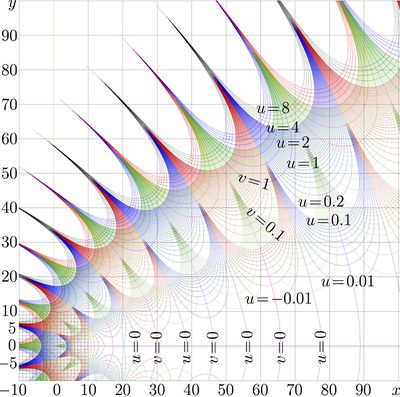
Explicit plot and complex map of function kori are shown in figures at right.
Contents
Definition
For \(z\ne 1~\), \(~ ~\mathrm{kori}(z)=\displaystyle \frac{J_0\big(L\, \sqrt{x}\big)}{1-z}\)
where \(L=\,\) BesselJZero\([0,1]\approx 2.4048255576957727686\)
At unity, kori is defined as the corresponding limit, id est,
\(\mathrm{kori}(1)=\,\) \(\displaystyle \lim_{z\rightarrow 1} \, \mathrm{kori}(z)=\,\) \( \displaystyle \frac{L}{2} J_1(L)\approx 0.624229584847753325\)
For real values of the argument, the explicit plot go function kori is shown in figure at top.
Properties
Kori is entire function, it is holomorphic in the whole complex plane. The zero in the denominator in the definition is compensated with the first zero of the Bessel function. In the similar way, the branch cut line of the square root in the argument is compensated by the symmetry of the Bessel function, \(J_0(-z)=J_0(z)\)/
For real values of the argument, kori grows to infinity at minus infinity. At the increasing of the argument, kori decreases, take value 1 at zero, and becomes zero at
\((\mathrm{BesseljZero}[0,2]/\mathrm{BesseljZero}[0,1])^2 \approx 5.268940431605222\)
At the graphic, the corresponding abscissa is marked with thin pink vertical line.
At larger value of the argument, kori continue decreasing until its absolute minimum approximately
\(-0.042157174825374066\) at value of argument approximately \(7.744892003497505\), and then continues oscillations in vicinity of zero, with increasing distance between zeros and decreasing amplitude.
First zeros of function kori are:
\(M_2=(L_2/L_1)^2 \approx ~ ~ ~ 5.268940431605222\)
\(M_3=(L_3/L_1)^2 \approx ~ 12.949091948711432\)
\(M_4=(L_4/L_1)^2 \approx ~ 24.042160379641807\)
\(M_5=(L_5/L_1)^2 \approx ~ 38.54835466920391\)
\(M_6=(L_6/L_1)^2 \approx ~ 56.467724715172444\)
\(M_7=(L_7/L_1)^2 \approx ~ 77.80028714289774\)
\(M_8=(L_8/L_1)^2 \approx\! 102.54604874469128\)
\(M_9=(L_9/L_1)^2 \approx\! 130.70501270873422\)
where \(L_n=\mathrm{BesselJZero}(0,n)\) is \(n\)th zero of the Bessel function BesselJ0.
Norm of kori
\(\displaystyle \int_0^\infty \mathrm{kori}(x)^2 \,\mathrm d x = 1\)
Expansion at zero
As kori is entire function, the Taylor series absolutely converge at any value of the argument. In particular, the expansion at zero can be written as follows:
\(\mathrm{kori}(x) \displaystyle =1+\sum_{n=1}^{\infty} c_n x^n\)
The first coefficients \(c\) are:
\(c_1= 1-\frac{L^2}{4} \approx - 0.44579649073669613\)
\(c_2= 1-\frac{L^2}{4}+\frac{L^4}{64}\approx 0.07678538241994023\)
\(c_3= 1-\frac{L^2}{4}+\frac{L^4}{64}-\frac{L^6}{2304}\approx -0.007164288505890223\)
\(c_4= 1-\frac{L^2}{4}+\frac{L^4}{64}-\frac{L^6}{2304}+\frac{L^8}{147456}\approx 0.000421595220551409\)
\(c_5= 1-\frac{L^2}{4}+\frac{L^4}{64}-\frac{L^6}{2304}+\frac{L^8}{147456}-\frac{L^{10}}{14745600}\approx -0.00001711054228162748\)
In order to get accurate estimate of these coefficients, the high precision arithmetics is required, because the summations in the expressions above begin with terms of order of unity and, for high number of coefficients, end with small term, leading to even smaller amounts.
Expansion at Infinity

For large values of the argument, the asymptotic expansion of kori can be written in terms of amplitude and phase, in analogy with that of function BesselJ0:
\(\displaystyle \mathrm{kori}(x) = - \sqrt{\frac{2}{\pi L_1}} x^{-5/4} \, G(x)\, \cos\left( - \frac{\pi}{4} + L_1 \sqrt{x}\, F(x) \right) \)
where
\(F(x) = 1 \) \(\displaystyle - \frac{1}{8\, L_1^2 x} \) \(\displaystyle +\frac{25}{384\, (L_1^2 x)^2}\) \(\displaystyle - \frac{1073}{5120\, (L_1^2 x)^3} \) \(\displaystyle + \frac{375733}{229376\, (L_1^2 x)^4} \) \(\displaystyle - \frac{55384775}{2359296\, (L_1^2 x)^5} \) \(\displaystyle +..\) \( = \displaystyle \sum_{n=0}^{N-1} f_n x^{-n} +O(x^{-N}) \)
\(\displaystyle G(x) = 1 + \left(1-\frac{1}{16\, L_1^2}\right) \frac{1}{x} \) \( + \left(1-\frac{1}{16\, L_1^2} + \frac{53}{512\, L_1^4}\right) \frac{1}{x^2} + .. \) \( = \displaystyle \sum_{n=0}^{N-1} g_n x^{-n} +O(x^{-N})\)
The asymptotic approximation korias can be written as follows:
\(\displaystyle
\mathrm{korias}_m(x) = - \sqrt{\frac{2}{\pi L_1}} x^{-5/4} \, G_m(x)\,
\cos\left( - \frac{\pi}{4} + L_1 \sqrt{x}\, F_m(x) \right)
\)
where
\(G_m(x) = \sum_{n=0}^{m} g_n x^{-n}\)
\(F_m(x) = \sum_{n=0}^{m} f_n x^{-n}\)
Complex map of this approximation for \(m=11\) is shown in figure at right; it is almost the same as map of function kori; significant deviation is seen only for argument of order of few units in vicinity of zero (it appears as white spot); so, only this part of the map is shown.
Approximations for the coefficients \(f\) and \(g\) are:
\(\begin{array}{l} f_0=1\\ f_1=- 0.021614383628830615865\\ f_2=0.0019465899152260872595\\ f_3=-0.0010834984344719114778\\ f_4=0.001464410164512283719\\ f_5=-0.003628876399615993660\\ f_6=0.01431760830195380729\\ f_7=-0.0824438982874790057\\ f_8=0.652747801052423657\\ f_9=-6.80376838070624330\\ f_{10}=90.322658904953727\\ f_{11}=-1487.942880868968812\\ f_{12}=29785.50901270392374\\ \end{array}\) \(~\) \(\begin{array}{l} g_0=1 \\ g_1=0.989192808185584692068 \\ g_2=0.99228788615079417081 \\ g_3= 0.989481317221334367489\\ g_4= 0.994709980602617872387\\ g_5= 0.97818700495778240956\\ g_6=1.0575251177784290263\\ g_7= 0.5188843197279991625\\ g_8=5.432808917007474985\\ g_9=-52.5640507009104629\\ g_{10}=807.429675670594971\\ g_{11}= -14844.4023379433794\\ g_{12}=328204.367306340176 \end{array}\)
Approximations for the 12+12 coefficients are copypasted above in order to show their growth. For evaluation of kori with 14 decimal digits, it may have sense to cut the series at 6th or at 7th term; then, the truncated series provide good estimate of \(\mathrm{kori}(z)\) for \(|z|>30\). In vicinity of the boundary of this region, the increase of number of terms do not improve the precision of the evaluation.
Approximation for interval from 0 to \((L_2/L_1)^2\)

For the application, the interval between \(~0~\) and \(~(L_2/L_1)^2\approx 5.268940431605222~ \) is especially important. In this range kori can be approximated with the polynomial below:
\(\mathrm{korifit}[x]=\displaystyle \left( 1- \Big(\frac{L_1}{L_2}\Big)^2 x\right) \) \(\displaystyle \left( 1- \Big(\frac{L_1}{L_3}\Big)^2 x\right)\) \(\displaystyle \left(1+\sum_{n=1}^{15} c_n x^n\right)\)
with the following array of coefficients (numeration begins with 0):
c[16]={1,
-0.256005011219941993570670508019,
0.0281978125768042007057113441199,
-0.00181258393780241662780680613867,
0.0000775822332475845672943781286224,
-2.38609544935449493722623606533e-6,
5.5465254159392191445565645766e-8,
-1.01054597146460752951273870914e-9,
1.48348772753372628782330712313e-11,
-1.79332434839872451210764178471e-13,
1.81697031752603393402790223753e-15,
-1.56569115453044785387543614077e-17,
1.16170076283001586118141461154e-19,
-7.50065787627627390138399503073e-22,
4.25298321710799220467323756624e-24,
-2.13477668517290665487301104539e-26};
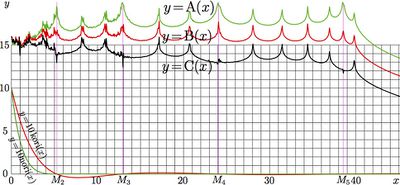
In the specified range, this approximation provides of order of 15 significant figures, and in this range it is better than the naive, direct implementation by definition through the C++ built-in function double j0(double). Especially poor the naive implementation is in vicinity of zero. The deviation, scaled with factor \(10^{15}\), is shown in figure above.
Several tens of similar coefficients can be evaluated, extending the sum above and improving the expansion.
korifit76
For real values of the argument, and also, for moderate values of the imaginary part of the argument, the approximation korifit76 is suggested:
\(\mathrm{kori}(x) \approx \mathrm{kori76fit}(x)= \prod_{n=2}^7\! \left(1\!-\!M_n x\right)~ \frac{1+\sum_{n=1}^6 a_n x^n}{1+\sum_{n=1}^6 b_n x^n} \)
where coefficients \(a\) and \(b\) are:
\(\begin{array}{l} a_1=-0.04844698269548584 \\ a_2= 0.0010028289633265202 \\ a_3= -0.000011428855401098336\\ a_4= 7.61813379974462\times 10^{-8}\\ a_5= -2.8376606186641804\!\times\! 10^{-10}~\\ a_6= 4.651275051439759\times 10^{-13} \end{array}\) \(\begin{array}{l} b_1= 0.03223483760044156\\ b_2= 0.0004974915308429358\\ b_3= 4.7768603073237505\times 10^{-6}\\ b_4= 3.071615607112112\times 10^{-8}\\ b_5= 1.292095753771865\times 10^{-10}\\ b_6= 2.925186494186955\times 10^{-13} \end{array} \)
This approximation is valid, roughly, for \(-1\!<\!\Re(x)\!<\! 40\) and \(|\Im(z)|<2\), providing several significant figures in this range.
In order to indicate the precision and the range of validity of approximation korifit76 for real argument, the figure at right shows agreements
\(\mathrm{A}(x)= \) \(- \lg\! \Big( \big|\mathrm{korifit76}(x)^2-\mathrm{kori}^2(x)\big|\Big)\)
\(\mathrm{B}(x)= \) \(- \lg\! \Big( \big|\mathrm{korifit76}(x)-\mathrm{kori}(x)\big| \Big)\)
\(\displaystyle \mathrm{C}(x)\!=\!\) \(\displaystyle - \lg \left(\!\frac {\big|\mathrm{korifit76}(x)-\mathrm{kori}(x)\big|}{\big|\mathrm{korifit76}(x)\big| \!+\! \big|\mathrm{kori}(x)\big|}\right)\)
The additional vertical lines in the plot at right indicates zeros of function korifit76; they are defined with
\(M_n=(L_n/L_1)^2\) for \(n=2\, ..\, 5\); they coincide with zeros the approximated function.
At the bottom, the approximated function and its square are shown, scaled with factor 10, id est,
\(y=10\,\mathrm{kori}(x)\) and
\(y=10\,\mathrm{nori}(x)=10\,\mathrm{kori}(x)^2\),
Roughly, the agreements indicate, how many correct decimal digits can be achieved at the use of korifit76 instead of function kori.
The upper curve, \(y=\mathrm{A}(x)\), shows, that at the integration of square of this approximation from zero to at least 42 with a complex exponent, the errors of fitting do not make the precision worse, as it is determined by the precision of evaluation of function in vicinity of zero (where it is of order of unity. This estimate is important for approximation and numerical implementation of function naga,
naga\((x)=\int_0^\infty \mathrm{kori}(p)^2 \exp(\mathrm i \, p \, x) \, \mathrm d x\)
In the complex plane, the range of function nori is roughly, the ellipse, that extends from \(-1\) to \(40\) by the along the real part, and from \(-2\) to \(2\) along the imaginary part.
Application
Function kori appears in the expression for the loss of the principal Bessel mode in the pinhole waveguide. In such a way, the description and implementation of functions kori and some other related functions (maga, mori, naga, nori) appear as tools for the description of waves in such a waveguide, following the general concepts and ideology of TORI.
For real \(p\), this loss in the pinhole waveguide is estimated as
maga\((p )=1- \displaystyle {\left|\int_0^\infty \mathrm{kori}(x)^2\, \exp(\mathrm i p x) \, \mathrm d x\right|}^{~ ~ 2}\)
Here, argument \(p\) has the following physical sense:
\(\displaystyle p= \frac{T}{2 k} \left(\frac{L_1}{r}\right)^2\)
where \(k\) is wavenumber, \(r\) is radius of the pinholes, and \(T\) is distance between the pinholes. Then, function maga gives the first approximation in the loss of the Bessel mode in such a waveguide, in the limit of small \(p\).
The expression for maga allows the holomorphic extension for the complex \(p\);
maga\((p )=1- \displaystyle \lim_{A\rightarrow \infty} \Bigg( \) \(\displaystyle \left(\int_0^A\mathrm{kori}(x)^2\, \cos(p x) \, \mathrm d x\right)^2 + \) \(\displaystyle \left(\int_0^A \mathrm{kori}(x)^2\, \sin(p x) \, \mathrm d x\right)^2 \Bigg)\)
The straightforward numerical integration in these expressions happened to be non-efficient, even for real \(p\); for this reason, the analytical properties of the integrand, and, in particular, those of function kori, deserve the detailed investigation, analysis and description.
One of goal is to calculate the asymptotic expansion of function maga at small values of its argument, (\(\,|p|\!\ll\! 1\,\)), at large values of its argument (\(\,|p|\!\gg\! 1\,\)), to check agreement between the approximations based on these expansions and to generate the complex map of function maga. For this goal, the fast and precise implementation of function kori is necessary. The idea is to provide the detailed description of function maga, upgrading it to status of special functions.
It may have sense to consider first the function naga defined as
naga\((p )=\displaystyle \int_0^\infty \mathrm{kori}(x)^2\, \exp(\mathrm i p x) \, \mathrm d x\)
then \(~\) maga\((z)=1-\mathrm{naga}(z)\, \mathrm{naga}(z^*)^*\)
Several articles about the functions introduced above are expected to be loaded. Then it will be possible to choose the most efficient way of representation and description of function maga, using some of these functions. Some of them ar already loaded, in particular, mori and naga.
The names of the functions are tentative; they may become subject to reconsider for the analysis of the expansion of the mode of the pinhole waveguide with respect to the Bessel modes (and more accurate estimate of the loss in such a waveguide).
References
Keywords
Bessel function, kori, Korifit76, Morinaga function, mori, nori, pinhole waveguide pinhole waveguide