Difference between revisions of "SuperFactorial"
(Removed redirect to SuperFactorial) (Tag: Removed redirect) |
|||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{top}} |
||
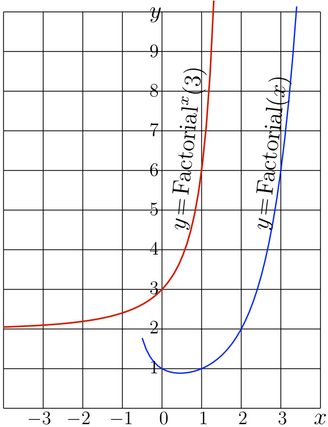
| − | [[File:Superfactorea500.png|right|300px|thumb|Fig.1. $y\!=\!x!$ and $y\!=\! \mathrm{SuperFactorial}(x)$ versus real $x$]] |
||
| + | <div style="float:right; margin:-64px 0px 8px 12px"> |
||
| + | {{pic|Superfactorea500.png|328px}} |
||
| + | <small><center>Fig.1. \(y\!=\!x!\) and \(y\!=\! \mathrm{SuperFactorial}(x)\) versus real \(x\)</center></small> |
||
| + | </div> |
||
'''SuperFactorial''', or "superfactorial" is [[superfunction]] of [[factorial]] constructed at its [[fixed point]] 2. |
'''SuperFactorial''', or "superfactorial" is [[superfunction]] of [[factorial]] constructed at its [[fixed point]] 2. |
||
| − | The smallest integer larger than 2 (id est 3) is chosen as its value at zero, |
+ | The smallest integer larger than 2 (id est 3) is chosen as its value at zero, \(\mathrm{SuperFactorial}(0)=3~\). Then,<br> |
| − | + | \(\mathrm{SuperFactorial}(1)\) \(=\) \(3!\) \(=\) \(6\), <br> |
|
| − | + | \(\mathrm{SuperFactorial}(2)=6!=720\), <br> |
|
| − | + | \(\mathrm{SuperFactorial}(3)=720!~\) and so on;<br> |
|
| − | : |
+ | : \(\mathrm{SuperFactorial}(z)=\mathrm{Factorial}^z(3)\) |
Here, the upper index of a function indicates the number of [[iteration]]s. |
Here, the upper index of a function indicates the number of [[iteration]]s. |
||
Superfactorial satisfies the [[transfer equation]] |
Superfactorial satisfies the [[transfer equation]] |
||
| − | : |
+ | : \(\mathrm{Factorial}(\mathrm{SuperFactorial}(z))=\mathrm{SuperFactorial}(z\!+\!1)\) |
SuperFactorial |
SuperFactorial |
||
| Line 20: | Line 24: | ||
http://mathworld.wolfram.com/Hyperfactorial.html |
http://mathworld.wolfram.com/Hyperfactorial.html |
||
</ref>, expressed with |
</ref>, expressed with |
||
| − | : |
+ | : \(\displaystyle \mathrm{Hyperfactorial}(n)=\prod_{k=1}^{n}k^k\) |
for integer values of the argument and with relatively simple integral |
for integer values of the argument and with relatively simple integral |
||
for the complex values. |
for the complex values. |
||
==Nest== |
==Nest== |
||
Superfactorial can be expressed through the [[Mathematica]] built-in function [[Nest]], |
Superfactorial can be expressed through the [[Mathematica]] built-in function [[Nest]], |
||
| − | : |
+ | : \(\mathrm{SuperFactorial}[z]=\mathrm{Nest}[\mathrm{Factorial}, 3, z]\) |
| − | For |
+ | For \(z\in \mathbb N\), such an expression is recognized correctly. |
<ref name="mathnest"> |
<ref name="mathnest"> |
||
However, in the current (for year 2011) implementation of [[Nest]] function in the Mathematica software allows to evaluate the SuperFactorial only for very few values of the argument; in the most of cases, the attempt to use the Nest function for evaluation of SuperFactorial causes the only diagnostic message and cannot be used to plot the SuperFactorial.</ref> |
However, in the current (for year 2011) implementation of [[Nest]] function in the Mathematica software allows to evaluate the SuperFactorial only for very few values of the argument; in the most of cases, the attempt to use the Nest function for evaluation of SuperFactorial causes the only diagnostic message and cannot be used to plot the SuperFactorial.</ref> |
||
| − | + | \(\mathrm{SuperFactorial}(z)\) is just \(z\)th iteration of Fatorial, evaluated at 3; so, |
|
| − | : |
+ | : \(\mathrm{SuperFactorial}(0)=3\) |
| − | : |
+ | : \(\mathrm{SuperFactorial}(1)=\mathrm{Factorial}(\mathrm{SuperFactorial}(0))=\mathrm{Factorial}(3)=6\) |
| − | : |
+ | : \(\mathrm{SuperFactorial}(2)=\mathrm{Factorial}^2(3)=\mathrm{Factorial} |
| − | \big( \mathrm{Factorial}(3)\big)=\mathrm{Factorial}(6)=6!=720 |
+ | \big( \mathrm{Factorial}(3)\big)=\mathrm{Factorial}(6)=6!=720\) |
| − | : |
+ | : \(\mathrm{SuperFactorial}(3)=\mathrm{Factorial}^3(3)=\mathrm{Factorial}(720)=720!\) |
| − | : |
+ | : \(\mathrm{SuperFactorial}(4)=\mathrm{Factorial}^4(3)=\mathrm{Factorial}(720!) ~\) |
and so on; however, the factorial of 720 is already too big and cannot be shown here as integer constant. Along the real axis, the SuperFactorial grows up faster than [[tetration]] does. |
and so on; however, the factorial of 720 is already too big and cannot be shown here as integer constant. Along the real axis, the SuperFactorial grows up faster than [[tetration]] does. |
||
| + | |||
| + | Up to year 2024, the Mathematica function [[Nest]] is implemented only for positive integer values of the number of the last argument. Attempts to use it in other ways causes the error messages. |
||
==History== |
==History== |
||
| Line 45: | Line 51: | ||
D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12. |
D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12. |
||
</ref>. |
</ref>. |
||
| − | That publication defined the |
+ | That publication defined the \(\sqrt{!\,}\) as holomorphic function, |
giving sense to the logo of the Physics Department of that University. |
giving sense to the logo of the Physics Department of that University. |
||
| − | As a |
+ | As a by-product, the [[SuperFunction]] of Factorial and that for some other special functions are considered there. |
Below, one of superfunctions of factorial is called SuperFactorial. |
Below, one of superfunctions of factorial is called SuperFactorial. |
||
<!-- |
<!-- |
||
| − | Aiming the evaluation of |
+ | Aiming the evaluation of \(\sqrt{!\,}\), |
value SuperFactorial(0) is not adjusted there, it is used as it comes from the [[regular iteration]] while the coefficient with the leading exponential is just unity. |
value SuperFactorial(0) is not adjusted there, it is used as it comes from the [[regular iteration]] while the coefficient with the leading exponential is just unity. |
||
| − | Then the SuperFactorial appears as iteration of factorial, evaluated at about |
+ | Then the SuperFactorial appears as iteration of factorial, evaluated at about \(3.8\); however, the integer value at zero is simpler to deal with. |
!--> |
!--> |
||
The more detailed historic overview is presented in the article [[Square root of factorial]]. |
The more detailed historic overview is presented in the article [[Square root of factorial]]. |
||
==Regular iteration== |
==Regular iteration== |
||
| − | The straightforward application of the [[regular iteration]] to the solution |
+ | The straightforward application of the [[regular iteration]] to the solution \(F\) of the [[transfer equation]] |
| − | : |
+ | :\( (1)~ ~ ~ ~ ~ F(z\!+\!1) = \mathrm{Factorial}(F(z))\) |
is described below. |
is described below. |
||
| − | Aiming to build–up the growing function, the biggest among the real [[fixed point]]s of factorial should be chosen as value at |
+ | Aiming to build–up the growing function, the biggest among the real [[fixed point]]s of factorial should be chosen as value at \(-\infty\), so, search the solution in the following form: |
| − | : |
+ | :\((2)~ ~ ~ ~ ~ F(z)=2+ a_1 \varepsilon + a_2 \varepsilon^2 +..\) |
where |
where |
||
| − | : |
+ | :\((3)~ ~ ~ ~ ~ \varepsilon=\exp(kz)\) |
| − | It is convenient to set |
+ | It is convenient to set \(a_1=1~\). Then other coefficients \(a\) and constant \(k\) can be determined substituting such a representation into the transfer equation (1): |
| − | : |
+ | :\((4) ~ ~ ~ ~ ~ \mathrm{Factoral}(2+ \varepsilon + a_2 \varepsilon^2 +..) - (2+ K \varepsilon + K^2 a_2 \varepsilon^2 +..)=0\) |
| − | where |
+ | where \(K=\exp(k)\). The expansion of the left hand side of equation (1) into the power series with respect to \(\varepsilon\) and equalizing to zero the coefficients gives the equation for \(K\) and those for \(a_2\), \(a_3\), .. For example, |
| − | : |
+ | : \(\mathrm{Factorial}'(2)-K=0\) |
| − | : |
+ | : \(\mathrm{Factorial}'(2) a_2+\mathrm{Factorial}''(2)\frac{1}{2} a_1^2-K^2 a_2=0\) |
The derivatives of Factorial are known, in particular, |
The derivatives of Factorial are known, in particular, |
||
| − | : |
+ | : \(\mathrm{Factorial}'(2)=3-2 \gamma\), |
| − | : |
+ | : \(\mathrm{Factorial}''(2)= 2 - 6 \gamma + 2 \gamma^2 + \pi^2/3\) |
| − | where |
+ | where \(\gamma=-\mathrm{Factorial}'(0) \approx -0.5772156649015329\) is the [[Euler constant]]. |
Then, |
Then, |
||
| − | : |
+ | : \(K=3-2\gamma~\) ; \(~ ~ ~k=\ln(K)=\ln(3-2\!~\gamma) \approx 0.6127874523307\) <!--0836381366079008240243 !--> |
| − | : |
+ | : \(a_2=\frac{\pi^2+6\gamma^{2}-18\gamma+6}{12(3-5\gamma+2\gamma^{2})} \approx 0.79873183517243454\) <!--1585621072345730147!--> |
| − | and similar expressions for higher coefficients |
+ | and similar expressions for higher coefficients \(a\). |
| − | The series (2) diverges, but the equation (1) allow to transfer the approximation from the range where it is valid (sufficient values of |
+ | The series (2) diverges, but the equation (1) allow to transfer the approximation from the range where it is valid (sufficient values of \(-\Re(z)\) to other values and therefore get the required precision of evaluation of \(F\). <!--with the asymptotic series.!--> |
In order to satisfy condition SuperFactorial(0)=3, it is sufficient to set |
In order to satisfy condition SuperFactorial(0)=3, it is sufficient to set |
||
| − | : |
+ | : \(\mathrm{SuperFactorial}(z)=F(x_0\!+\!z)\) |
| − | where |
+ | where \(~x_0\!\approx\! -0.91938596545217788~\) is solution of equation \(~F(x_0)\!=\!3~\). |
==Properties of Superfactorial== |
==Properties of Superfactorial== |
||
| + | <div style="float:right; margin:-24px 0px 16px 8px;"> |
||
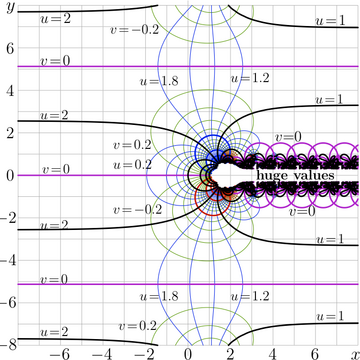
| − | [[File:Superfactocomple1.png|right|400px| thumb|Fig.2. [[Complex map]] of $f=\mathrm{SuperFactorial}(x+\mathrm i y)$ in the $x,y$ plane; levels |
||
| + | {{pic|Superfactocomple1.png|360px}}<small><center>Fig.2. \(u+\mathrm i v=\mathrm{SuperFactorial}(x\!+\!\mathrm i y)\). |
||
| − | $u=\Re(f)=$const and |
||
| + | </small></center></div> |
||
| − | $v=\Im(f)=$const are drawn]] |
||
| − | The [[complex map]] of SuperFactorial is shown at the figure 2. |
+ | The [[complex map]] of SuperFactorial is shown at the figure 2. The [[contour plot]]s of<br> |
| + | \( u\!=\!\Re(\mathrm {SuperFactorial} (x\!+\!\mathrm i y)\) and<br> |
||
| − | <!-- |
||
| + | \( v\!=\!\Im(\mathrm {SuperFactorial} (x\!+\!\mathrm i y)\)<br> |
||
| − | at right. The [[contour plot]]s of<br> |
||
| − | $ u\!=\!\Re(\mathrm {SuperFactorial} (x\!+\!\mathrm i y)$ and<br> |
||
| − | $ v\!=\!\Im(\mathrm {SuperFactorial} (x\!+\!\mathrm i y)$<br> |
||
intersect on the right angles, as they are supposed to do at the complex map of any [[holomorphic function]]. |
intersect on the right angles, as they are supposed to do at the complex map of any [[holomorphic function]]. |
||
| − | The integer values of |
+ | The integer values of \(u\) or \(v\) are marked with thick lines; thin lines correspond to the intermediate levels. |
| − | !--> |
||
| − | SuperFactorial is [[real-holomorphic]], at lest in the range |
+ | SuperFactorial is [[real-holomorphic]], at lest in the range \(\{z \in \mathbb C : \Re(z)\le 2\}\). |
<!-- |
<!-- |
||
| − | + | \(\mathrm{SuperFactorial}(z^*)= \mathrm{SuperFactorial}(z)^*\) |
|
| − | for all |
+ | for all \(z\( from the range of the definition. |
!--> |
!--> |
||
SuperFactorial is [[periodic function]]; the period |
SuperFactorial is [[periodic function]]; the period |
||
| + | |||
| − | : $T=\frac{2 \pi \mathrm i}{k} \approx 10.2534496811560279265772640691397~\mathrm i$ |
||
| + | \(P = \frac{2 \pi \mathrm i}{k} \approx 10.2534496811560279265772640691397~\mathrm i\) |
||
At non-negative integer values of the argument, SuperFactorial takes integer values; in particular, |
At non-negative integer values of the argument, SuperFactorial takes integer values; in particular, |
||
| − | + | \(\mathrm{SuperFactorial}(0)=3~\) |
|
| − | Function |
+ | Function \(\tilde F(z)=\mathrm{SuperFactorial}\left(z+\frac{T}{2}\right)\) is also [[real-holomorphic]]; it smoothly decreases from value 2 at \(-\infty\) to unity at \(+\infty\) along the real axis. Such a complementary superfunction typically exists at the consruction of a superfunction with [[regular iteration]] at a real [[fixed point]]. |
==Singularities== |
==Singularities== |
||
| + | <div class="thumb tright" style="float:right; margin:0px 0px 4px 16px; width:360px"> |
||
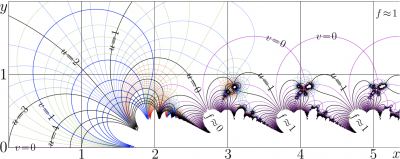
| − | [[File:Sfaczoo300.png|right|500px|thumb|Fig.3. Zoom-in from Fig.2. |
||
| + | {{pic|Sfaczoo300.png|400px}}<small><center> Fig.3. Zoom-in from Fig.2.<!-- |
||
| − | <!--complex map of SuperFactorial, $f\!=\!\mathrm{SuperFactorial}(x\!+\!\mathrm i y)$; levels |
||
| + | \( u+\mathrm i v = \mathrm{SuperFactorial}(x\!+\!\mathrm i y)\);--> |
||
| − | $u\!=\!\Re(f)=$const and |
||
| + | </center></small> |
||
| − | $v\!=\!\Im(f)=$const are drawn!-->]] |
||
| + | </div> |
||
| − | FuperFactorial is not [[entire function]], over-vice, it would have negative integer values somewhere, which is not consistent with the transfer equation (1): Factorial at negative integers has poles. The unity translation form any point, where the SuperFactorial has negative integer value leads to a singularity. |
||
| + | SuperFactorial is not [[entire function]], over-vice, it would have negative integer values somewhere, which is not consistent with the transfer equation (1): Factorial at negative integers has poles. The unity translation form any point, where the SuperFactorial has negative integer value leads to a singularity. |
||
The conclusion about the singularities is confirmed by the zoom-in from the comlpex map of the SuperFactorial. The figure indicates that the singularities of SuperFactorial are located within half-strips |
The conclusion about the singularities is confirmed by the zoom-in from the comlpex map of the SuperFactorial. The figure indicates that the singularities of SuperFactorial are located within half-strips |
||
| − | : |
+ | : \( z\in \mathbb C :\) \( \{ \Re(z) >\!2.7 ~,~ |\Im(z)\!+\!T n|<1 ~\mathrm{for~ some~} n\in \mathbb Z \}\) |
| − | Outside these half-strips, the SuperFactorial exponentially approaches 2 as the real part of the argument goes to |
+ | Outside these half-strips, the SuperFactorial exponentially approaches 2 as the real part of the argument goes to \(-\!\infty\) and approaches unity as |
| − | the real part of the argument goes to |
+ | the real part of the argument goes to \(+\!\infty\). |
==AbelFactorial== |
==AbelFactorial== |
||
The inverse function of SuperFactorial is [[AbelFactorial]]; at least in some vicinity of the [[half-line]] along the real axis, the relations |
The inverse function of SuperFactorial is [[AbelFactorial]]; at least in some vicinity of the [[half-line]] along the real axis, the relations |
||
| − | : |
+ | : \(\mathrm{SuperFactorial}( |
| − | \mathrm{AbelFactorial}(z))=z |
+ | \mathrm{AbelFactorial}(z))=z\) |
| − | : |
+ | : \(\mathrm{AbelFactorial}( |
| − | \mathrm{SuperFactorial}(z))=z |
+ | \mathrm{SuperFactorial}(z))=z\) |
The AbelFactorial satisfies the [[Abel equation]] |
The AbelFactorial satisfies the [[Abel equation]] |
||
| − | : |
+ | : \(\mathrm{Abelfactorial}( \mathrm{Factorial}(z))= \mathrm{AbelFactorial}(z)+1\) |
See the special article [[AbelFactorial]] for the details. |
See the special article [[AbelFactorial]] for the details. |
||
| − | Together, the |
+ | Together, the AbelFactorial and the SuperFactorial allow to express (and to evaluate) the iterations of Factorial in the following way: |
| − | : |
+ | : \(\mathrm{Factorial}^c(z)=\mathrm{SuperFactorial}\big(c + \mathrm{AbelFactorial}(z)\big)\) |
| − | where number |
+ | where number \(c\) of iterations has no need to be integer; it can be even complex, and for some domain of \(c,d,z\in C^3 \subseteq \mathbb C^3\), the relation |
| − | : |
+ | : \(\mathrm{Factorial}^c\big(\mathrm{Factorial}^d(z)\big)=\mathrm{Factorial}^{c+d}((z)\) |
as if takes place for the exponentiation. This justifies the notation [[square root of factorial]] for the half–iteration of Factorial, id est |
as if takes place for the exponentiation. This justifies the notation [[square root of factorial]] for the half–iteration of Factorial, id est |
||
| − | : |
+ | : \(\sqrt{!~}~=~\mathrm{Factorial}^{1/2}\) |
| − | In wide domain of values of |
+ | In wide domain of values of \(z\), the relation |
| − | : |
+ | : \(\sqrt{!~}~(\sqrt{!~}(z))~=~\mathrm{Factorial}(z)=z!\) |
| − | See the special article [[ |
+ | See the special article «[[Square root of factorial]]» for the details. |
==Existence and uniqueness== |
==Existence and uniqueness== |
||
| Line 153: | Line 158: | ||
The new superfunctions of Factorial can be constructed with periodic perturbation of its argument, let |
The new superfunctions of Factorial can be constructed with periodic perturbation of its argument, let |
||
| − | : |
+ | : \(f(z)=\mathrm{SuperFactorial}(z+\zeta(z))\) |
| − | where |
+ | where \(\zeta\) is some hoomorphic function, periodic with period unity. |
| − | Function |
+ | Function \(f\) satisfies the same transfer equation {1} as the SuperFactorial; |
| − | however, the periodicity or |
+ | however, the periodicity or \(\zeta\) does not allow it to decay as the real part of the argument goes \(-\infty\); |
| − | as the result, neither the asymptotic behavior (2) of the SuperFactorial, nor its periodicity with period |
+ | as the result, neither the asymptotic behavior (2) of the SuperFactorial, nor its periodicity with period \(T\) can be achieved. |
In this sense, with specification of the asymptotic behavior and the periodicity, the SuperFactorial is unique. |
In this sense, with specification of the asymptotic behavior and the periodicity, the SuperFactorial is unique. |
||
| Line 179: | Line 184: | ||
The call of such a function may have form |
The call of such a function may have form |
||
:'''Nest[f,a,z]''' |
:'''Nest[f,a,z]''' |
||
| − | where |
+ | where \(f\) indicates the name of the function, \(z\) is number of iterations, and \(a\) is initial value. |
| − | Then, |
+ | Then, \(\mathrm{SuperFactorial}(z)\) can be expressed with |
: '''Nest[Factorial,3,z]''' |
: '''Nest[Factorial,3,z]''' |
||
| − | and the |
+ | and the \(c\)th iteration of [[Factorial]], id est, \(\mathrm{Factorial}^c(z)\) could be written as |
: '''Nest[Factorial,z,c]''' |
: '''Nest[Factorial,z,c]''' |
||
| Line 196: | Line 201: | ||
==Conclusions== |
==Conclusions== |
||
| − | From the point of view of construction of [[superfunction]]s, there is nothing specific in the Factorial: the SuperFactorial is constructed in the same way as superfunction for |
+ | From the point of view of construction of [[superfunction]]s, there is nothing specific in the Factorial: the SuperFactorial is constructed in the same way as superfunction for \(\exp_b\) for \(1<b<\exp(1/\mathrm e)\), described in <ref name="sqrt2"/> or that for the [[logistic operator]] |
<ref name="logistic"> |
<ref name="logistic"> |
||
http://www.springerlink.com/content/u712vtp4122544x4 |
http://www.springerlink.com/content/u712vtp4122544x4 |
||
| Line 202: | Line 207: | ||
</ref>. |
</ref>. |
||
| − | SupeFactorial, together with its inverse function (id est, [[AbelFactorial]]) allows to define the |
+ | SupeFactorial, together with its inverse function (id est, [[AbelFactorial]]) allows to define the \(c\)th iteration of factorial for non-integer values of \(c\); in particilar, the [[square root of factorial]] (that was believed to have no sense |
<ref name="kandidov"> |
<ref name="kandidov"> |
||
| + | https://www.phys.msu.ru/rus/about/sovphys/ISSUES-2007/5(58)-2007/58-5/ |
||
| − | http://ofvp.phys.msu.ru/pdf/Kandidov_70.pdf: |
||
| + | <!-- The previous URL http://ofvp.phys.msu.ru/pdf/Kandidov_70.pdf: |
||
| − | V.P.Kandidov. About the time and myself. (In Russian) |
||
| + | is nor valid anymore !--> |
||
| − | <blockquote>По итогам студенческого голосования победителями оказались значок с изображением |
||
| + | V.P.Kandidov. About the time and myself. 1987.05.18. (In Russian) .. |
||
| + | О ВРЕМЕНИ И ФАКУЛЬТЕТЕ, О КАФЕДРЕ И О СЕБЕ. 70-тилетие профессора В.П.Кандидова. .. « |
||
| + | По итогам студенческого голосования победителями оказались значок с изображением |
||
рычага, поднимающего Землю, и нынешний с хорошо известной эмблемой в виде |
рычага, поднимающего Землю, и нынешний с хорошо известной эмблемой в виде |
||
корня из факториала, вписанными в букву Ф. Этот значок, созданный студентом |
корня из факториала, вписанными в букву Ф. Этот значок, созданный студентом |
||
| Line 212: | Line 220: | ||
выразительностью. Тогда эмблема этого значка подверглась жесткой критике со |
выразительностью. Тогда эмблема этого значка подверглась жесткой критике со |
||
стороны руководства факультета, поскольку она не имеет физического смысла, |
стороны руководства факультета, поскольку она не имеет физического смысла, |
||
| − | математически абсурдна и идеологически бессодержательна. |
+ | математически абсурдна и идеологически бессодержательна. ..» |
| + | </ref><ref name="naukai"><!-- |
||
| − | </blockquote> |
||
| + | The previous URL is not valid anymore |
||
| − | </ref><ref name="naukai"> |
||
| − | http://nauka.relis.ru/11/0412/11412002.htm |
+ | http://nauka.relis.ru/11/0412/11412002.htm !--> |
| + | https://www.nkj.ru/archive/articles/1023/ |
||
250 anniversary of the Moscow State University. (In Russian) |
250 anniversary of the Moscow State University. (In Russian) |
||
| − | ПЕРВОМУ УНИВЕРСИТЕТУ СТРАНЫ - 250! |
+ | ПЕРВОМУ УНИВЕРСИТЕТУ СТРАНЫ - 250! |
| + | Наука и жизнь, 2005, N1 |
||
| − | <blockquote> |
||
| − | На значке физфака в букву "Ф" вписано стилизованное изображение корня из факториала (√!) - выражение, математического смысла не имеющее. |
+ | «На значке физфака в букву "Ф" вписано стилизованное изображение корня из факториала (√!) - выражение, математического смысла не имеющее.» |
| + | </ref>). appears as half-iteratiopn of factorial. This symbol of this function, id est, \(\sqrt{!\,}\) is used as central |
||
| − | </blockquote> |
||
| − | </ref>). appears as half-iteratiopn of factorial. This symbol of this function, id est, $\sqrt{!\,}$ is used as central |
||
part of logo of [[TORI]]. |
part of logo of [[TORI]]. |
||
==References== |
==References== |
||
| + | {{ref}} |
||
| − | <references/> |
||
| + | {{fer}} |
||
| + | |||
| + | ==Keywords== |
||
| + | |||
| + | «[[AbelFactorialR.png]]», |
||
| + | «[[ArcCosc]]», |
||
| + | «[[Complex map]]», |
||
| + | «[[FacIteT.jpg]]», |
||
| + | «[[Factorial]]», |
||
| + | «[[IterfacPlotT.png]]», |
||
| + | «[[Iteration]]», |
||
| + | «[[Mathematica]]», |
||
| + | «[[Moscow University Physics Bulletin]]», |
||
| + | «[[Name of function]]», |
||
| + | «[[Pentation]]», |
||
| + | «[[QFacMapT.png]]», |
||
| + | «[[QFactorialQexp.jpg]]», |
||
| + | «[[Regular Iteration]]», |
||
| + | «[[Sfaczoo300.png]]», |
||
| + | «[[Special function]]», |
||
| + | «[[SuFac]]», |
||
| + | «[[SuperFactorial.cin]]», |
||
| + | «[[Superfactorial.cin]]», |
||
| + | «[[Superfactorial]] (That caused fonfusions)», |
||
| + | «[[Superfunction]]», |
||
| + | «[[Superfunctions]]», |
||
| + | «[[Square root of factorial]]», |
||
| + | «[[Square root of exponential]]», |
||
| + | «[[SuZex]]», |
||
| + | «[[SuZex approximation]]», |
||
| + | «[[SuperFacMapT.png]]», |
||
| + | «[[SuperFacPlotT.png]]», |
||
| + | «[[Superfactocomple1.png]]», |
||
| + | «[[Superfactorea500.png]]», |
||
| + | «[[SuperFacZoomT.png]]», |
||
| + | «[[Superfac.cin]]», |
||
| + | «[[Superfunctions]]», |
||
| + | «[[Table of superfunctions]]», |
||
| + | [[Category:SuFac]] |
||
[[Category:Superfunction]] |
[[Category:Superfunction]] |
||
[[Category:SuperFactorial]] |
[[Category:SuperFactorial]] |
||
[[Category:Factorial]] |
[[Category:Factorial]] |
||
[[Category:Holomorphic function]] |
[[Category:Holomorphic function]] |
||
| − | [[Category: |
+ | [[Category:English]] |
Latest revision as of 00:03, 29 February 2024
SuperFactorial, or "superfactorial" is superfunction of factorial constructed at its fixed point 2.
The smallest integer larger than 2 (id est 3) is chosen as its value at zero, \(\mathrm{SuperFactorial}(0)=3~\). Then,
\(\mathrm{SuperFactorial}(1)\) \(=\) \(3!\) \(=\) \(6\),
\(\mathrm{SuperFactorial}(2)=6!=720\),
\(\mathrm{SuperFactorial}(3)=720!~\) and so on;
- \(\mathrm{SuperFactorial}(z)=\mathrm{Factorial}^z(3)\)
Here, the upper index of a function indicates the number of iterations.
Superfactorial satisfies the transfer equation
- \(\mathrm{Factorial}(\mathrm{SuperFactorial}(z))=\mathrm{SuperFactorial}(z\!+\!1)\)
SuperFactorial [1] should not be confused with hyperfactorial [2], expressed with
- \(\displaystyle \mathrm{Hyperfactorial}(n)=\prod_{k=1}^{n}k^k\)
for integer values of the argument and with relatively simple integral for the complex values.
Contents
Nest
Superfactorial can be expressed through the Mathematica built-in function Nest,
- \(\mathrm{SuperFactorial}[z]=\mathrm{Nest}[\mathrm{Factorial}, 3, z]\)
For \(z\in \mathbb N\), such an expression is recognized correctly. [3]
\(\mathrm{SuperFactorial}(z)\) is just \(z\)th iteration of Fatorial, evaluated at 3; so,
- \(\mathrm{SuperFactorial}(0)=3\)
- \(\mathrm{SuperFactorial}(1)=\mathrm{Factorial}(\mathrm{SuperFactorial}(0))=\mathrm{Factorial}(3)=6\)
- \(\mathrm{SuperFactorial}(2)=\mathrm{Factorial}^2(3)=\mathrm{Factorial} \big( \mathrm{Factorial}(3)\big)=\mathrm{Factorial}(6)=6!=720\)
- \(\mathrm{SuperFactorial}(3)=\mathrm{Factorial}^3(3)=\mathrm{Factorial}(720)=720!\)
- \(\mathrm{SuperFactorial}(4)=\mathrm{Factorial}^4(3)=\mathrm{Factorial}(720!) ~\)
and so on; however, the factorial of 720 is already too big and cannot be shown here as integer constant. Along the real axis, the SuperFactorial grows up faster than tetration does.
Up to year 2024, the Mathematica function Nest is implemented only for positive integer values of the number of the last argument. Attempts to use it in other ways causes the error messages.
History
First, the superfunction of factorial is described in 2010 in the Moscow University Physics Bulletin [1]. That publication defined the \(\sqrt{!\,}\) as holomorphic function, giving sense to the logo of the Physics Department of that University. As a by-product, the SuperFunction of Factorial and that for some other special functions are considered there. Below, one of superfunctions of factorial is called SuperFactorial. The more detailed historic overview is presented in the article Square root of factorial.
Regular iteration
The straightforward application of the regular iteration to the solution \(F\) of the transfer equation
- \( (1)~ ~ ~ ~ ~ F(z\!+\!1) = \mathrm{Factorial}(F(z))\)
is described below.
Aiming to build–up the growing function, the biggest among the real fixed points of factorial should be chosen as value at \(-\infty\), so, search the solution in the following form:
- \((2)~ ~ ~ ~ ~ F(z)=2+ a_1 \varepsilon + a_2 \varepsilon^2 +..\)
where
- \((3)~ ~ ~ ~ ~ \varepsilon=\exp(kz)\)
It is convenient to set \(a_1=1~\). Then other coefficients \(a\) and constant \(k\) can be determined substituting such a representation into the transfer equation (1):
- \((4) ~ ~ ~ ~ ~ \mathrm{Factoral}(2+ \varepsilon + a_2 \varepsilon^2 +..) - (2+ K \varepsilon + K^2 a_2 \varepsilon^2 +..)=0\)
where \(K=\exp(k)\). The expansion of the left hand side of equation (1) into the power series with respect to \(\varepsilon\) and equalizing to zero the coefficients gives the equation for \(K\) and those for \(a_2\), \(a_3\), .. For example,
- \(\mathrm{Factorial}'(2)-K=0\)
- \(\mathrm{Factorial}'(2) a_2+\mathrm{Factorial}''(2)\frac{1}{2} a_1^2-K^2 a_2=0\)
The derivatives of Factorial are known, in particular,
- \(\mathrm{Factorial}'(2)=3-2 \gamma\),
- \(\mathrm{Factorial}''(2)= 2 - 6 \gamma + 2 \gamma^2 + \pi^2/3\)
where \(\gamma=-\mathrm{Factorial}'(0) \approx -0.5772156649015329\) is the Euler constant. Then,
- \(K=3-2\gamma~\) ; \(~ ~ ~k=\ln(K)=\ln(3-2\!~\gamma) \approx 0.6127874523307\)
- \(a_2=\frac{\pi^2+6\gamma^{2}-18\gamma+6}{12(3-5\gamma+2\gamma^{2})} \approx 0.79873183517243454\)
and similar expressions for higher coefficients \(a\).
The series (2) diverges, but the equation (1) allow to transfer the approximation from the range where it is valid (sufficient values of \(-\Re(z)\) to other values and therefore get the required precision of evaluation of \(F\).
In order to satisfy condition SuperFactorial(0)=3, it is sufficient to set
- \(\mathrm{SuperFactorial}(z)=F(x_0\!+\!z)\)
where \(~x_0\!\approx\! -0.91938596545217788~\) is solution of equation \(~F(x_0)\!=\!3~\).
Properties of Superfactorial
The complex map of SuperFactorial is shown at the figure 2. The contour plots of
\( u\!=\!\Re(\mathrm {SuperFactorial} (x\!+\!\mathrm i y)\) and
\( v\!=\!\Im(\mathrm {SuperFactorial} (x\!+\!\mathrm i y)\)
intersect on the right angles, as they are supposed to do at the complex map of any holomorphic function.
The integer values of \(u\) or \(v\) are marked with thick lines; thin lines correspond to the intermediate levels.
SuperFactorial is real-holomorphic, at lest in the range \(\{z \in \mathbb C : \Re(z)\le 2\}\).
SuperFactorial is periodic function; the period
\(P = \frac{2 \pi \mathrm i}{k} \approx 10.2534496811560279265772640691397~\mathrm i\)
At non-negative integer values of the argument, SuperFactorial takes integer values; in particular, \(\mathrm{SuperFactorial}(0)=3~\)
Function \(\tilde F(z)=\mathrm{SuperFactorial}\left(z+\frac{T}{2}\right)\) is also real-holomorphic; it smoothly decreases from value 2 at \(-\infty\) to unity at \(+\infty\) along the real axis. Such a complementary superfunction typically exists at the consruction of a superfunction with regular iteration at a real fixed point.
Singularities
SuperFactorial is not entire function, over-vice, it would have negative integer values somewhere, which is not consistent with the transfer equation (1): Factorial at negative integers has poles. The unity translation form any point, where the SuperFactorial has negative integer value leads to a singularity.
The conclusion about the singularities is confirmed by the zoom-in from the comlpex map of the SuperFactorial. The figure indicates that the singularities of SuperFactorial are located within half-strips
- \( z\in \mathbb C :\) \( \{ \Re(z) >\!2.7 ~,~ |\Im(z)\!+\!T n|<1 ~\mathrm{for~ some~} n\in \mathbb Z \}\)
Outside these half-strips, the SuperFactorial exponentially approaches 2 as the real part of the argument goes to \(-\!\infty\) and approaches unity as the real part of the argument goes to \(+\!\infty\).
AbelFactorial
The inverse function of SuperFactorial is AbelFactorial; at least in some vicinity of the half-line along the real axis, the relations
- \(\mathrm{SuperFactorial}( \mathrm{AbelFactorial}(z))=z\)
- \(\mathrm{AbelFactorial}( \mathrm{SuperFactorial}(z))=z\)
The AbelFactorial satisfies the Abel equation
- \(\mathrm{Abelfactorial}( \mathrm{Factorial}(z))= \mathrm{AbelFactorial}(z)+1\)
See the special article AbelFactorial for the details.
Together, the AbelFactorial and the SuperFactorial allow to express (and to evaluate) the iterations of Factorial in the following way:
- \(\mathrm{Factorial}^c(z)=\mathrm{SuperFactorial}\big(c + \mathrm{AbelFactorial}(z)\big)\)
where number \(c\) of iterations has no need to be integer; it can be even complex, and for some domain of \(c,d,z\in C^3 \subseteq \mathbb C^3\), the relation
- \(\mathrm{Factorial}^c\big(\mathrm{Factorial}^d(z)\big)=\mathrm{Factorial}^{c+d}((z)\)
as if takes place for the exponentiation. This justifies the notation square root of factorial for the half–iteration of Factorial, id est
- \(\sqrt{!~}~=~\mathrm{Factorial}^{1/2}\)
In wide domain of values of \(z\), the relation
- \(\sqrt{!~}~(\sqrt{!~}(z))~=~\mathrm{Factorial}(z)=z!\)
See the special article «Square root of factorial» for the details.
Existence and uniqueness
The existence and uniquness of a SuperFunction for a holomorphic fixed point is considered in [4]. The regular iteration gives the explicit proof of existence, while the requirements on the behavior at zero and the asymptotic properties provide the uniqueness. However, there are many other fixed points, and each of them can be used to construct a superfunction of factorial, pretty different from the SuperFactorial described above.
The new superfunctions of Factorial can be constructed with periodic perturbation of its argument, let
- \(f(z)=\mathrm{SuperFactorial}(z+\zeta(z))\)
where \(\zeta\) is some hoomorphic function, periodic with period unity. Function \(f\) satisfies the same transfer equation {1} as the SuperFactorial; however, the periodicity or \(\zeta\) does not allow it to decay as the real part of the argument goes \(-\infty\); as the result, neither the asymptotic behavior (2) of the SuperFactorial, nor its periodicity with period \(T\) can be achieved. In this sense, with specification of the asymptotic behavior and the periodicity, the SuperFactorial is unique.
The SuperFactorial above seems to be the simplest among various SuperFunctions of Factorial, if one exclude functions that are identically equal to a constant. Other non-trivial superfunctions of Factorial show complicated behavior: and even the holomorphism in the left hand side of the complex plane cannot be achieved. Up to year 2011, a statement has status of conjecture, and the rigorous proof may be matter for the good outstanding research.
Algorithmic implementation of Superfactorial
C++ implementation
For the efficient evaluation of SuperFactorial, the regular iteration is suitable; the reasonable number of terms in the partial sum is of order of dozen. Then, within few tens of operations, one can get of order of 15 decimal digits, that is sufficient for the complex double implementation. The C++ code for the evaluation of SuperFactorial used to generate the figures is expected to be loaded, as a common component of the generators of the figures.
In the final version, the SuperFactorial is expected to be implemented as
- complex<double> SuperFactorial(complex<double> z)
and its inverse function is expected to be implemented as
- complex<double> AbelFactorial(complex<double> z)
The preliminary versions of the routines can be uploaded upon request; the final version will appear after to check the compatibility with other codes that are already loaded in TORI and in the Citizendium.
Mathematica implementation
In version of 2011, Mathematica already has name reserved for the iteration of functions, namely, Nest. The call of such a function may have form
- Nest[f,a,z]
where \(f\) indicates the name of the function, \(z\) is number of iterations, and \(a\) is initial value.
Then, \(\mathrm{SuperFactorial}(z)\) can be expressed with
- Nest[Factorial,3,z]
and the \(c\)th iteration of Factorial, id est, \(\mathrm{Factorial}^c(z)\) could be written as
- Nest[Factorial,z,c]
In the current version of Mathematica (year 2011), the Nest is implemented only for the case, when the last argument can be simplified to an constant , expressed with a natural number. [5]
The upgrade of the implementation of Nest may include the table of SuperFunctions and corresponding Abel functions, their properties and ways of the efficient evaluation with required precision.
Conclusions
From the point of view of construction of superfunctions, there is nothing specific in the Factorial: the SuperFactorial is constructed in the same way as superfunction for \(\exp_b\) for \(1<b<\exp(1/\mathrm e)\), described in [4] or that for the logistic operator [6].
SupeFactorial, together with its inverse function (id est, AbelFactorial) allows to define the \(c\)th iteration of factorial for non-integer values of \(c\); in particilar, the square root of factorial (that was believed to have no sense [7][8]). appears as half-iteratiopn of factorial. This symbol of this function, id est, \(\sqrt{!\,}\) is used as central part of logo of TORI.
References
- ↑ 1.0 1.1 http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12.
- ↑ http://mathworld.wolfram.com/Hyperfactorial.html
- ↑ However, in the current (for year 2011) implementation of Nest function in the Mathematica software allows to evaluate the SuperFactorial only for very few values of the argument; in the most of cases, the attempt to use the Nest function for evaluation of SuperFactorial causes the only diagnostic message and cannot be used to plot the SuperFactorial.
- ↑ 4.0 4.1 http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
- ↑ http://reference.wolfram.com/mathematica/ref/Nest.html BUILT-IN MATHEMATICA SYMBOL Tutorials. Nest.
- ↑ http://www.springerlink.com/content/u712vtp4122544x4 D.Kouznetsov. Holomorphic extension of the logistic sequence. Moscow University Physics Bulletin, 2010, No.2, p.91-98.
- ↑ https://www.phys.msu.ru/rus/about/sovphys/ISSUES-2007/5(58)-2007/58-5/ V.P.Kandidov. About the time and myself. 1987.05.18. (In Russian) .. О ВРЕМЕНИ И ФАКУЛЬТЕТЕ, О КАФЕДРЕ И О СЕБЕ. 70-тилетие профессора В.П.Кандидова. .. « По итогам студенческого голосования победителями оказались значок с изображением рычага, поднимающего Землю, и нынешний с хорошо известной эмблемой в виде корня из факториала, вписанными в букву Ф. Этот значок, созданный студентом кафедры биофизики А.Сарвазяном, привлекал своей простотой и выразительностью. Тогда эмблема этого значка подверглась жесткой критике со стороны руководства факультета, поскольку она не имеет физического смысла, математически абсурдна и идеологически бессодержательна. ..»
- ↑ https://www.nkj.ru/archive/articles/1023/ 250 anniversary of the Moscow State University. (In Russian) ПЕРВОМУ УНИВЕРСИТЕТУ СТРАНЫ - 250! Наука и жизнь, 2005, N1 «На значке физфака в букву "Ф" вписано стилизованное изображение корня из факториала (√!) - выражение, математического смысла не имеющее.»
Keywords
«AbelFactorialR.png», «ArcCosc», «Complex map», «FacIteT.jpg», «Factorial», «IterfacPlotT.png», «Iteration», «Mathematica», «Moscow University Physics Bulletin», «Name of function», «Pentation», «QFacMapT.png», «QFactorialQexp.jpg», «Regular Iteration», «Sfaczoo300.png», «Special function», «SuFac», «SuperFactorial.cin», «Superfactorial.cin», «Superfactorial (That caused fonfusions)», «Superfunction», «Superfunctions», «Square root of factorial», «Square root of exponential», «SuZex», «SuZex approximation», «SuperFacMapT.png», «SuperFacPlotT.png», «Superfactocomple1.png», «Superfactorea500.png», «SuperFacZoomT.png», «Superfac.cin», «Superfunctions», «Table of superfunctions»,