ArcShoka

\(u\!+\!\mathrm i v= \mathrm{ArcShoka}(x\!+\!\mathrm i y)\)

ArcShoka function is inverse function of Shoka function and Abel function for the Keller function;

\( \displaystyle \mathrm{ArcShoka}(z)= z + \ln\!\left( \frac{\mathrm e^z-1}{\mathrm e-1} \right)\)

Warning! Yet, this article is very draft

Various inverse functions

Various ways of inversion of the Shoka function lead to the same behavior along the real axis, in the same way as the Shoka function and the Shoko function have identical behavior in vicinity of the real axis; but but different directions of the cutlines.

For efficient comparison of various superfunctions \(F\) of the transfer functions \(T\) of realistic physical systems, the extension to the complex plane seems to be important tool. This allows to specify the unique solution of the Transfer equation

\( T(F(z))=F(z\!+\!1)\)

without to refer to the specific way of evaluation of superfunction (although it seems, in many cases of the laser science, the physically-meaningful superfunction can be constructed with the regular iteration). For this reason, the special article about function ArcShoka is loaded. One of goals of this article is comparison of various representations for the ArcShoka function and postulating it as the definition.

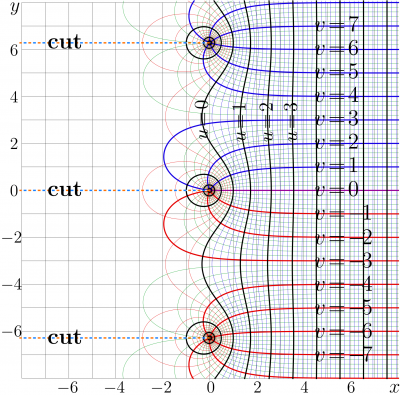
The ArcShoka shown in the complex map at right seems to be the most convenient for comparison with the Abel function of similar transfer functions for simple models of the optical media.

Behavior along the real axis

For real values of the argument, there is no need to make difference between Shoka function and Shoko function, and no need to make any difference between their inverse functions (providing that the cutline do not cross the real axis.) The explicit plot at the picture could be obtained also by the reflection of the plot for the Shoka function from the angle bisector of the First quadrant (id est, line \(y=x\)). However, for the testing and debugging of the algorithms for the construction of superfunctions and the Abel function, it is important to have the detailed descriptions for the case, when these functions can be expressed through the elementary functions.

ArcShoka as Abel function

The ArcShoka function is Abel function for the transfer function \(T=\mathrm{Keller}\); the Keller function can be defined with

\(\mathrm{Keller}(z)=\ln\!\Big(1+\mathrm e(\mathrm e^z\!−\!1)\Big)\)

at least in vicinity of the real axis. Then , the \(G=\mathrm{ArcShoka}\) satisfies the Abel equation

\(G(T(z))=G(z)+1\)

Keywords

Shoka function, Abel function, Inverserse function, Keller function