Shoko function

Shoko function and two its asimptitics

Shoko function describes the growth of the fluence of pulse of light in the homogeneous amplifier within the simple kinetics of laser medium.

The Shoko function is superfunction of the Keller function. For the analysis of the Keller function, another superfunction, namely, Shoka function happens to be more convenient. In vicinity of the real axis (and, in particular, for real values of the argument), functions Shoka and Shoko coincide.

Definiton

The Shoko function can be expressed through the elementary functions:

\( \!\!\!\!\!\!\!\!\!\! (1) ~ ~ ~ \mathrm {Shoko}(z)=\ln\Big(1+\mathrm e^z (\mathrm e -1) \Big)\)

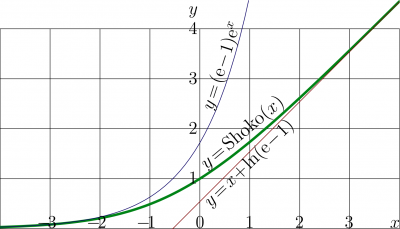
The explicit plot of Shoko function is showm in figure at right. In the same figure, the two its asimptotics are plotted,

Periodicity and cuts

\(u\!+\!\mathrm i v=\mathrm{Shoko}(x\!+\!\mathrm i y)\)

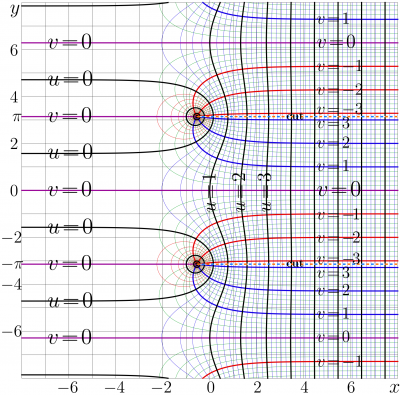
The complex map of the Shoko function is shown in figure at right.

The Shoko function is periodic; the period \(P=2 \pi \mathrm i\) is pure imaginary.

The Shoko function has series of branchpoints at \(r+\pi(1\!+\!2 n) \mathrm i\) for integer values of \(n\);

\( \displaystyle r = - \ln (\mathrm e \!-\! 1 ) \approx -0.54132485461292\)

and the series of cutlines \(r+\pi(1\!+\!2 n)\mathrm i + t\) for integer values of \(n\) and positive values of \(t\). The cutlines are along the real axis, and there is no easy way do direct them to the opposite direction, keeping the representation simple.

Asymptotic behavior

At large negative values of the real part of the argument, the Shoko function shows almost exponential growth:

\( \!\!\!\!\!\!\!\!\!\! (2) ~ ~ ~ \mathrm {Shoko}(z)= (\mathrm e -1) \mathrm e^z+ O(\mathrm e^{2z})\)

At small values of the argument, the Shoko function expands to the Taylor series as follows:

\( \!\!\!\!\!\!\!\!\!\! (3) \displaystyle ~ ~ ~\mathrm {Shoko}(z)= 1+ \frac{1}{\mathrm e} z + \frac{-1/2}{(\mathrm e\!-\!1)\mathrm e} z^2 + ..\)

Many Taylor coefficients of the expansion can be calculated with some Mathematica or Maple software; the series converges at

\( \displaystyle ~ ~ |z|< \sqrt{\pi^2\!+\!r^2} \approx 3.18788911339636\)

At large positive values of the real part of the argument, the Shoko function grows almost linearly:

\( \!\!\!\!\!\!\!\!\!\! (4) ~ ~ ~\mathrm {Shoko}(z)= \ln(\mathrm e -1) + z+ O(\mathrm e^{-z})\)

but this representation is valid only while \(|\Im(z)| <\pi\).

The asymptotic series seem to diverge at any values of \(z\), but can be used for the precise evaluation of Shoko function at large values of modulus of the real part of the argument, while the straightforward application of definition is difficult. The cut lines could be directed to the left by the price of loss of periodicity. The corresponding modification of the Shoko function is considered in the next section.

Shoka function

\(u\!+\!\mathrm i v = \mathrm{Shoka}(x\!+\mathrm i y)\)

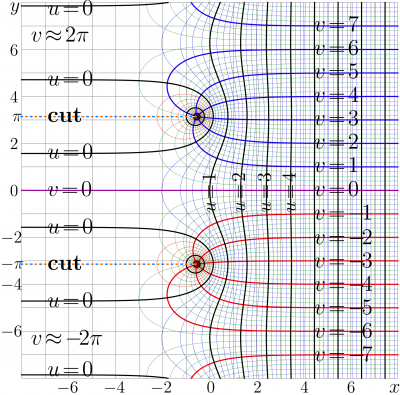
Following the tradition of TORI, it is desirable to direct the cut lines at the complex map of the function to the left. Such a modification of the Shoko function is denoted as Shoka function:

\( \mathrm{Shoka}(z)=x+\ln\!\Big( \exp(-z) +\mathrm e -1\Big)\)

Complex map of the Shoka function is shorm in figure at right.

For moderate values of the imaginary part of the argument, say, \(|\Im(z)|<\pi\), the Shoka function coincide with the Shoko function, \(\mathrm{Shoko}(z)=\mathrm{Shoka}(z)\).

The Shoka function has the same branchpoints as the Shoko function, and the set of cutlines are shown in the figure, \( x \le r\), \(y= \mathrm (1+2n) \mathrm i \pi\) for integer \(n\).

Two of the cutlines look similar to the cutlines of the Tania function. However, the countable set of cutlines of the Shoka function makes the qualitative difference between the Shoka function and the Tania function, which has only two cutlines.

The price for orienting of cutlines to the left happened to be the loss of periodicity. For this reason, it is difficult to choose, which of functions, Shoko or Shoka should be considered as the "main", "prncipal", in order to treat another one as the the "modification", alternative.

While the imaginary part of the argument is not too latge, say, \(|\Im(z)<4\), functions \(\mathrm{Shoka}(z)\) and \(\mathrm{Tania}(z)\) look similar. At larger values of the imaginary part, and negative values of \(\Re(z)\), the deviation becomes qualitative; the Shoka function has countable set of cutlines, while the Tania function has only two.

The holomorphic extension of superfunctions may be important tool of analysis of the transfer functions of the laser amplifiers. The only pair of the cutlines correspond to the medium with fast response (or amplification of a long pulse), id est, the continuous or quasi–continuous operation. The countable set of the cut lines correspond to the medium with slow response (or amplification of a short pulse), id est, the pulsed operation. This hypothesis could be tested with the precise measurement of the transfer functions of the realistic amplifiers and numerical analysis of the corresponding superfunctions.

Shoko function as superfunction

The Shoko function appears at the regular iteration with the Keller function as the transfer function

\( \!\!\!\!\!\!\!\!\!\! (5) ~ ~ ~ T(z)=\mathrm {Keller}(z)=\ln\Big(1+\mathrm e \,(\mathrm e^z-1)\Big)\)

at its fixed point \(L\!=\!0\).

The \(c\)th iteration of the Keller function can be expressed through the Shoko function as usually;

\( \!\!\!\!\!\!\!\!\!\! (6) ~ ~ ~ T^c(z)=\mathrm {Keller}^c(z)= \mathrm{Shoko}\Big(c+\mathrm{ArcShoko}(z)\Big) = \ln\!\Big(1+\mathrm e^c(\mathrm e^z\!-\!1)\Big) \)

Inverse function

As the argument of the Shoko function is used in (1) only once, the calculation of the inverse function is straightforward:

\(\!\!\!\!\!\!\!\!\!\! (7) ~ ~ ~ \displaystyle \mathrm{ArcShoko}(z)=\mathrm{Shoko}^{-1}(z)=\ln \left( \frac{\mathrm e^z -1}{\mathrm e - 1} \right) \)

The simple representation agrees with the specific values of the Shoko and ArcShoko functions:

\(\!\!\!\!\!\!\!\!\!\! (8) ~ ~ ~ \mathrm{Shoko}(0)=1~\); \(~ ~\mathrm{ArcShoko}(1)=0\)

Application of Shoko function

Copmarison of the Shoko function (thick curve) to the Tania function (thin curve)

The Shoko function appears at the consideration of propagation of short pulse in laser amplifier with simple kinetics of the laser medium.

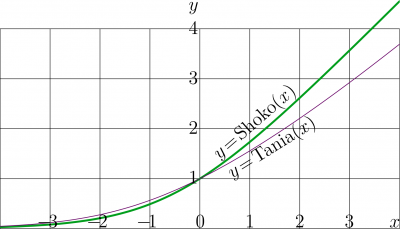
The Shoko function is analogy of the Tania function, that describes the propagation of the continuous wave in the amplifier with permanent continuous pump, with the same simple kinetics. Both Shoko function and Tania function are plotted in the figure at right. Both curves, for Tania and for Shoko, show similar behavior, exponential growth in the left hand side, that gradually changes to the almost linear growth in the right hand side; but the Shoko function grows a little bit faster than the Tania function.

in TORI, the Keller function is used as an example of the transfer function, for which the superfunction can be constructed as elementary finction, and the Shoko function is this function.

The argument of the Shoko function may have sense of the distance of propagation of a pulse in the gain medium, normalized for the inverse of the gain of a weak signal. Then the Shoko function returns the fluence at this distance, normalized for the saturation fluence.

While the fluence is small, it grows exponentially, according the the asymptotic (2).

The origin of coordinate along the direction of propagation is choosen in such a way, that \(\mathrm{Shoko}(0)=1\), which corresponds to the fluence equal to the saturation fluence.

At large values of fluence, it withdraws almost all the energy, stored in the gain medium, and, therefore, the growth is almost linear, according to the asymptotic (4).

Origin of the name

Shoko had strongly pressed the Editor to work as hard as a horse (see figure at right), in order to apply the formalism of superfunctions to the laser science. Then Yulya helped to find the literature, where the simple model of laser medium is used to describe the growth of the fluence of a pulse during the amplification; this growth can be expressed with function (1). As the name Yulya function already has been occupied (denoting the dependence that appears in the interferometric microscopy), the function (1) is named after Shoko (with her permission).

However, the colleagues who specialize in history of science may find that another name to be more suitable for function (1). Then they are cordially invited to describe the properties and applications of this function under that another (more suitable) name and send the link to the Editor of TORI, in order to cite it in this article.

Keywords

Superfunction, Regular iteration, Keller function, Elementary function, Holomorphic function, Laser science