Difference between revisions of "Stirling"
(Created page with "{{top}} Stirling («Stirling's Approximation», StirlingsApproximation <ref>https://mathworld.wolfram.com/StirlingsApproximation.html Stirling's approximation gives an...") |
m (principal branch) |
||
| Line 72: | Line 72: | ||
Here symbol [[Bernoulli]] denotes the [[Bernoulli number]], |
Here symbol [[Bernoulli]] denotes the [[Bernoulli number]], |
||
https://dlmf.nist.gov/24.2#i |
https://dlmf.nist.gov/24.2#i |
||
| + | |||
| + | For complex \(z\), [[LoGamma]]\(x\) denotes the principal branch of \(\log\Gamma(z)\). |
||
| + | In general, the multivalued functions are not considered in [[TORI]]; |
||
| + | if a need to refer to another branch, that branch is given a new name. |
||
At \(x>0\), the simple relation holds: \(\mathrm{LoGamma}(x)=\ln(\Gamma(x)) \ \). |
At \(x>0\), the simple relation holds: \(\mathrm{LoGamma}(x)=\ln(\Gamma(x)) \ \). |
||
In wide range of \(z\), the inverse relation is valid: \(\ \Gamma(z) = \exp(\mathrm{LoGamma}(z))\ \). |
In wide range of \(z\), the inverse relation is valid: \(\ \Gamma(z) = \exp(\mathrm{LoGamma}(z))\ \). |
||
| + | |||
For [[Gamma function]], the expansion is written as follows |
For [[Gamma function]], the expansion is written as follows |
||
Revision as of 16:54, 22 January 2026
Stirling («Stirling's Approximation», StirlingsApproximation [1], «Stirling expansion» [2], «スターリングの近似»[3], «Формула Стирлинга»[4]) refers to the set of asymptotics of Factorial and/or Gamma function at large values: \[ z!= \mathrm{Factorial}(z) \sim \sqrt{2\pi z}\ \exp\left(\log\left(\frac{z}{\mathrm e} \right) z \right) \] Various versions of this formula are collected in this article.
Factorial and Gamma function
The Stirling asymptotic refers to the Factorial and the Gamma function.
These two functions are connected with the displacement of the argument: \[ \Gamma(z)=\mathrm{Factorial}(z-1) \] For \(\ \Re(z)\ge 0 \ \), Factorial\(z\) can be defined (and evaluated) through the integral, \[ z! = \int_0^\infty t^z \exp(-t) \mathrm{d}t \] For other values, formula \[ z!\ (-z)! =\frac{\pi z}{\sin(\pi z)} \] can be used. This integral representation is not efficient at large \(|z|\); so, the Stirling is a good tool to cover all the complex plane with the precise approximations.
Historically, at TORI, the Factorial and its derivative had been implemented first for evaluation of ArcFactorial, SuperFactorial, AbelFactorial, Square root of factorial and other non-integer iterates of Factorial [5], 2010.
To year 2026, the fac.cin remains the best (robust, precise, fast) complex double implementation of Factorial available in the free access.
(The same refer also to the TORI implementations of functions ArcFactorial, SuperFactorial, AbelFactorial, the Natural tetration and some other superfunctions[6][7], 2014-2020).
Here, the Gamma function is implemented through Factorial.
For this reason Factorial appears in the right hand side of the first equation above;
the Gamma function is programmed so in the generators of the figures.
Usually, the Factorial is implemented through the Gamma function, and it is written as follows:
\(\ z! \!=\!\Gamma(z\!+\!1)\ \).
Editor hopes, any colleague can easy swap the right and left sides of the First equation and replace \(z\) to \(\ z\!+\!1 \ \), bringing that equation to the usual form. This may have sense if the colleague already has the efficient implementation of Gamma function that does not use its expression through Factorial.
Gamma function and LoGamma
The DLMF [8] (Digital Library of Mathematical Functions, https://dlmf.nist.gov/5.11#i) suggests the expansion for the LoGamma function as follows: \[ \mathrm{LoGamma}(z) \sim \left(z-\frac{1}{2}\right) \ln(z)-z+\frac{1}{2}\ln(2\pi)+ \sum_{k=0}^\infty \frac{\mathrm{Bernoulli}_{2k}}{2k(2k-1) z^{2k-1}} \] Here symbol Bernoulli denotes the Bernoulli number, https://dlmf.nist.gov/24.2#i
For complex \(z\), LoGamma\(x\) denotes the principal branch of \(\log\Gamma(z)\). In general, the multivalued functions are not considered in TORI; if a need to refer to another branch, that branch is given a new name.
At \(x>0\), the simple relation holds: \(\mathrm{LoGamma}(x)=\ln(\Gamma(x)) \ \).
In wide range of \(z\), the inverse relation is valid: \(\ \Gamma(z) = \exp(\mathrm{LoGamma}(z))\ \).
For Gamma function, the expansion is written as follows
\[
\Gamma(z) \sim
\mathrm e^{-z} z^z \left(\frac{2\pi}{z}\right)^{1/2} \sum_{k=0}^\infty \frac{g_k}{z^k}
\]
\(g_0=1 \)
\(g_1=1 / 12 \)
\(g_2=1 / 288 \)
\(g_3=-139 / 51840 \)
\(g_4=-571 / 2488320 \)
\(g_5=163879 / 209018880 \)
\(g_6=5246819 / 75246796800 \)
The truncation of the formulas above give the restricted asymptotics of LoGamma and Gamma function.
These restricted asymptotics are approximations useful for the evaluation and the numerical impementation of these functions.
The restriction applies to vicility of negative part of the real axis; this refers to the sectorial asymptotic.
Factorial
The sectorial asymptotic for Factorial can be written as follows: \[ A(z)= \sqrt{2\pi z}\ \exp\left( z\log\frac{z}{\mathrm e} + \frac{1}{12 z} \left( 1 -\frac{1}{30z^2} +\frac{1}{105z^4} -\frac{1}{140z^6} +\frac{1}{99z^8} -\frac{691}{30030 z^{10}} \right) \right) \]
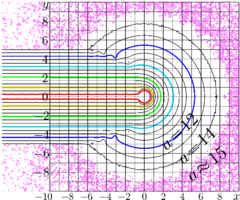
The figure at right shows the map of agreement \[ a(z) = - \lg \left(\frac{|z!-A(z)|}{|z!|+|A(z)|}\right). \] This agreement estimates, how may significant figures can one get with approximation \(A\).
The map of the agreement \(a\) suggests that the approximation \(A(z)\) provides of order of 14 decimal digits of Factorial\((z)\) in the range \[ d = (\ \Re(z) \!\ge\! -6 , \ |z|\!>\!8\ )\ \lor \ (\Re(z)\!<\!-6 , \ |\Im(z)|\!>\!5 \ )\!\!\!\!\!\! \]
Function \(A\) is interpreted as Restricted asymptotic:
It is the Sectorial asymptotic of Factorial at large values for sector
\(
D= \{ z\in \mathbf C \ : |\arg(z)|< \alpha \}
\);
here \(\alpha\) is any positive real number such that \( \alpha < \pi \).
At large \(|z|\),
the residual \(\ r(z)\!=\)Factorial\((z)\!-\!A(z) \ \)
remains asymptotically negligible compared to Factorial\((z)\)
in the whole complex \(z\) plane
except an arbitrarily narrow sector containing the negative real axis:
\[
\lim_{|z|\to \infty, \ z \in D} \frac{r(z)}{z!} = 0
\]
Here, the limit is not uniform as \(\alpha\to\pi\ \).
The mathematically precise version of the formula above can be written as follows:
\[
\forall \alpha<\pi:\quad
\lim_{|z|\to\infty,\ |\arg z|\le \alpha}
\frac{r(z)}{z!}=0
\]
In a little bit less efficient form, the asymptotic of Factorial for large values can be written as follows:
\(\displaystyle B(z)= \sqrt{2\pi z}\ \exp\left(\log\left(\frac{z}{\mathrm e} \right) z \right) \times\) \( \left(1+ \frac{1}{z}\left(\frac{1}{12}+ \frac{1}{z}\left(\frac{1}{288}+ \frac{1}{z}\left(\frac{-139}{51840}+ \frac{1}{z}\left(\frac{-571}{2488320}+ \frac{1}{z}\left(\frac{163879}{209018880}+ \frac{1}{z}\left(\frac{5246819}{75246796800} \right) \right) \right) \right) \right) \right)\right) \)
The coefficients in the truncated expansion coincide with coefficients \(g\) for the Gamma function above.
Function \(B\) also can be interpreted as Sectorial asymptotic of Factorial, with the same sector \(D\) as for asymptotic \(A\).
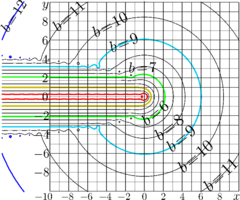
The second figure above shows the map of agreement
\[
b(z) = - \lg \left(\frac{|z!-B(z)|}{|z!|+|B(z)|}\right)
\]
in the same notations as the agreement \(a\) in the map in the figure above.
Attribution
ChatGPT helped to improve this article.
Routine «Conrec6.cin» by ChatGPT is used to plot the maps above.
References
- ↑ https://mathworld.wolfram.com/StirlingsApproximation.html Stirling's approximation gives an approximate value for the factorial function n! or the gamma function Gamma(n) for n>>1. ..
- ↑ https://hrcak.srce.hr/file/92599 Cristinel Mortici. On the stirling expansion into negative powers of a triangular number. Math. Commun., Vol. 15, No. 2, pp. 359-364 (2010).
- ↑ https://ja.wikipedia.org/wiki/スターリングの近似
- ↑ http://nuclphys.sinp.msu.ru/mathan/p3/m3205.html 32.5. Формула Стирлинга // Разложение функции ln(1+x) в степенной ряд дает возможность легко получить асимптотическую формулу для факториала n! .. Эта формула называется формулой Стирлинга;
- ↑
https://link.springer.com/article/10.3103/S0027134910010029
https://mizugadro.mydns.jp/PAPERS/2010superfae.pdf English version
https://mizugadro.mydns.jp/PAPERS/2010superfar.pdf Russian version
D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12. (Russian version: p.8-14) - ↑ https://mizugadro.myfns.jp/PAPERS/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014.
- ↑ https://mizugadro.myfns.jp/PAPERS/486.pdf D.Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.
- ↑ https://dlmf.nist.gov/5.11#i §5.11(i) Poincaré-Type Expansions
https://en.wikipedia.org/wiki/Factorial
https://en.wikipedia.org/wiki/Stirling%27s_approximation
https://en.citizendium.org/wiki/Factorial#Stirling's_formula
Keywords
«AbelFactorial», «ArcFactorial», «Agreement», «Approximation», «Asymptotic», «Bernoulli», «Gamma function», «Factorial», «fac.cin», «LoFac», «LoGamma», «Restricted asymptotic», «Sectorial asymptotic», «Stirling», «SuperFactorial», «Superfunctions»,
«Формула Стирлинга», «スターリングの近似»,