Difference between revisions of "Superfunction"
| (26 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | [[Superfunction]] comes from iteration of some function. |
|
| − | Roughly, for some function <math>T</math> (which is called [[Transfer function]]) and for some constant <math>t</math>, the superfunction $F$ could be defined with expression |
||
| + | For some function <math>T</math> (which is called [[Transfer function]]) and for some constant <math>t</math>, the superfunction \(F\) could be defined with expression |
||
| − | $\displaystyle {{F(z)} \atop \,} {= \atop \,} |
||
| + | |||
| + | \(\displaystyle {{F(z)} \atop \,} {= \atop \,} |
||
{T^z(t) \atop \,} {= \atop \,} |
{T^z(t) \atop \,} {= \atop \,} |
||
{{\underbrace{T\Big(T\big(... T(t)...\big)\Big)}} \atop {z \mathrm{~evaluations~of~function~}T\! |
{{\underbrace{T\Big(T\big(... T(t)...\big)\Big)}} \atop {z \mathrm{~evaluations~of~function~}T\! |
||
| − | \!\!\!\!\!}} |
+ | \!\!\!\!\!}}\) |
then <math>F</math> can be interpreted as superfunction of function <math>T</math>. |
then <math>F</math> can be interpreted as superfunction of function <math>T</math>. |
||
| Line 17: | Line 18: | ||
!--> |
!--> |
||
In particular, the [[Ackernann functions]] and [[tetration]] can be interpreted in terms of [[superfunction]]s. |
In particular, the [[Ackernann functions]] and [[tetration]] can be interpreted in terms of [[superfunction]]s. |
||
| + | <div style="float:right; margin:0px -14px 0px 8px"> |
||
| + | [[File:HellmuthKneserPhotoNormal.jpeg|190px]]<br><small><center> |
||
| + | [[Hellmuth Kneser]], 1958 <ref> |
||
| + | https://opc.mfo.de/detail?photo_id=7607 On the Photo: Kneser, Hellmuth Location: Oberwolfach Author: Danzer, Ludwig (photos provided by Danzer, Ludwig) Source: L. Danzer, Dortmund Year: 1958 Copyright: L. Danzer, Dortmund Photo ID: 7607 |
||
| + | </ref></center></small> |
||
| + | </div> |
||
==History== |
==History== |
||
| + | <div style="float:left;width:200px; margin:0px 6px 0px -170px"> |
||
| − | <!--[[Image:QFacQexp.jpg|right|600px|thumb|<math>\sqrt{!}</math> and <math>\sqrt{\exp}</math> in the complex plane]] |
||
| − | [[Image: |
+ | [[Image:Sqrt(factorial)LOGOintegralLOGO.jpg|200px]]<small> |
| − | + | logos of Phys. and Math. depts <!--of [[Moscow State University|MSU]]!--></small> |
|
| + | </div> |
||
| − | [[File:QexpMapT400.jpg|200px|thumb| $u+\mathrm i v=\sqrt{\exp} (x+\mathrm i y)$]] |
||
| + | <div style="float:right;margin:0px -14px 0px 8px"> |
||
| − | [[File:QfacMapT500a.jpg|200px|thumb| $u+\mathrm i v=\sqrt{!}(x+\mathrm i y)$]] |
||
| + | [[File:QexpMapT400.jpg|200px]]<br><small><center> \(u+\mathrm i v=\sqrt{\exp} (x+\mathrm i y)\)</center></small> |
||
| − | Analysis of superfunctions came from the application to the evaluation of fractional iterations of functions. |
||
| + | |||
| − | [[Superfunction]]s and their inverse functions ([[Abel function]]s) allow evaluation of not only minus-first power of a function (inverse function), but also any real and even complex [[iteration]] of the function. Historically, the first function of such kind considered was <math>\sqrt{\exp}~</math> |
||
| + | [[File:QfacMapT500a.jpg|200px]]<br><small><center> \(u+\mathrm i v=\sqrt{!}(x+\mathrm i y)\) |
||
| + | </div></center></small> |
||
| + | Analysis of superfunctions came from the application to the evaluation of fractional iterations of functions. |
||
| + | |||
| + | [[Superfunction]]s and their inverse functions ([[Abel function]]s) allow evaluation of not only minus-first power of a function (inverse function), but also any real and even complex [[iteration]] of the function. |
||
| + | |||
| + | Historically, the first function of such kind, iteration half of the exponential, id est, |
||
| + | <math>\sqrt{\exp}~</math>, is considered in 1950 by [[Hellmuth Kneser]] |
||
<ref name="kneser"> |
<ref name="kneser"> |
||
| − | http:// |
+ | http://mizugadro.mydns.jp/PAPERS/Relle.pdf |
[[Helmuth Kneser]] |
[[Helmuth Kneser]] |
||
Reelle analytische L¨osungen der Gleichung <math>\varphi(\varphi(x)) = e^x </math> und verwandter Funktionalgleichungen |
Reelle analytische L¨osungen der Gleichung <math>\varphi(\varphi(x)) = e^x </math> und verwandter Funktionalgleichungen |
||
[[Journal fur die reine und angewandte Mathematik]] '''187''' (1950) 56-67 |
[[Journal fur die reine und angewandte Mathematik]] '''187''' (1950) 56-67 |
||
| + | </ref>. That time, no algorithm had been suggested for evaluation of this function. |
||
| − | + | Since 1960, function <math>\sqrt{!~}~</math> is accepted as logo of the Physics department of the [[Moscow State University]], see the first picture of the figure at left. <br> |
|
| + | Until year 2007, this symbol is believed to have no mathematical sense |
||
| − | <ref name="logo">Logo of the Physics Department of the Moscow State University. (In Russian); |
||
| + | <ref name="kandidov"> |
||
| − | http://zhurnal.lib.ru/img/g/garik/dubinushka/index.shtml |
||
| + | V.P.Kandidov. About the time and myself. (In Russian) 2007.05.18. |
||
| − | </ref><ref name="kandidov"> |
||
| − | V.P.Kandidov. About the time and myself. (In Russian) |
||
http://ofvp.phys.msu.ru/pdf/Kandidov_70.pdf: |
http://ofvp.phys.msu.ru/pdf/Kandidov_70.pdf: |
||
| − | + | .. По итогам студенческого голосования победителями оказались значок с изображением |
|
рычага, поднимающего Землю, и нынешний с хорошо известной эмблемой в виде |
рычага, поднимающего Землю, и нынешний с хорошо известной эмблемой в виде |
||
корня из факториала, вписанными в букву Ф. Этот значок, созданный студентом |
корня из факториала, вписанными в букву Ф. Этот значок, созданный студентом |
||
| Line 44: | Line 59: | ||
выразительностью. Тогда эмблема этого значка подверглась жесткой критике со |
выразительностью. Тогда эмблема этого значка подверглась жесткой критике со |
||
стороны руководства факультета, поскольку она не имеет физического смысла, |
стороны руководства факультета, поскольку она не имеет физического смысла, |
||
| − | математически абсурдна и идеологически бессодержательна. |
+ | математически абсурдна и идеологически бессодержательна. .. |
| − | </blockquote> |
||
</ref><ref name="naukai"> |
</ref><ref name="naukai"> |
||
| + | https://www.nkj.ru/archive/articles/1023/ |
||
| − | 250 anniversary of the Moscow State University. (In Russian) |
||
| + | V.Sadovnichi. 250 anniversary of the Moscow State University. (In Russian) |
||
| − | ПЕРВОМУ УНИВЕРСИТЕТУ СТРАНЫ - 250! |
||
| + | В. Садовничий. ПЕРВОМУ УНИВЕРСИТЕТУ СТРАНЫ - 250! НАУКА И ЖИЗНЬ, №1, 2005. |
||
| − | http://nauka.relis.ru/11/0412/11412002.htm |
||
| + | .. На значке физфака в букву "Ф" вписано стилизованное изображение корня из факториала (√!) - выражение, математического смысла не имеющее. ..</ref><ref name="logo">Logo of the Physics Department of the Moscow State University. (In Russian); |
||
| − | <blockquote> |
||
| + | http://zhurnal.lib.ru/img/g/garik/dubinushka/index.shtml |
||
| − | На значке физфака в букву "Ф" вписано стилизованное изображение корня из факториала (√!) - выражение, математического смысла не имеющее. |
||
| − | </ |
+ | </ref>. |
| + | |||
| − | </ref>. The [[complex map]]s of these functions are shown in figures at right. |
||
| + | The [[complex map]]s of functions \( \sqrt{\exp} \) and \(\sqrt{!} \) are shown in figures at right. |
||
| − | Mathematicians of the same University were not so arrogant and used the symbol of [[integral]] and the [[Moebius surface]] at their logo, see the figure at right. |
||
| + | |||
| + | Mathematicians of the same University were not so arrogant and used the symbol of [[integral]] and the [[Moebius surface]] at their logo, see second picture of the figure at left. |
||
That time, researchers did not have computational facilities for evaluation of such functions, but |
That time, researchers did not have computational facilities for evaluation of such functions, but |
||
the <math>\sqrt{\exp}</math> was more lucky than the <math>~\sqrt{!~}~~</math>; at least the existence of [[holomorphic function]] |
the <math>\sqrt{\exp}</math> was more lucky than the <math>~\sqrt{!~}~~</math>; at least the existence of [[holomorphic function]] |
||
| − | <math>\varphi</math> such that <math>\varphi(\varphi(z))=\exp(z)</math> has been |
+ | <math>\varphi</math> such that <math>\varphi(\varphi(z))=\exp(z)</math> has been declared <ref name="kneser"/>. Actually, for his proof, Kneser had constructed the [[superfunction]] of exp and corresponding [[Abel function]] <math>\mathcal{X}</math>, satisfying the [[Abel equation]] |
| − | http://tori.ils.uec.ac.jp/PAPERS/Relle.pdf |
||
| − | H.Kneser. |
||
| − | Reelle analytische Lösungen der Gleichung <math>\varphi(\varphi(x)) = e^x </math> und verwandter Funktionalgleichungen. |
||
| − | Journal fur die reine und angewandte Mathematik |
||
| − | '''187''' (1950) |
||
| − | </ref>. Actually, for his proof, Kneser had constructed the [[superfunction]] of exp and corresponding [[Abel function]] <math>\mathcal{X}</math>, satisfying the [[Abel equation]] |
||
: <math>\mathcal{X}(\exp(z))=\mathcal{X}(z)+1</math> . |
: <math>\mathcal{X}(\exp(z))=\mathcal{X}(z)+1</math> . |
||
The [[inverse function]], id est <math>F=\mathcal \chi^{-1}</math> is an [[entire function|entire]] super-exponential, although it is not real at the real axis; it cannot be interpreted as [[tetration]], because the condition <math>F(0)=1</math> cannot be realized for the entire super-exponential. The [[real function|real]] <math>\sqrt{\exp}</math> can be constructed with the [[tetration]] (which is also a superexponential), and the real <math>\sqrt{\rm Factorial}</math> can be constructed with the [[SuperFactorial]]. The plots of <math>\sqrt{\rm Factorial}~</math> and <math>\sqrt{\exp}~</math> in the compex plane are shown in the right hand side figure. |
The [[inverse function]], id est <math>F=\mathcal \chi^{-1}</math> is an [[entire function|entire]] super-exponential, although it is not real at the real axis; it cannot be interpreted as [[tetration]], because the condition <math>F(0)=1</math> cannot be realized for the entire super-exponential. The [[real function|real]] <math>\sqrt{\exp}</math> can be constructed with the [[tetration]] (which is also a superexponential), and the real <math>\sqrt{\rm Factorial}</math> can be constructed with the [[SuperFactorial]]. The plots of <math>\sqrt{\rm Factorial}~</math> and <math>\sqrt{\exp}~</math> in the compex plane are shown in the right hand side figure. |
||
| Line 71: | Line 81: | ||
The recurrent formula of the preamble can be written as equations |
The recurrent formula of the preamble can be written as equations |
||
| − | + | \(F(z\!+\!1)=T(F(z)) ~ \forall z\in \mathbb{N} : z>0\) |
|
| − | + | \(F(1)=t\) |
|
Instead of the last equation, one could write |
Instead of the last equation, one could write |
||
| − | + | \(F(0)=t\) |
|
and extend the range of definition of superfunction <math>F</math> to the non-negative integers. Then, one may postulate |
and extend the range of definition of superfunction <math>F</math> to the non-negative integers. Then, one may postulate |
||
| − | + | \(F(-1)=T^{-1}(t)\) |
|
and extend the range of validity to the negative integer values, at least while the inverse of the Transfer function is holomorphic. |
and extend the range of validity to the negative integer values, at least while the inverse of the Transfer function is holomorphic. |
||
For example, |
For example, |
||
| − | + | \(F(-2)=T^{-2}(t)=T^{-1}\Big(T^{-1}(t)\Big)\) |
|
and so on. However, the inverse function may happen to be not defined for some values of <math>t</math>. |
and so on. However, the inverse function may happen to be not defined for some values of <math>t</math>. |
||
| Line 92: | Line 102: | ||
The [[tetration]] is considered as super-function of exponential for some real base <math>b</math>; in this case, |
The [[tetration]] is considered as super-function of exponential for some real base <math>b</math>; in this case, |
||
| − | + | \(T=\exp_{b}\) |
|
| − | then, at |
+ | then, at \(t=1\), |
| − | + | \(F(-1)=\log_b(1)=0 ~ ~, ~ ~ \mathrm{but}\) |
|
| − | + | \(F(-2)=\log_b(0)~ \mathrm{~is~ not~ defined}\) |
|
For extension to non-integer values of the argument, superfunction should be defined in different way. |
For extension to non-integer values of the argument, superfunction should be defined in different way. |
||
| Line 108: | Line 118: | ||
function <math> F </math>, [[holomorphic]] on domain <math>D</math>, such that |
function <math> F </math>, [[holomorphic]] on domain <math>D</math>, such that |
||
| − | + | \(F(z\!+\!1)=T(F(z)) ~ \forall z\in D : z\!+\!1 \in D\) |
|
| − | + | \(F(p)=q\) |
|
==Uniqueness== |
==Uniqueness== |
||
In general, the super-function is not unique. |
In general, the super-function is not unique. |
||
| − | For a given base function <math>T</math>, from given <math>(p\mapsto q)</math> |
+ | For a given base function <math>T</math>, from given <math>(p\mapsto q)</math> superfunction <math>F</math>, another <math>(p \mapsto q)</math> superfunction <math>\tilde F</math> could be constructed as |
: <math>\tilde F(z)=F(z+\mu(z))</math> |
: <math>\tilde F(z)=F(z+\mu(z))</math> |
||
where <math>\mu</math> is any 1-periodic function, holomorphic at least in some vicinity of the real axis, such that <math> \mu(p)=0 </math>. |
where <math>\mu</math> is any 1-periodic function, holomorphic at least in some vicinity of the real axis, such that <math> \mu(p)=0 </math>. |
||
| Line 169: | Line 179: | ||
===Quadratic polynomials=== |
===Quadratic polynomials=== |
||
| − | Let the transfer |
+ | Let the transfer function \(T\) be defined with \(T(z)=2 z^2-1\). |
Then, |
Then, |
||
| − | + | \(F(z)=\cos( \pi \cdot 2^z) \) is a |
|
| − | + | \((\mathbb{C},~ 0\! \rightarrow\! 1)\) superfunction of \(T\). |
|
Indeed, |
Indeed, |
||
| − | + | \(F(z\!+\!1)=\cos(2 \pi \cdot 2^z)=2\cos(\pi \cdot 2^z)^2 -1 =T(F(z))\) |
|
and |
and |
||
| − | + | \(F(0)=\cos(2\pi)=1\) |
|
| − | In this case, the superfunction |
+ | In this case, the superfunction \(F\) is periodic; its period |
| − | + | \(\tau=\frac{2\pi}{\ln(2)} \mathrm{i}\approx 9.0647202836543876194 \!~i \) |
|
and the superfunction approaches unity also in the negative direction of the real axis, |
and the superfunction approaches unity also in the negative direction of the real axis, |
||
| − | + | \(\lim_{x\rightarrow -\infty} F(x)=1\) |
|
The example above and the two examples below are suggested at |
The example above and the two examples below are suggested at |
||
<ref name="mueller">Mueller. Problems in Mathematics. http://www.math.tu-berlin.de/~mueller/projects.html </ref> |
<ref name="mueller">Mueller. Problems in Mathematics. http://www.math.tu-berlin.de/~mueller/projects.html </ref> |
||
| − | In general, the transfer function |
+ | In general, the transfer function \(T\) has no need to be [[entire function]]. |
| − | Here is the example with [[meromorphic function]] |
+ | Here is the example with [[meromorphic function]] \(T\). |
Let |
Let |
||
| − | + | \(T(z)=\frac{2z}{1-z^2} ~ \forall z\in D~\); \(~ D=\mathbb{C} \backslash \{-1,1\}\) |
|
Then, function |
Then, function |
||
| − | + | \(F(z)=\tan(\pi 2^z)\) |
|
| − | is |
+ | is \((C, 0\! \mapsto\! 0)\) superfunction of function \(T\), where |
| − | + | \(C\) is the set of complex numbers except singularities of function \(F\). |
|
For the proof, the trigonometric formula |
For the proof, the trigonometric formula |
||
| − | + | \(\displaystyle |
|
\tan(2 \alpha)=\frac{2 \tan(\alpha)}{1-\tan(\alpha)^2}~~ |
\tan(2 \alpha)=\frac{2 \tan(\alpha)}{1-\tan(\alpha)^2}~~ |
||
\forall \alpha \in \mathbb{C} \backslash \{\alpha\in \mathbb{C} : \cos(\alpha)=0 || \sin(\alpha)=\pm \cos(\alpha) \} |
\forall \alpha \in \mathbb{C} \backslash \{\alpha\in \mathbb{C} : \cos(\alpha)=0 || \sin(\alpha)=\pm \cos(\alpha) \} |
||
| + | \) |
||
| − | $ |
||
can be used at <math>\alpha=\pi 2^z </math>, that gives |
can be used at <math>\alpha=\pi 2^z </math>, that gives |
||
| − | + | \(\displaystyle |
|
| − | T(F(z))=\frac{2 \tan(\pi 2^z)}{1-\tan(\pi 2^z)} = \tan(2 \pi 2^z)=F(z+1) |
+ | T(F(z))=\frac{2 \tan(\pi 2^z)}{1-\tan(\pi 2^z)} = \tan(2 \pi 2^z)=F(z+1)\) |
<!-- However, such function <math>F(z)</math> allows the holomrphic extension to values, where <math>cos(\pi 2^z)=0</math>, |
<!-- However, such function <math>F(z)</math> allows the holomrphic extension to values, where <math>cos(\pi 2^z)=0</math>, |
||
setting it to zero in these points, but it has singularities, poles, at <math>2^z=\frac{1+2n}{4}</math> for integer <math>n</math>. |
setting it to zero in these points, but it has singularities, poles, at <math>2^z=\frac{1+2n}{4}</math> for integer <math>n</math>. |
||
| Line 221: | Line 231: | ||
In the similar way one can consider the transfer function |
In the similar way one can consider the transfer function |
||
| − | + | \(T(z)=2z \sqrt{1-z^2}\) |
|
and |
and |
||
| − | + | \(F(z)=\sin(\pi 2^z)\) |
|
| − | which is |
+ | which is \((C,~ 0\!\rightarrow \!0)\) superfunction of \(H\) for |
| − | + | \(C= \{z\in \mathbb C : \Re( \cos(\pi 2^z))>0 \}\). |
|
===Exponentiation=== |
===Exponentiation=== |
||
| Line 239: | Line 249: | ||
==Abel function== |
==Abel function== |
||
| − | Inverse of superfunction |
+ | Inverse of superfunction \(G=F^{-1}\) is called the [[Abel function]]; within some domain, it satisfies the Abel equation |
| − | + | \(T(G(z))=G(z)+1\) |
|
==Applications of superfunctions and the Abel functions== |
==Applications of superfunctions and the Abel functions== |
||
| Line 253: | Line 263: | ||
corresponding Abel functions can be considered. |
corresponding Abel functions can be considered. |
||
===Nest=== |
===Nest=== |
||
| − | The |
+ | The \(c\)th iteration of some function \(f\) can be expressed through the [[superfunction]] \(F\) and the [[Abel function]] \(G=F^{-1}\): |
| − | : |
+ | :\( T^c(z)=F(c+G(z))\) |
In [[Mathematica]], there already exist the special name for the operation, that could evaluate such a expression. It is called [[Nest]]. |
In [[Mathematica]], there already exist the special name for the operation, that could evaluate such a expression. It is called [[Nest]]. |
||
<ref name="nest"> |
<ref name="nest"> |
||
| Line 262: | Line 272: | ||
The second argument indicates the initial value. |
The second argument indicates the initial value. |
||
The third (and last) argument indicates the number of iterations. |
The third (and last) argument indicates the number of iterations. |
||
| − | Then, the iteration of function |
+ | Then, the iteration of function \(T\) can be written as follows: |
| − | : |
+ | :\( T^c(z)=\mathrm {Nest}[T,z,c]\) |
Unfortunately, in the version "Mathematica 8", the implementation of the [[Nest]] has serious restrictions: the number of iterations should allow the simplification to an integer constant. |
Unfortunately, in the version "Mathematica 8", the implementation of the [[Nest]] has serious restrictions: the number of iterations should allow the simplification to an integer constant. |
||
| Line 276: | Line 286: | ||
===Transition from a function to its inverse function=== |
===Transition from a function to its inverse function=== |
||
| + | <div style="float:left;width:1px"> |
||
| − | [[Image:Expc.jpg|200px|left|thumb|<math>\exp^c(x)</math> versus <math>x</math> for various <math>c</math>]] |
||
| + | <div style="float:right;width:184px"> |
||
| − | [[Image:Sqrt(exp)(z).jpg|600px|right|thumb|<math>\exp^c</math> in the complex plane for various <math>c</math>]] |
||
| + | [[Image:Expc.jpg|180px]]<small><math>\exp^c(x)</math> versus <math>x</math> for various <math>c</math></small> |
||
| + | </div></div> |
||
| + | <div style="float:right;width:480px"> |
||
| + | <div style="width:500px"> |
||
| + | [[Image:Sqrt(exp)(z).jpg|500px]] |
||
| + | <math>\exp^c</math> in the complex plane for various <math>c</math> |
||
| + | </div></div> |
||
A [[superfunction]] <math>S</math> allows to calculate the fractional [[iteration]] <math>H^c</math> of some transfer function <math>H</math>. Once the superfunction <math>S</math> and the [[Abel function]] <math>A=S^{-1}</math> are established, |
A [[superfunction]] <math>S</math> allows to calculate the fractional [[iteration]] <math>H^c</math> of some transfer function <math>H</math>. Once the superfunction <math>S</math> and the [[Abel function]] <math>A=S^{-1}</math> are established, |
||
| Line 304: | Line 321: | ||
could be interpreted as the square root (id est, half-iteration) of the Transfer Function of the initial sample. |
could be interpreted as the square root (id est, half-iteration) of the Transfer Function of the initial sample. |
||
| − | Similar example is suggested for a nonlinear optical fiber |
+ | Similar example is suggested for a nonlinear optical fiber |
| + | <ref name="kouznetsov"> |
||
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html |
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html |
||
(preprint: http://www.ils.uec.ac.jp/~dima/PAPERS/analuxp99.pdf ) |
(preprint: http://www.ils.uec.ac.jp/~dima/PAPERS/analuxp99.pdf ) |
||
D.Kouznetsov. |
D.Kouznetsov. |
||
Solutions of <math>F(z+1)=\exp(F(z))</math> in the complex <math>z</math>plane. |
Solutions of <math>F(z+1)=\exp(F(z))</math> in the complex <math>z</math>plane. |
||
| − | [[Mathematics of Computation]], |
+ | [[Mathematics of Computation]], |
| + | '''78''' (2009) 1647-1670 |
||
| − | <!--doi=10.1090/S0025-5718-09-02188-7!--> |
||
| + | <!--10.1090/S0025-5718-09-02188-7!--> |
||
</ref>. |
</ref>. |
||
In particular, the [[Tania function]] can be evaluated using the [[Doya function]] and the [[regular iteration]] |
In particular, the [[Tania function]] can be evaluated using the [[Doya function]] and the [[regular iteration]] |
||
| Line 317: | Line 336: | ||
Dmitrii Kouznetsov. Superfunctions for amplifiers. Optical Review, July 2013, Volume 20, Issue 4, pp 321-326. |
Dmitrii Kouznetsov. Superfunctions for amplifiers. Optical Review, July 2013, Volume 20, Issue 4, pp 321-326. |
||
Preprint: http://mizugadro.mydns.jp/PAPERS/2013orSuper.pdf |
Preprint: http://mizugadro.mydns.jp/PAPERS/2013orSuper.pdf |
||
| − | </ref><ref name="sinapo"> |
+ | </ref><!--<ref name="sinapo"> http://mizugadro.mydns.jp/PAPERS/2011singapo.pdf |
| + | D.Kouznetsov. Transfer function of an amplifier and characterization of Materials. Singapore, 2011. (slideshow)</ref>!--> |
||
| − | http://www.ils.uec.ac.jp/~dima/PAPERS/2011singapo.pdf |
||
| + | at the fixed point \(0\), as \(\mathrm{Doya}_t(0)\!=\!0\). The same method can be applied also to other [[transfer function]]s, even if they cannot be easy represented through the [[special function]]s. This may refer, for example, to the experimentally–measured transfer function, that has no need to coincide with the [[Doya function]]. |
||
| − | http://mizugadro.mydns.jp/PAPERS/2011singapo.pdf |
||
| − | D.Kouznetsov. Transfer function of an amplifier and characterization of Materials. Singapore, 2011. |
||
| − | </ref> |
||
| − | at the fixed point $0$, as $\mathrm{Doya}_t(0)\!=\!0$. The same method can be applied also to other [[transfer funciton]]s, even if they cannot be easy represented through the [[special function]]s. This may refer, for example, to the experimentally–measured transfer function, that has no need to coincide with the [[Doya function]]. |
||
===Nonlinear Acoustics=== |
===Nonlinear Acoustics=== |
||
| Line 353: | Line 369: | ||
The operational element may have any origin: it can be realized as an electronic microchip, |
The operational element may have any origin: it can be realized as an electronic microchip, |
||
or a mechanical couple of curvilinear grains), or some asymmetric U-tube filled with different liquids, and so on. |
or a mechanical couple of curvilinear grains), or some asymmetric U-tube filled with different liquids, and so on. |
||
| + | |||
| + | ==Other meanings of words== |
||
| + | <div style="float:left;width:390px;margin:0px 16px 0px -178px"> |
||
| + | [[File:Superfunction icon.jpg|220px]] |
||
| + | [[File:Nestbird1.png|80px]] |
||
| + | [[File:107253 original.jpg|80px]]<small> |
||
| + | Not all [[superfunction]]s are holomorphic <ref> |
||
| + | https://endless-sport.co.jp/products/suspension/index_superfunction.html Functionメーカー別適合表 ホーム> サスペンショントップ Super Function / スーパーファンクション(サーキット向け)(2020). |
||
| + | </ref><ref> |
||
| + | https://www.pythonforbeginners.com/super/working-python-super-function |
||
| + | Working with the Python Super Function. |
||
| + | Last Updated: May 20, 2020. |
||
| + | Python 2.2 saw the introduction of a built-in function called “super,” which returns a proxy object to delegate method calls to a class – which can be either parent or sibling in nature. <!-- |
||
| + | That description may not make sense unless you have experience working with Python, so we’ll break it down. |
||
| + | Essentially, the super function can be used to gain access to inherited methods – from a parent or sibling class – that has been overwritten in a class object.!--> |
||
| + | </ref>; [[Nest]]; [[Superpower]]</small></div> |
||
| + | |||
| + | In mathematics, terms often have meaning, slightly deviating from terminology, used by the normal people. |
||
| + | |||
| + | Not all supperfunctions are holomorphic. |
||
| + | [[Nest]] may be difficult to implement in [[Mathematica]]. |
||
| + | Even term [[Superpower]] may have different meaning. |
||
==References== |
==References== |
||
<references/> |
<references/> |
||
| + | |||
| + | 2014. https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 |
||
| + | Dmitrii Kouznetsov. Суперфункции. Lambert Academic Publishing, 2014. (In Russian) |
||
| + | |||
| + | 2016. |
||
| + | https://doi.org/10.11568/kjm.2016.24.1.81 |
||
| + | W.Paulsen, “FINDING THE NATURAL SOLUTION TO f(f(x)) = exp(x),” Korean Journal of Mathematics, vol. 24, no. 1, pp. 81–106, Mar. 2016. |
||
| + | |||
| + | 2017. |
||
| + | https://search.proquest.com/openview/cb7af40083915e275005ffca4bfd4685/1 |
||
| + | S.Cowgill. Exploring Tetration in the Complex Plane. |
||
| + | Arkansas State University, ProQuest Dissertations Publishing, 2017. 10263680. |
||
| + | |||
| + | 2017. |
||
| + | https://doi.org/10.1007/s10444-017-9524-1 |
||
| + | W.Paulsen, S.Cowgill, Solving F(z + 1) = b ^ F(z) in the complex plane. Adv Comput Math 43, 1261–1282 (2017). |
||
| + | |||
| + | 2018. |
||
| + | https://doi.org/10.1080/10236198.2017.1307350 |
||
| + | M.H. Hooshmand. (2018) Ultra power of higher orders and ultra exponential functional sequences. Journal of Difference Equations and Applications. |
||
| + | Volume 24, 2018 - Issue 5: Special Issue: European Conference on Iteration Theory 2016. Special Issue Editors: Marek Cezary Zdun & Jaroslav Smital. |
||
| + | |||
| + | 2019. |
||
| + | https://doi.org/10.1007/s10444-018-9615-7 |
||
| + | W.Paulsen. Tetration for complex bases. Adv Comput Math 45, 243–267 (2019). |
||
| + | |||
| + | 2020. |
||
| + | https://www.morebooks.de/store/gb/book/superfunctions/isbn/978-620-2-67286-3 |
||
| + | D.Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020. |
||
| + | |||
| + | 2021. |
||
| + | https://arxiv.org/abs/2101.03021v2 |
||
| + | James David Nixon. Hyper-operations By Unconventional Means. March 8, 2021 |
||
==Keywords== |
==Keywords== |
||
| − | [[Transfer function]], |
||
| − | [[Transfer equation]], |
||
[[Abel function]], |
[[Abel function]], |
||
| − | [[Tetration]], |
||
| − | [[Superfactorial]], |
||
| − | [[Tania function]], |
||
[[Iteration]], |
[[Iteration]], |
||
[[Regular iteration]], |
[[Regular iteration]], |
||
[[SuperFactorial]], |
[[SuperFactorial]], |
||
| + | [[Superfunctions]], |
||
| + | [[Transfer function]], |
||
| + | [[Transfer equation]], |
||
| + | [[Tetration]], |
||
| + | [[Tania function]], |
||
[[Tania function]], |
[[Tania function]], |
||
[[Shoka function]], |
[[Shoka function]], |
||
[[SuZex]], |
[[SuZex]], |
||
[[SuTra]] |
[[SuTra]] |
||
| + | |||
| + | [[Суперфункции]] |
||
===Additional links=== |
===Additional links=== |
||
| Line 378: | Line 451: | ||
http://en.citizendium.org/wiki/Superfunction |
http://en.citizendium.org/wiki/Superfunction |
||
| − | [[Category: |
+ | [[Category:English]] |
| + | [[Category:Iterate]] |
||
| + | [[Category:Iteration]] |
||
[[Category:Mathematics]] |
[[Category:Mathematics]] |
||
| − | [[Category: |
+ | [[Category:Superfunction]] |
| + | [[Category:Superfunctions]] |
||
Latest revision as of 08:35, 3 May 2021
Superfunction comes from iteration of some function.
For some function \(T\) (which is called Transfer function) and for some constant \(t\), the superfunction \(F\) could be defined with expression
\(\displaystyle {{F(z)} \atop \,} {= \atop \,} {T^z(t) \atop \,} {= \atop \,} {{\underbrace{T\Big(T\big(... T(t)...\big)\Big)}} \atop {z \mathrm{~evaluations~of~function~}T\! \!\!\!\!\!}}\)
then \(F\) can be interpreted as superfunction of function \(T\). Such definition is valid only for positive integer \(z\). The most research and appllications around the superfunctions are related with various extensions of superfunction; and analysis of the existence, uniqueness and ways of the evaluation. For simple function \(T\), such as addition of a constant or multiplication by a constant, the superfunction can be expressed in terms of elementary function. In particular, the Ackernann functions and tetration can be interpreted in terms of superfunctions.
History
Analysis of superfunctions came from the application to the evaluation of fractional iterations of functions.
Superfunctions and their inverse functions (Abel functions) allow evaluation of not only minus-first power of a function (inverse function), but also any real and even complex iteration of the function.
Historically, the first function of such kind, iteration half of the exponential, id est, \(\sqrt{\exp}~\), is considered in 1950 by Hellmuth Kneser [2]. That time, no algorithm had been suggested for evaluation of this function.
Since 1960, function \(\sqrt{!~}~\) is accepted as logo of the Physics department of the Moscow State University, see the first picture of the figure at left.
Until year 2007, this symbol is believed to have no mathematical sense
[3][4][5].
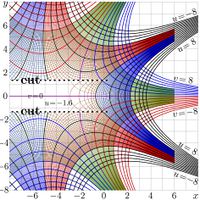
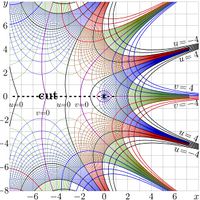
The complex maps of functions \( \sqrt{\exp} \) and \(\sqrt{!} \) are shown in figures at right.
Mathematicians of the same University were not so arrogant and used the symbol of integral and the Moebius surface at their logo, see second picture of the figure at left.
That time, researchers did not have computational facilities for evaluation of such functions, but the \(\sqrt{\exp}\) was more lucky than the \(~\sqrt{!~}~~\); at least the existence of holomorphic function \(\varphi\) such that \(\varphi(\varphi(z))=\exp(z)\) has been declared [2]. Actually, for his proof, Kneser had constructed the superfunction of exp and corresponding Abel function \(\mathcal{X}\), satisfying the Abel equation \[\mathcal{X}(\exp(z))=\mathcal{X}(z)+1\] . The inverse function, id est \(F=\mathcal \chi^{-1}\) is an entire super-exponential, although it is not real at the real axis; it cannot be interpreted as tetration, because the condition \(F(0)=1\) cannot be realized for the entire super-exponential. The real \(\sqrt{\exp}\) can be constructed with the tetration (which is also a superexponential), and the real \(\sqrt{\rm Factorial}\) can be constructed with the SuperFactorial. The plots of \(\sqrt{\rm Factorial}~\) and \(\sqrt{\exp}~\) in the compex plane are shown in the right hand side figure.
Extensions
The recurrent formula of the preamble can be written as equations
\(F(z\!+\!1)=T(F(z)) ~ \forall z\in \mathbb{N} : z>0\)
\(F(1)=t\)
Instead of the last equation, one could write
\(F(0)=t\)
and extend the range of definition of superfunction \(F\) to the non-negative integers. Then, one may postulate
\(F(-1)=T^{-1}(t)\)
and extend the range of validity to the negative integer values, at least while the inverse of the Transfer function is holomorphic. For example,
\(F(-2)=T^{-2}(t)=T^{-1}\Big(T^{-1}(t)\Big)\)
and so on. However, the inverse function may happen to be not defined for some values of \(t\).
The tetration is considered as super-function of exponential for some real base \(b\); in this case,
\(T=\exp_{b}\)
then, at \(t=1\),
\(F(-1)=\log_b(1)=0 ~ ~, ~ ~ \mathrm{but}\)
\(F(-2)=\log_b(0)~ \mathrm{~is~ not~ defined}\)
For extension to non-integer values of the argument, superfunction should be defined in different way.
Definition
For complex numbers \(~p~\) and \(~q~\), such that \(~p~\) belongs to some connected domain \(D\subseteq \mathbb{C}\),
superfunction (from \(p \mapsto q\)) of holomorphic function \(~T~\) on domain \(C \in \mathbb C\) is
function \( F \), holomorphic on domain \(D\), such that
\(F(z\!+\!1)=T(F(z)) ~ \forall z\in D : z\!+\!1 \in D\)
\(F(p)=q\)
Uniqueness
In general, the super-function is not unique. For a given base function \(T\), from given \((p\mapsto q)\) superfunction \(F\), another \((p \mapsto q)\) superfunction \(\tilde F\) could be constructed as \[\tilde F(z)=F(z+\mu(z))\] where \(\mu\) is any 1-periodic function, holomorphic at least in some vicinity of the real axis, such that \( \mu(p)=0 \).
The modified superfunction may have narrowed range of holomorphism. The narrower is the range of holomorphism, the wider is variety of superfunctions allowed [6].
At large enough range of holomorphism, the super-function is expected to be unique, for each specific specific transfer function \(T\). In particular, the \((C, 0\mapsto 1)\) super-function of \(\exp_b\), for \(b>1\), is called tetration and is believed to be unique at least for \(C= \{ z \in \mathbb{C} ~:~\Re(z)>-2 \}\); for the case \( b>\exp(1/\mathrm{e})\), see [7].
Examples
The short version of the table of superfunctions is suggested in [8]. A little bit more extended table is avilable at TORI [9]. Some superfunctions can be expressed with elementary functions, they are used without to mention that they are superfunctions. For example, for the transfer function "++", which means unity increment, the superfunction is just addition of a constant.
Addition
Chose a complex number \(c\) and define function \(\mathrm{add}_c\) with relation \(\mathrm{add}_c(z)=c\!+\!z ~ \forall z \in \mathbb{C}\) . Define function \(\mathrm{mul_c}\) with relation \(\mathrm{mul_c}(z)=c\!\cdot\! z ~ \forall z \in \mathbb{C}\).
Then, function \(~\mathrm{mul_c}~\) is superfunction (\(~0\) to \(~ c~\)) of function \(~\mathrm{add_c}~\) on \(~\mathbb{C}~\).
Multiplication
Exponentiation \(\exp_c\) is superfunction (from 1 to \(c\)) of function \(\mathrm{mul}_c \).
Quadratic polynomials
Let the transfer function \(T\) be defined with \(T(z)=2 z^2-1\). Then, \(F(z)=\cos( \pi \cdot 2^z) \) is a \((\mathbb{C},~ 0\! \rightarrow\! 1)\) superfunction of \(T\).
Indeed,
\(F(z\!+\!1)=\cos(2 \pi \cdot 2^z)=2\cos(\pi \cdot 2^z)^2 -1 =T(F(z))\)
and
\(F(0)=\cos(2\pi)=1\)
In this case, the superfunction \(F\) is periodic; its period
\(\tau=\frac{2\pi}{\ln(2)} \mathrm{i}\approx 9.0647202836543876194 \!~i \)
and the superfunction approaches unity also in the negative direction of the real axis,
\(\lim_{x\rightarrow -\infty} F(x)=1\)
The example above and the two examples below are suggested at [10]
In general, the transfer function \(T\) has no need to be entire function. Here is the example with meromorphic function \(T\). Let
\(T(z)=\frac{2z}{1-z^2} ~ \forall z\in D~\); \(~ D=\mathbb{C} \backslash \{-1,1\}\)
Then, function
\(F(z)=\tan(\pi 2^z)\)
is \((C, 0\! \mapsto\! 0)\) superfunction of function \(T\), where \(C\) is the set of complex numbers except singularities of function \(F\). For the proof, the trigonometric formula \(\displaystyle \tan(2 \alpha)=\frac{2 \tan(\alpha)}{1-\tan(\alpha)^2}~~ \forall \alpha \in \mathbb{C} \backslash \{\alpha\in \mathbb{C} : \cos(\alpha)=0 || \sin(\alpha)=\pm \cos(\alpha) \} \) can be used at \(\alpha=\pi 2^z \), that gives
\(\displaystyle T(F(z))=\frac{2 \tan(\pi 2^z)}{1-\tan(\pi 2^z)} = \tan(2 \pi 2^z)=F(z+1)\)
Algebraic function
In the similar way one can consider the transfer function
\(T(z)=2z \sqrt{1-z^2}\)
and
\(F(z)=\sin(\pi 2^z)\)
which is \((C,~ 0\!\rightarrow \!0)\) superfunction of \(H\) for \(C= \{z\in \mathbb C : \Re( \cos(\pi 2^z))>0 \}\).
Exponentiation
Let \(b>1\), \(T(z)= \exp_b(z)\), \( C= \{ z \in \mathbb{C} : \Re(z)>-2 \}\). Then, tetration \( \mathrm{tet}_b \) is a \((C,~ 0\! \rightarrow\! 1)\) superfunction of \(\exp_b\).
Abel function
Inverse of superfunction \(G=F^{-1}\) is called the Abel function; within some domain, it satisfies the Abel equation
\(T(G(z))=G(z)+1\)
Applications of superfunctions and the Abel functions
Superfunctions, usially the superexponentials, are proposed as a fast-growing function for an upgrade of the floating point representation of numbers in computers. Such an upgrade would greatly extend the range of huge numbers which are still distinguishable from infinity.
Other applications refer to the calculation of fractional iterates (or fractional power) of a function. Any holomorphic function can be declared as a "transfer function", then its superfunctions and corresponding Abel functions can be considered.
Nest
The \(c\)th iteration of some function \(f\) can be expressed through the superfunction \(F\) and the Abel function \(G=F^{-1}\):
- \( T^c(z)=F(c+G(z))\)
In Mathematica, there already exist the special name for the operation, that could evaluate such a expression. It is called Nest. [11]. This function has 3 arguments. The first argument indicates the name of the function. The second argument indicates the initial value. The third (and last) argument indicates the number of iterations. Then, the iteration of function \(T\) can be written as follows:
- \( T^c(z)=\mathrm {Nest}[T,z,c]\)
Unfortunately, in the version "Mathematica 8", the implementation of the Nest has serious restrictions: the number of iterations should allow the simplification to an integer constant. The intents to call function Nest with any other expression as the last argument cause the error messages. One may hope, in the future versions of Mathematica this bug will be corrected.
The table of known superfunctions and the corresponding Abel functions (similar to that suggested in [8]) could be loaded in Mathematica in a manned similar to that the table of integrals is loaded. This would allow the correct implementation of Nest for the case of non–integer number of iterations.
Transition from a function to its inverse function
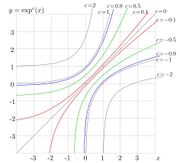
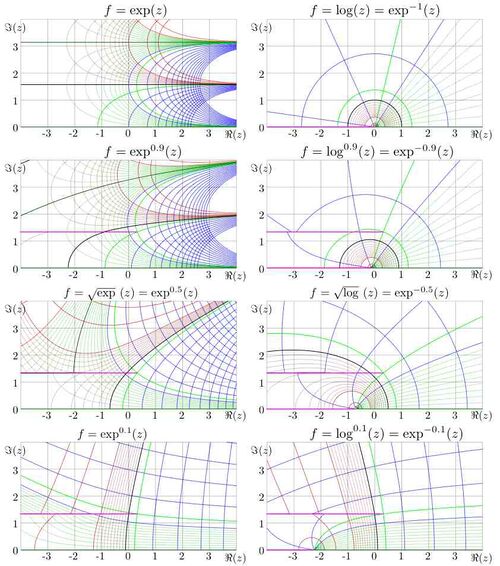
A superfunction \(S\) allows to calculate the fractional iteration \(H^c\) of some transfer function \(H\). Once the superfunction \(S\) and the Abel function \(A=S^{-1}\) are established, the fractional iteration can be defined as \(H^c(z)=S(c+A(z))\). Then, as \(c\) changes from 1 to \(-1\), the holomorphic transition from function \(H\) to \(H^{-1}\) is relalised. The figure at left shows an example of transition from \(\exp^{1}\!=\!\exp \) to \(\exp^{\!-1}\!=\!\ln \). Function \(\exp^c\) versus real argument is plotted for \(c=2,1,0.9, 0.5, 0.1, -0.1,-0.5, -0.9, -1,-2\). The tetrational and ArcTetrational were used as superfunction \(F\) and Abel function \(G\) of the exponential. The figure at right shows these functions in the complex plane. At non-negative integer number of iteration, the iterated exponential is entire function; at non-integer values, it has two branch points, thich correspond to the fixed points \(L\) and \(L^*\) of natural logarithm. At \(c\!\ge\! 0\), function \(\exp^c(z)\) remains holomorphic at least in the strip \(|\Im(z)|<\Im(L)\approx 1.3 \) along the real axis.
Nonlinear Optics
In the investigation of the nonlinear response of optical materials, the sample is supposed to be optically thin, in such a way, that the intensity of the light does not change much as it goes through. Then one can consider, for example, the absorption as function of the intensity. However, at small variation of the intensity in the sample, the precision of measurement of the absorption as function of intensity is not good. The reconstruction of the superfunction from the Transfer Function allows to work with relatively thick samples, improving the precision of measurements. In particular, the Transfer Function of the similar sample, which is half thiner, could be interpreted as the square root (id est, half-iteration) of the Transfer Function of the initial sample.
Similar example is suggested for a nonlinear optical fiber [7]. In particular, the Tania function can be evaluated using the Doya function and the regular iteration [12] at the fixed point \(0\), as \(\mathrm{Doya}_t(0)\!=\!0\). The same method can be applied also to other transfer functions, even if they cannot be easy represented through the special functions. This may refer, for example, to the experimentally–measured transfer function, that has no need to coincide with the Doya function.
Nonlinear Acoustics
It may have sense to characterize the nonlinearities in the attenuation of shock waves in a homogeneous tube. This could find an application in some advanced muffler, using nonlinear acoustic effects to withdraw the energy of the sound waves without to disturb the flux of the gas. Again, the analysis of the nonlinear response, id est, the Transfer Function, may be boosted with the superfunction.
Vaporization and condensation
In analysis of condensation, the growth (or vaporization) of a small drop of liquid can be considered, as it diffuses down through a tube with some uniform concentration of vapor. In the first approximation, at fixed concentration of the vapor, the mass of the drop at the output end can be interpreted as the Transfer Function of the input mass. The square root of this Transfer Function will characterize the tube of half length.
Snow avalanche
The mass of a snowball, that rolls down from the hill, can be considered as a function of the path it already have passed. At fixed length of this path (that can be determined by the altitude of the hill) this mass can be considered also as a Transfer Function of the input mass. The mass of the snowball could be measured at the top of the hill and at thе bottom, giving the Transfer Function; then, the mass of the snowball as a function of the length it passed is superfunction.
Operational element
If one needs to build-up an operational element with some given transfer function \(H\), and wants to realize it as a sequential connection of a couple of identical operational elements, then, each of these two elements should have transfer function \( h=\sqrt{T}\). Such a function can be evaluated through the superfunction and the Abel function of the transfer function \(T\).
The operational element may have any origin: it can be realized as an electronic microchip, or a mechanical couple of curvilinear grains), or some asymmetric U-tube filled with different liquids, and so on.
Other meanings of words
In mathematics, terms often have meaning, slightly deviating from terminology, used by the normal people.
Not all supperfunctions are holomorphic. Nest may be difficult to implement in Mathematica. Even term Superpower may have different meaning.
References
- ↑ https://opc.mfo.de/detail?photo_id=7607 On the Photo: Kneser, Hellmuth Location: Oberwolfach Author: Danzer, Ludwig (photos provided by Danzer, Ludwig) Source: L. Danzer, Dortmund Year: 1958 Copyright: L. Danzer, Dortmund Photo ID: 7607
- ↑ 2.0 2.1 http://mizugadro.mydns.jp/PAPERS/Relle.pdf Helmuth Kneser Reelle analytische L¨osungen der Gleichung \(\varphi(\varphi(x)) = e^x \) und verwandter Funktionalgleichungen Journal fur die reine und angewandte Mathematik 187 (1950) 56-67
- ↑ V.P.Kandidov. About the time and myself. (In Russian) 2007.05.18. http://ofvp.phys.msu.ru/pdf/Kandidov_70.pdf: .. По итогам студенческого голосования победителями оказались значок с изображением рычага, поднимающего Землю, и нынешний с хорошо известной эмблемой в виде корня из факториала, вписанными в букву Ф. Этот значок, созданный студентом кафедры биофизики А.Сарвазяном, привлекал своей простотой и выразительностью. Тогда эмблема этого значка подверглась жесткой критике со стороны руководства факультета, поскольку она не имеет физического смысла, математически абсурдна и идеологически бессодержательна. ..
- ↑ https://www.nkj.ru/archive/articles/1023/ V.Sadovnichi. 250 anniversary of the Moscow State University. (In Russian) В. Садовничий. ПЕРВОМУ УНИВЕРСИТЕТУ СТРАНЫ - 250! НАУКА И ЖИЗНЬ, №1, 2005. .. На значке физфака в букву "Ф" вписано стилизованное изображение корня из факториала (√!) - выражение, математического смысла не имеющее. ..
- ↑ Logo of the Physics Department of the Moscow State University. (In Russian); http://zhurnal.lib.ru/img/g/garik/dubinushka/index.shtml
- ↑ http://www.jstor.org/stable/2938713 P.Walker Infinitely differentiable generalized logarithmic and exponential functions Mathematics of computation, 196 (1991), 723-733
- ↑ 7.0 7.1 http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html (preprint: http://www.ils.uec.ac.jp/~dima/PAPERS/analuxp99.pdf ) D.Kouznetsov. Solutions of \(F(z+1)=\exp(F(z))\) in the complex \(z\)plane. Mathematics of Computation, 78 (2009) 1647-1670
- ↑ 8.0 8.1 http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12.
- ↑ http://tori.ils.uec.ac.jp/TORI/index.php/Table_of_superfunctions
- ↑ Mueller. Problems in Mathematics. http://www.math.tu-berlin.de/~mueller/projects.html
- ↑ http://reference.wolfram.com/mathematica/ref/Nest.html
- ↑ http://link.springer.com/article/10.1007/s10043-013-0058-6 Dmitrii Kouznetsov. Superfunctions for amplifiers. Optical Review, July 2013, Volume 20, Issue 4, pp 321-326. Preprint: http://mizugadro.mydns.jp/PAPERS/2013orSuper.pdf
- ↑ https://endless-sport.co.jp/products/suspension/index_superfunction.html Functionメーカー別適合表 ホーム> サスペンショントップ Super Function / スーパーファンクション(サーキット向け)(2020).
- ↑ https://www.pythonforbeginners.com/super/working-python-super-function Working with the Python Super Function. Last Updated: May 20, 2020. Python 2.2 saw the introduction of a built-in function called “super,” which returns a proxy object to delegate method calls to a class – which can be either parent or sibling in nature.
2014. https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 Dmitrii Kouznetsov. Суперфункции. Lambert Academic Publishing, 2014. (In Russian)
2016. https://doi.org/10.11568/kjm.2016.24.1.81 W.Paulsen, “FINDING THE NATURAL SOLUTION TO f(f(x)) = exp(x),” Korean Journal of Mathematics, vol. 24, no. 1, pp. 81–106, Mar. 2016.
2017. https://search.proquest.com/openview/cb7af40083915e275005ffca4bfd4685/1 S.Cowgill. Exploring Tetration in the Complex Plane. Arkansas State University, ProQuest Dissertations Publishing, 2017. 10263680.
2017. https://doi.org/10.1007/s10444-017-9524-1 W.Paulsen, S.Cowgill, Solving F(z + 1) = b ^ F(z) in the complex plane. Adv Comput Math 43, 1261–1282 (2017).
2018. https://doi.org/10.1080/10236198.2017.1307350 M.H. Hooshmand. (2018) Ultra power of higher orders and ultra exponential functional sequences. Journal of Difference Equations and Applications. Volume 24, 2018 - Issue 5: Special Issue: European Conference on Iteration Theory 2016. Special Issue Editors: Marek Cezary Zdun & Jaroslav Smital.
2019. https://doi.org/10.1007/s10444-018-9615-7 W.Paulsen. Tetration for complex bases. Adv Comput Math 45, 243–267 (2019).
2020. https://www.morebooks.de/store/gb/book/superfunctions/isbn/978-620-2-67286-3 D.Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.
2021. https://arxiv.org/abs/2101.03021v2 James David Nixon. Hyper-operations By Unconventional Means. March 8, 2021
Keywords
Abel function, Iteration, Regular iteration, SuperFactorial, Superfunctions, Transfer function, Transfer equation, Tetration, Tania function, Tania function, Shoka function, SuZex, SuTra