Difference between revisions of "Nemtsov function"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
(mainly formatting) |
||
| Line 1: | Line 1: | ||
| + | {{top}} |
||
| − | [[File:Nemplot.jpg|100px|thumb|Fig.1. \(y=\mathrm{Nem}_q(x)\) versus \(x\) for various \(q\)]] |
||
| + | <div class="thumb tright" style="float:right; margin:-76px 0px 4px 8px; line-height:2px; background-color:#fff"> |
||
| − | [[File:Nem100map.jpg|140px|thumb|Fig.2. \(u\!+\!\mathrm i v=\mathrm{Nem}_0(x\!+\!\mathrm i y)\)]] |
||
| − | + | {{pic|Nemplot.jpg|144px}}<small><center>Fig.1. \(y=\mathrm{Nem}_q(x)\)<!--<br> for various \(q\)!--></center></small> |
|
| + | </div> |
||
| − | [[File:Nembraplot.jpg|100px|thumb|Fig.4. \(x\!+\!\mathrm i y= \mathrm{NemBra}(q)\)]] |
||
| + | |||
| − | [[File:Nembrant.jpg|100px|thumb|Fig.5. \(x\!+\!\mathrm i y= \mathrm{NemBran}(q)\)]] |
||
| + | <div class="thumb tright" style="float:right; margin:4px 4px 6px 8px"> |
||
| − | [[File:Arqnem100map.jpg|160px|thumb|Fig.6. \(u\!+\!\mathrm i v=\mathrm{ArqNem}_0(x\!+\!\mathrm i y)\)]] |
||
| − | + | {{pic|Nem00map.jpg|200px}}<small><center>Fig.2. \(u\!+\!\mathrm i v=\mathrm{Nem}_0(x\!+\!\mathrm i y)\)</center></small><br> |
|
| + | <br> |
||
| + | |||
| + | {{pic|Nem120map.jpg|200px}}<small><center>Fig.3. \(u\!+\!\mathrm i v=\mathrm{Nem}_2(x\!+\!\mathrm i y)\)</center></small> |
||
| + | </div> |
||
| + | |||
| + | <div class="thumb tright" style="float:right; margin:6px 4px 12px 8px"> |
||
| + | {{pic|Arqnem100map.jpg|200px}}<small><center>Fig.6. \(u\!+\!\mathrm i v=\mathrm{ArqNem}_0(x\!+\!\mathrm i y)\)</center></small> |
||
| + | <br> |
||
| + | |||
| + | {{pic|Arqnem120map.jpg|200px}}<small><center>Fig.7. \(u\!+\!\mathrm i v=\mathrm{ArqNem}_2(x\!+\!\mathrm i y)\)</center></small> |
||
| + | </div> |
||
[[Nemtsov function]] is polynomial of special kind, suggested as an example of a [[transfer function]] |
[[Nemtsov function]] is polynomial of special kind, suggested as an example of a [[transfer function]] |
||
| − | for |
+ | for book «[[Superfunctions]]» <ref name="book"> |
| + | https://www.amazon.co.jp/-/en/Dmitrii-Kouznetsov/dp/6202672862 <br> |
||
| + | https://www.morebooks.de/shop-ui/shop/product/978-620-2-67286-3 <br> |
||
| + | https://mizugadro.mydns.jp/BOOK/468.pdf <br> |
||
| + | Dmitrii Kouznetsov. [[Superfunctions]]. [[Lambert Academic Publishing]], 2020. |
||
| + | </ref>, 2020.<br> |
||
| + | The description is loaded also as the [[Mizugadro Preprint]] <ref> |
||
| + | https://mizugadro.mydns.jp/PAPERS/2016nemtsov.pdf |
||
| + | Dmitrii Kouznetsov. |
||
| + | Nemtsov function and its iterates. |
||
| + | [[Mizugadro Preprint]], 2016. |
||
| + | </ref>. |
||
The [[Nemtsov function]] \(y=\mathrm{Nem}_q(x)= x+x^3+q x^4\) |
The [[Nemtsov function]] \(y=\mathrm{Nem}_q(x)= x+x^3+q x^4\) |
||
| Line 15: | Line 37: | ||
[[Complex map]] of \(\mathrm{Nem}_q\) is shown in figure 2 for \(q\!=\!0\) and in figure 3 for \(q\!=\!2\) with lines \(u\!=\!\mathrm{const}\) and |
[[Complex map]] of \(\mathrm{Nem}_q\) is shown in figure 2 for \(q\!=\!0\) and in figure 3 for \(q\!=\!2\) with lines \(u\!=\!\mathrm{const}\) and |
||
lines \(v\!=\!\mathrm{const}\) assuming that \(u\!+\!\mathrm i v=\mathrm{Nem}_0(x\!+\!\mathrm i y)\) . |
lines \(v\!=\!\mathrm{const}\) assuming that \(u\!+\!\mathrm i v=\mathrm{Nem}_0(x\!+\!\mathrm i y)\) . |
||
| + | |||
| + | ==Motivation== |
||
| + | |||
| + | The [[Nemtsov function]] appears as a simple example real-holomorphic transfer function with real [[fixed point]] such that the [[regular iteration]] method cannot be applies «as is».<br> |
||
| + | Editor did not found any example of such a kind simpler than the polynomial. |
||
| + | |||
| + | The [[Nemtsov function]] is considered as an attempt to suggest an «exotic» [[transfer function]] for which the |
||
| + | [[superfunction]] cannot be constructed as an analogy of other [[superfunctions]] |
||
| + | already built up for other transfer functions, see «[[Table of superfunctions]]». |
||
| + | |||
| + | The attempt failed; the [[Superfunction]] for the [[Nemtsov function]] is constructed and described below. |
||
| + | |||
| + | The need of the special name for this function had been revealed 2015.02.27, in the day, when [[Putin killed Nemtsov]]. <br> |
||
| + | To year 2025, no other [[scientific concept]] of that murder had been suggested. <br> |
||
| + | Apparently, the total [[corruption]] in Russia <ref name="medvedko"> |
||
| + | http://kremlin.ru/transcripts/1566 Д.Медведев. Вступительное слово на заседании Совета по противодействию коррупции. 30 сентября 2008 года, 16:25 Москва, Кремль. Д.Медведев: Коррупция в нашей стране приобрела не просто масштабный характер, она стала привычным, обыденным явлением, которое характеризует саму жизнь в нашем обществе... |
||
| + | </ref> does not allow the professionals to investigate that case, and that terroristic act caused many publications. This makes the family name "Nemtsov" to be a good mark, label on the timeline of Human History. |
||
| + | |||
| + | To year 2025, no better notation for this special polynomial is found in publications.<br> |
||
| + | For this reason, the notation «[[Nemtsov function]]» is used at site [[Mizugadro]]. |
||
==Definition== |
==Definition== |
||
| − | Let \(q\) be |
+ | Let \(q\) be non-negative real parameter. Then, [[Nemtsov function]] \(\mathrm{Nem}\) is defined for complex argument \(z\) as follows: |
(1)\(~ ~ ~ ~ ~ ~ \mathrm{Nem}_q(z)= z+z^3+q z^4\) |
(1)\(~ ~ ~ ~ ~ ~ \mathrm{Nem}_q(z)= z+z^3+q z^4\) |
||
| Line 24: | Line 66: | ||
==Notations== |
==Notations== |
||
| − | For Function \(~ \mathrm{Nem}_q~\) by equation (1), at \(q\!>\!0\), the algorithms, described in the first edition of the Russian version of the book [[Суперфункции]] cannot be applied "as is", and some modification, |
+ | For Function \(~ \mathrm{Nem}_q~\) by equation (1), at \(q\!>\!0\), the algorithms, described in the first edition of the Russian version of the book «[[Суперфункции]]» (2014) cannot be applied "as is", and some modification, generalization is required. |
| − | For this reason, function \(\mathrm{Nem}_q\) by equation (1) is |
+ | For this reason, function \(\mathrm{Nem}_q\) by equation (1) is considered. |
| − | In this article, properties of the Nemtsov function are considered, and also some properties of the related functions: |
+ | In this article, properties of the [[Nemtsov function]] are considered, and also some properties of the related functions: |
Inverse function, denoted with [[ArqNem]], |
Inverse function, denoted with [[ArqNem]], |
||
| Line 54: | Line 96: | ||
added to the notation, in order to distinguish this iterate from other iterates, constructed, for example, using the asymptotic behaviour of the [[Nemtsov function]] (and its iterates) at infinity. |
added to the notation, in order to distinguish this iterate from other iterates, constructed, for example, using the asymptotic behaviour of the [[Nemtsov function]] (and its iterates) at infinity. |
||
| + | ==[[NemBran]] and [[NemBra]]== |
||
| − | ==General properties== |
||
| + | <div class="thumb tright" style="float:right; margin:-40px 2px 200px 2px; width:410px; height:460px;"> |
||
| + | <p style="margin:0px 0px 0px 9px;line-height:0px; width:200px; background-color:#fff"> {{pic|Nembraplot.jpg|180px}}</p> |
||
| + | <p style="margin:-440px 0px 440px 220px;line-height:0px">{{pic|Nembrant.jpg|180px}}</p> |
||
| + | <p style="margin:-432px 0px 4px 12px;"> Fig.4: \(x\!+\!\mathrm i y= \mathrm{NemBran}(q) ~\) and \(~ x\!+\!\mathrm i y= \mathrm{NemBra}(q)\)</p> |
||
| + | </div> |
||
| + | <!-- |
||
| + | <div class="thumb tright" style="float:right; margin:2px 0px 2px 8px"> |
||
| + | {{pic|Nembrant.jpg|144px}}<small><center>Fig.5. \(x\!+\!\mathrm i y= \mathrm{NemBran}(q)\)</center></small> |
||
| + | </div> |
||
| + | !--> |
||
For real \(q\), the [[Nemtsov function]] is real holomorphic in the whole complex plane; |
For real \(q\), the [[Nemtsov function]] is real holomorphic in the whole complex plane; |
||
\(\mathrm{Nem}_q(z^*)=\mathrm{Nem}_q(z)^*\) |
\(\mathrm{Nem}_q(z^*)=\mathrm{Nem}_q(z)^*\) |
||
| − | At least for positive values of the argument, the Nemtsov function grows monotonously. |
+ | At least for positive values of the argument, the Nemtsov function grows monotonously.<br> |
| − | The monotonous growth |
+ | The monotonous growth is also property of the inverse function [[ArqNem]], that of the [[Abelfunction]] [[AuNem]] and that of the real iterates of the [[Nemtsov function]]. |
| − | + | For any non-trivial entire function, the inverse function \(\mathrm{ArqNem}_q\) has the branch points. <br> |
|
| + | Two of them are complex; and one of them is expressed with function [[NemBran]].<br> |
||
| − | at \(z=\mathrm{NemBran}(q)\), function \(\mathrm{ArqNem}_q(z)\) has infinite derivative. |
||
| + | Parametric plot of function [[NemBran]] is shown at first picture in figure 4.<br> |
||
| + | At \(z=\mathrm{NemBran}(q)\), function \(\mathrm{ArqNem}_q(z)\) has infinite derivative. |
||
| − | For construction of the inverse function, important are the complex soluitons \(A\) of equation \(\mathrm{Nem}_q^{\prime}=0\). |
+ | For construction of the inverse function, important are the complex soluitons \(A\) of equation \(\mathrm{Nem}_q^{\prime}=0\).<br> |
| − | One of these solutions is expressed with function [[NemBra]], id est, \(A=\mathrm{NemBra}(q)\). |
+ | One of these solutions is expressed with function [[NemBra]], id est, \(A=\mathrm{NemBra}(q)\). |
| + | Parametric plots of functions [[NemBra]] and [[NemBran]] are shown in figure 5; |
||
| − | \( |
+ | \(\mathrm{NemBran}(q)=\mathrm{Nem}_q\big(\mathrm{NemBra}(q)\big)\) : |
| + | \( |
||
| − | \(y=\mathrm{Im}\big(\mathrm{NemBra}(q)\big)~\) |
||
| + | \left( |
||
| + | \begin{array}{cc} |
||
| + | x=\mathrm{Re}\big(\mathrm{NemBran}(q)\big) \\ |
||
| + | y=\mathrm{Im}\big(\mathrm{NemBran}(q)\big) |
||
| + | \end{array}\right) |
||
| + | ~\), left and |
||
| + | \(~ |
||
| + | \left( |
||
| + | \begin{array}{cc} |
||
| + | x=\mathrm{Re}\big(\mathrm{NemBra}(q)\big) \\ |
||
| + | y=\mathrm{Im}\big(\mathrm{NemBra}(q)\big) |
||
| + | \end{array}\right) |
||
| + | ~\) , right. |
||
For positive \(q\), both real and imaginary parts of the branchpoint are significantly smaller than unity. |
For positive \(q\), both real and imaginary parts of the branchpoint are significantly smaller than unity. |
||
| + | |||
| + | As function [[NemBra]] is implemented, the efficient algorithm for evaluation of the inverse functions of the [[Nemtsov function]] |
||
| + | can be constructed.<br> |
||
| + | Three of them are denoted with symbols «[[ArcNem]]», «[[ArkNem]]», «[[ArqNem]]». <br> |
||
| + | One of them ([[ArqNem]]) is described in the next section. |
||
==Inverse function== |
==Inverse function== |
||
| Line 81: | Line 154: | ||
\(\mathrm{Nem}_q(A)=z\) |
\(\mathrm{Nem}_q(A)=z\) |
||
| − | has many solutions \(A\) ; there are three solutions for \(q\!=\!0\) and four for \(q\!\ne\!0\). |
+ | has many solutions \(A\) ; there are three solutions for \(q\!=\!0\) and four for \(q\!\ne\!0\). <br> |
| + | The holomorphic inverse function unavoidably has the cut lines.<br> |
||
The appropriate choice of these cut lines happens to be non–trivial problem. |
The appropriate choice of these cut lines happens to be non–trivial problem. |
||
| − | For construction of the [[ |
+ | For construction of the [[Abelfunction]], denoted as [[AuNem]], the special inverse function [[ArqNem]] of the [[Nemtsov function]] is chosen. <br> |
| + | For function [[ArqNem]], the cut lines are chosen in the following way.<br> |
||
| − | One cut line goes along the negative part of the real axis from \(-\infty\) to zero. |
||
| + | One cut line goes along the negative part of the real axis from \(-\infty\) to zero.<br> |
||
| − | Two other cut lines go straightly from zero to the complex branchpoints \(Z_o\) of the inverse function. |
||
| + | Two other cut lines go straightly from zero to the complex branchpoints \(Z_{\mathrm o}\) of the inverse function.<br> |
||
These brach points can be expressed in the following way: |
These brach points can be expressed in the following way: |
||
| − | \(Z_{\mathrm o}=\mathrm{Nem}_q(z_{\mathrm |
+ | \(Z_{\mathrm o}=\mathrm{Nem}_q(z_{\mathrm{o}})\) |
where \(z_{\mathrm o}=\mathrm{NemBran}(q)\) is solution of equation |
where \(z_{\mathrm o}=\mathrm{NemBran}(q)\) is solution of equation |
||
| Line 111: | Line 186: | ||
\(u\!+\!\mathrm i v= \mathrm{ArqNem}_q(x\!+\!\mathrm i y)\) |
\(u\!+\!\mathrm i v= \mathrm{ArqNem}_q(x\!+\!\mathrm i y)\) |
||
| + | The complex double implementation of function [[ArqNem]] is loaded as [[arqnem.cin]].<br> |
||
| − | The complex double implementation of function [[ArqNem]] is loaded as [[arqnem.cin]] ; parameter \(q\) is storem in the global variable \(Q\). Before evaluation of \(\mathrm{ArqNem}_q\) of complex argument, the complex branch point should be evaluated with routine [[nembran.cin]] and stored in the global variables tr and ti; in the version from year 2015, the real and imaginary parts of the branch point are stored as two global variables. |
||
| + | In the implementation, parameter \(q\) is stored in the global variable \(Q\). Perhaps, it would not be a good solution for any software, |
||
| + | but this happen to be a simplest way to plot pictures for book «[[Superfunctions]]» <ref name="book"/>. |
||
| + | |||
| + | Before evaluation of \(\mathrm{ArqNem}_q\) of complex argument, the complex branch point should be evaluated with routine [[nembran.cin]] and stored in the global variables tr and ti; in the version from year 2015, the real and imaginary parts of the branch point are stored as two global variables. |
||
At any change of parameter \(q\), these values should be recalculated. |
At any change of parameter \(q\), these values should be recalculated. |
||
==Superfunction== |
==Superfunction== |
||
| + | <div class="thumb tleft" style="float:left; margin:-8px 8px 0px 0px; background-color:#fff"> |
||
| − | [[File:Sunemplo4t.jpg|180px|left|thumb|\(y\!=\!\mathrm{SuNem}_{q}(x)\) for various \(q\)]] |
||
| + | {{pic|Sunemplo4t.jpg|180px}}<small><center>\(y\!=\!\mathrm{SuNem}_{q}(x)\) for various \(q\)</center></small> |
||
| − | <!-- |
||
| + | </div> |
||
| − | [[File:Sunemplot.jpg|200px|left| thumb|\(y\!=\!\mathrm{SuNem}_q(x)\) for |
||
| + | |||
| − | \(q\!=\!0\), |
||
| + | <div class="thumb tright" style="float:right; margin:2px 0px 0px 8px"> |
||
| − | \(q\!=\!1\) and for |
||
| + | {{pic|Sunem0map6.jpg|200px}}<small><center>\(u\!+\!\mathrm i v=\mathrm{SuNem}_0(x\!+\!\mathrm i y)\)</center></small> |
||
| − | \(q\!=\!2\)]]!--> |
||
| + | |||
| − | [[File:Sunem0map6.jpg|200px|thumb|\(u\!+\!\mathrm i v=\mathrm{SuNem}_0(x\!+\!\mathrm i y)\)]] |
||
| − | + | {{pic|Sunem1map6.jpg|200px}}<small><center>\(u\!+\!\mathrm i v=\mathrm{SuNem}_1(x\!+\!\mathrm i y)\)</center></small> |
|
| + | |||
| − | [[File:Sunem2map6.jpg|200px|thumb|\(u\!+\!\mathrm i v=\mathrm{SuNem}_2(x\!+\!\mathrm i y)\)]] |
||
| + | {{pic|Sunem2map6.jpg|200px}}<small><center>\(u\!+\!\mathrm i v=\mathrm{SuNem}_2(x\!+\!\mathrm i y)\)</center></small> |
||
| + | </div> |
||
| + | |||
For the [[Nemtsov function]] |
For the [[Nemtsov function]] |
||
\(\mathrm{Nem}_q\), the [[superfunction]] \(\mathrm{SuNem}_q~\) is real–holomorphic solution \(F\) of the [[transfer equation]] |
\(\mathrm{Nem}_q\), the [[superfunction]] \(\mathrm{SuNem}_q~\) is real–holomorphic solution \(F\) of the [[transfer equation]] |
||
| Line 141: | Line 223: | ||
Explicit plot of function [[SuNem]] of the real argument is shown in figure at left, \(y\!=\!\mathrm{SuNem}_q(x)\) is plotted versus \(x\) for various values of \(q\). |
Explicit plot of function [[SuNem]] of the real argument is shown in figure at left, \(y\!=\!\mathrm{SuNem}_q(x)\) is plotted versus \(x\) for various values of \(q\). |
||
| + | |||
Function [[SuNem]] grows monotonously from zero at \(-\infty\), takes value unity at zero and then grows quickly to infinity for positive values of the argument. |
Function [[SuNem]] grows monotonously from zero at \(-\infty\), takes value unity at zero and then grows quickly to infinity for positive values of the argument. |
||
| + | |||
| − | The larger is parameter \(q\), the faster is the growth at \(+\infty\). This behaviour corresponds to the intuitive expectations about this function. |
||
| + | The larger is parameter \(q\), the faster is the growth at \(+\infty\). |
||
| + | |||
| + | This behaviour corresponds to the intuitive expectations about this function. |
||
Complex maps of function [[SuNem]] are shown in figures at right for \(q\!=\!0\), \(q\!=\!1\) and for \(q\!=\!2\); |
Complex maps of function [[SuNem]] are shown in figures at right for \(q\!=\!0\), \(q\!=\!1\) and for \(q\!=\!2\); |
||
| Line 148: | Line 234: | ||
\(u\!+\!\mathrm i v=\mathrm{SuNem}_q(x\!+\!\mathrm i y)\) |
\(u\!+\!\mathrm i v=\mathrm{SuNem}_q(x\!+\!\mathrm i y)\) |
||
| − | Maps for different values of \(q\) look similar; however, the greater is \(q\), the faster is the growth of \(\mathrm{SuNem}_q\) along the real axis. |
+ | Maps for different values of \(q\) look similar; however, the greater is \(q\), the faster is the growth of \(\mathrm{SuNem}_q\) along the real axis. <br> |
| + | This is seen also at the explicit plot in figure at left. |
||
| − | In order to construct function [[SuNem]], first, any superfunction \(F\) with appropriate asymptotic behaviour is constructed |
+ | In order to construct function [[SuNem]], first, any superfunction \(F\) with appropriate asymptotic behaviour is constructed. |
| + | <br> |
||
| + | Then, \(\mathrm{SuNem}_q(z)=F(x_1+z)\) where \(x_1\) is real solution of equation \(F(x_1)=1\). |
||
| + | ==[[Abelfunction]]== |
||
| − | ==Abel function== |
||
| + | <div style="float:left; width:200px; margin:-6px 18px 5px 0px; background-color:#fff; width:210px"> |
||
| − | [[File:Aunemplot.jpg|160px|left|thumb|\(y\!=\!\mathrm{AuNem}_q(x)\) for |
||
| + | {{pic|Aunemplot.jpg|200px}}<small><center>\(y\!=\!\mathrm{AuNem}_q(x)\) for \(q\!=\!0\), \(q\!=\!1\) and \(q\!=\!2\) </center></small> |
||
| − | \(q\!=\!0\), |
||
| + | </div> |
||
| − | \(q\!=\!1\) and |
||
| − | \(q\!=\!2\)]] |
||
For the [[Abel function]] of the [[Nemtsov function]], notation [[AuNem]] is suggested. |
For the [[Abel function]] of the [[Nemtsov function]], notation [[AuNem]] is suggested. |
||
| Line 163: | Line 251: | ||
\(q\!=\!1\) and |
\(q\!=\!1\) and |
||
\(q\!=\!2\). |
\(q\!=\!2\). |
||
| + | |||
| − | The same plot can be obtained, reflecting the curves for [[SuNem]] from the bisektris of the First quadrant of the coordinate plane. This property can be used as a mumerical test of relation \(\mathrm{SuNem}_q(\mathrm{АuNem}_q(x))=x\); it should be so, as |
||
| + | The same plot can be obtained, reflecting the curves for [[SuNem]] from the angle bisector of the First quadrant of the coordinate plane. |
||
| + | |||
| + | This property can be used as a mumerical test of relation |
||
| + | |||
| + | \(\mathrm{SuNem}_q(\mathrm{АuNem}_q(x))=x\); |
||
| + | |||
| + | it should be so, while |
||
\(\mathrm{AuNem}_q=\mathrm{SuNem}_q^{-1}\) |
\(\mathrm{AuNem}_q=\mathrm{SuNem}_q^{-1}\) |
||
| Line 178: | Line 273: | ||
The asymptotic expansion of function [[AuNem]] at zero can be found, inverting the asymptotic expansion of function [[SuNem]] at \(-\infty\); |
The asymptotic expansion of function [[AuNem]] at zero can be found, inverting the asymptotic expansion of function [[SuNem]] at \(-\infty\); |
||
| − | the coeffcieints of this expansion can be found also from the Abel equation. |
+ | the coeffcieints of this expansion can be found also from the Abel equation. |
| + | <br> |
||
| + | The expansion can be written as follows: |
||
==Iterates of the [[Nemtsov function]]== |
==Iterates of the [[Nemtsov function]]== |
||
| + | <div class="thumb tright" style="float:right; margin:0px 0px 2px 8px"> |
||
| − | [[File:Itnem00plot.jpg|200px|thumb|\(y\!=\!\mathrm{Nem}_0^{\,n}(x)\) versus \(x\) at various \(n\)]] |
||
| − | + | {{pic|Itnem00plot.jpg|200px}}<small><center>\(y\!=\!\mathrm{Nem}_0^{\,n}(x)\) versus \(x\) at various \(n\)</center></small> |
|
| − | + | {{pic|Itnem10plot.jpg|200px}}<small><center>\(y\!=\!\mathrm{Nem}_1^{\,n}(x)\) versus \(x\) at various \(n\)</center></small> |
|
| + | {{pic|Itnem20plot.jpg|200px}}<small><center>\(y\!=\!\mathrm{Nem}_2^{\,n}(x)\) versus \(x\) at various \(n\)</center></small> |
||
| + | </div> |
||
With functions [[SuNem]] and [[AuNem]], the \(n\)th [[iterate]] of the [[Nemtsov function]] can be expressed as follows |
With functions [[SuNem]] and [[AuNem]], the \(n\)th [[iterate]] of the [[Nemtsov function]] can be expressed as follows |
||
| Line 189: | Line 288: | ||
\(\mathrm{Nem}_q^{\,n}(z)=\mathrm{AuNem}_q\big( n+\mathrm{AuNem}_q(z)\big)\) |
\(\mathrm{Nem}_q^{\,n}(z)=\mathrm{AuNem}_q\big( n+\mathrm{AuNem}_q(z)\big)\) |
||
| − | For |
+ | For <br> |
| − | \(q\!=\!0\), |
+ | \(q\!=\!0\),<br> |
| − | \(q\!=\!1\) and for |
+ | \(q\!=\!1\) and for<br> |
| − | \(q\!=\!2\), |
+ | \(q\!=\!2\),<br> |
| − | these iterates are shown in figures at right. |
+ | these iterates are shown in figures at right.<br> |
These iterates look similar to other iterates of the fast growing functions. |
These iterates look similar to other iterates of the fast growing functions. |
||
| Line 199: | Line 298: | ||
at negative values of \(n\), the growth is slow. |
at negative values of \(n\), the growth is slow. |
||
| − | The zeroth iterate (\(n\!=\!0\)), the iterates apperas as identity function. |
+ | The zeroth iterate (\(n\!=\!0\)), the iterates apperas as identity function. <br> |
| + | In the figures, the corresponding graphics are marked with green lines. |
||
| − | Due to the singularity of function [[ArqNem]] at zero, the |
+ | Due to the singularity of function [[ArqNem]] at zero, the non-integer iterates are not defined at zero and the negative part of the real axis, although they approach zero as the positive argument of the iterate becomes small. |
The curves of the iterates show the symmetry with respect to reflections from the bisectris of the First quadrant of the coordinate plane, as |
The curves of the iterates show the symmetry with respect to reflections from the bisectris of the First quadrant of the coordinate plane, as |
||
| Line 207: | Line 307: | ||
\(\mathrm{Nem}_q^{-n}(z)=\mathrm{ArqNem}_q^{\,n}(z)\) |
\(\mathrm{Nem}_q^{-n}(z)=\mathrm{ArqNem}_q^{\,n}(z)\) |
||
| − | == |
+ | ==Application and the Discussion== |
The [[Nemtsov function]] is considered as a candidate of the [[transfer function]], for which the |
The [[Nemtsov function]] is considered as a candidate of the [[transfer function]], for which the |
||
[[superfunction]] and the [[Abel function]] are diffucult to construct with the [[exotic iterate]] at its [[fixed point]] zero. |
[[superfunction]] and the [[Abel function]] are diffucult to construct with the [[exotic iterate]] at its [[fixed point]] zero. |
||
| Line 215: | Line 315: | ||
For the [[Nemtsov function]], two other [[inverse function]]s have been constructed, they are denoted with hames |
For the [[Nemtsov function]], two other [[inverse function]]s have been constructed, they are denoted with hames |
||
| − | [[ArcNem]] and [[ArkNem]]. |
+ | [[ArcNem]] and [[ArkNem]]. |
| + | <br> |
||
| + | They have different positions of the cut lines, and, at the iterates, do not provide the |
||
holomorphic Abel function. |
holomorphic Abel function. |
||
| − | Once the iterates of the inverse function leads to the fixed point of the transfer function, the exotic iterates are straightforward. |
+ | Once the iterates of the inverse function leads to the fixed point of the transfer function, the exotic iterates are straightforward. |
| + | <br> |
||
| + | Other transfer functions can be considered in the similar way, assuming, that their expansion at the fixed point begins with the identity function and the cubic term. |
||
| + | <br> |
||
| + | Without loss of generality, the coefficient at the cubic term can be treated as unity; the corresponding transform to this case is shown in the last row of the |
||
[[Table of superfunctions]]. |
[[Table of superfunctions]]. |
||
| + | |||
| + | ==Warning== |
||
| + | |||
| + | The name «[[Nemtsov function]]» is chosen as a simplest mnemonic that refers to the history of century 21. |
||
| + | |||
| + | The naming is not an attempt to remind the Russian usurper and his crime accomplices that |
||
| + | it is not a good style, to kill the political opponent. |
||
| + | <br> |
||
| + | The growth of [[corruption]] <ref name="medvedko"> |
||
| + | http://kremlin.ru/transcripts/1566 Д.Медведев. Вступительное слово на заседании Совета по противодействию коррупции. 30 сентября 2008 года, 16:25 Москва, Кремль. Д.Медведев: Коррупция в нашей стране приобрела не просто масштабный характер, она стала привычным, обыденным явлением, которое характеризует саму жизнь в нашем обществе... |
||
| + | </ref> at putin's [[pahanat]] indicates that no any moral criteria nor moral concepts can be applied to Russia usurper and his accomplices. |
||
| + | So, the attempt mentioned would be just wane. |
||
| + | |||
| + | However, Editor keeps his right to call things in the most convenient and efficient system of notations. |
||
==References== |
==References== |
||
| + | {{ref}} |
||
| − | <references/> |
||
| + | 2016. |
||
http://mizugadro.mydns.jp/2016NEMTSOV/TRY00/23.pdf |
http://mizugadro.mydns.jp/2016NEMTSOV/TRY00/23.pdf |
||
| − | Dmitrii Kouznetsov. Nemtsov function and its iterates. 2016, |
+ | Dmitrii Kouznetsov. Nemtsov function and its iterates. 2016, [[Mizugadro Preprint]]. |
| + | {{fer}} |
||
| − | ==Keywords== |
||
| − | [[Abel function]], |
||
| − | [[ArqNem]], |
||
| − | [[AuNem]], |
||
| − | [[Book]], |
||
| − | [[C++]], |
||
| − | [[Exotic iterate]], |
||
| − | [[Latex]], |
||
| − | [[Mathematica]], |
||
| − | [[Nemtsov function]], |
||
| − | [[Putin killed Nemtsov]], |
||
| − | [[SuNem]], |
||
| − | [[Superfunction]], |
||
| − | [[Superfunctions]], |
||
| − | [[Table of superfunctions]] |
||
| + | ==Keywords== |
||
| + | «[[Abel function]]», |
||
| + | «[[ArqNem]]», |
||
| + | «[[AuNem]]», |
||
| + | «[[Book]]», |
||
| + | «[[C++]]», |
||
| + | «[[Exotic iterate]]», |
||
| + | «[[Exotic iteration]]», |
||
| + | «[[Latex]]», |
||
| + | «[[Mathematica]]», |
||
| + | «[[Nemtsov function]]», |
||
| + | «[[Putin killed Nemtsov]]», |
||
| + | «[[SuNem]]», |
||
| + | «[[Superfunction]]», |
||
| + | «[[Superfunctions]]», |
||
| + | «[[Table of superfunctions]]», |
||
[[Category:Abel function]] |
[[Category:Abel function]] |
||
| + | [[Category:Abelfunction]] |
||
[[Category:ArqNem]] |
[[Category:ArqNem]] |
||
[[Category:AuNem]] |
[[Category:AuNem]] |
||
Revision as of 15:51, 17 October 2025




Nemtsov function is polynomial of special kind, suggested as an example of a transfer function
for book «Superfunctions» [1], 2020.
The description is loaded also as the Mizugadro Preprint [2].
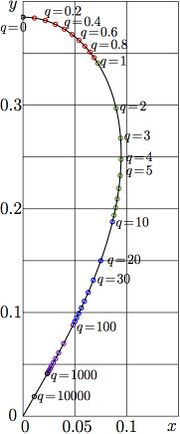
The Nemtsov function \(y=\mathrm{Nem}_q(x)= x+x^3+q x^4\) is shown in figure at right versis \(x\) for various \(q\!\ge\!0\).
Complex map of \(\mathrm{Nem}_q\) is shown in figure 2 for \(q\!=\!0\) and in figure 3 for \(q\!=\!2\) with lines \(u\!=\!\mathrm{const}\) and lines \(v\!=\!\mathrm{const}\) assuming that \(u\!+\!\mathrm i v=\mathrm{Nem}_0(x\!+\!\mathrm i y)\) .
Motivation
The Nemtsov function appears as a simple example real-holomorphic transfer function with real fixed point such that the regular iteration method cannot be applies «as is».
Editor did not found any example of such a kind simpler than the polynomial.
The Nemtsov function is considered as an attempt to suggest an «exotic» transfer function for which the superfunction cannot be constructed as an analogy of other superfunctions already built up for other transfer functions, see «Table of superfunctions».
The attempt failed; the Superfunction for the Nemtsov function is constructed and described below.
The need of the special name for this function had been revealed 2015.02.27, in the day, when Putin killed Nemtsov.
To year 2025, no other scientific concept of that murder had been suggested.
Apparently, the total corruption in Russia [3] does not allow the professionals to investigate that case, and that terroristic act caused many publications. This makes the family name "Nemtsov" to be a good mark, label on the timeline of Human History.
To year 2025, no better notation for this special polynomial is found in publications.
For this reason, the notation «Nemtsov function» is used at site Mizugadro.
Definition
Let \(q\) be non-negative real parameter. Then, Nemtsov function \(\mathrm{Nem}\) is defined for complex argument \(z\) as follows:
(1)\(~ ~ ~ ~ ~ ~ \mathrm{Nem}_q(z)= z+z^3+q z^4\)
Notations
For Function \(~ \mathrm{Nem}_q~\) by equation (1), at \(q\!>\!0\), the algorithms, described in the first edition of the Russian version of the book «Суперфункции» (2014) cannot be applied "as is", and some modification, generalization is required.
For this reason, function \(\mathrm{Nem}_q\) by equation (1) is considered.
In this article, properties of the Nemtsov function are considered, and also some properties of the related functions:
Inverse function, denoted with ArqNem,
\(\mathrm{Nem}_q(\mathrm{ArqNem}_q(z))=z\)
Superfunction, denoted with SuNem,
\(\mathrm{SuNem}_q(z\!+\!1)=\mathrm{Nem}_q(\mathrm{SuNem}_q(z))\)
Abel function, denoted with SuNem,
\(\mathrm{SuNem}_q(\mathrm{Nem}_q(z))=\mathrm{SuNem}_q(z)+1\)
and the corresponding iterates
\(\mathrm{Nem}_q^n(z)=\mathrm{SuNem}_q\big(n+ \mathrm{SuNem}_q(z)\big)\)
The inverse function is called ArqNem. This name allows to distinguish it from other inverse functions of the Nemtsov function. Two other inverse functions are called ArcNem and ArkNem. A priori, it had been difficult to guess, that namely ArqNem happens to be suitable for construction of the corresponding Abel function; so, all the three versions had been assigned (designated) the different names. These inverse functions have different positions of the cuts of the range of holomorphism.
The Abel function for the Nemtov function is called AuNem, to indicate, that it is constructed by the exotic iterates at the fixed point zero, that is maximal (Upper) among the fixed points of the Nemtsov function.
While no other iterates of the Nemtsov function are presented no special mark is used to denote the iterates \(\mathrm{Nem}_q^n\). Later, perhaps, one additional subscript \(_{\mathrm u}\) will be added to the notation, in order to distinguish this iterate from other iterates, constructed, for example, using the asymptotic behaviour of the Nemtsov function (and its iterates) at infinity.
NemBran and NemBra
For real \(q\), the Nemtsov function is real holomorphic in the whole complex plane;
\(\mathrm{Nem}_q(z^*)=\mathrm{Nem}_q(z)^*\)
At least for positive values of the argument, the Nemtsov function grows monotonously.
The monotonous growth is also property of the inverse function ArqNem, that of the Abelfunction AuNem and that of the real iterates of the Nemtsov function.
For any non-trivial entire function, the inverse function \(\mathrm{ArqNem}_q\) has the branch points.
Two of them are complex; and one of them is expressed with function NemBran.
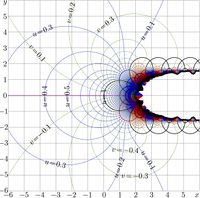
Parametric plot of function NemBran is shown at first picture in figure 4.
At \(z=\mathrm{NemBran}(q)\), function \(\mathrm{ArqNem}_q(z)\) has infinite derivative.
For construction of the inverse function, important are the complex soluitons \(A\) of equation \(\mathrm{Nem}_q^{\prime}=0\).
One of these solutions is expressed with function NemBra, id est, \(A=\mathrm{NemBra}(q)\).
Parametric plots of functions NemBra and NemBran are shown in figure 5;
\(\mathrm{NemBran}(q)=\mathrm{Nem}_q\big(\mathrm{NemBra}(q)\big)\) :
\( \left( \begin{array}{cc} x=\mathrm{Re}\big(\mathrm{NemBran}(q)\big) \\ y=\mathrm{Im}\big(\mathrm{NemBran}(q)\big) \end{array}\right) ~\), left and \(~ \left( \begin{array}{cc} x=\mathrm{Re}\big(\mathrm{NemBra}(q)\big) \\ y=\mathrm{Im}\big(\mathrm{NemBra}(q)\big) \end{array}\right) ~\) , right.
For positive \(q\), both real and imaginary parts of the branchpoint are significantly smaller than unity.
As function NemBra is implemented, the efficient algorithm for evaluation of the inverse functions of the Nemtsov function
can be constructed.
Three of them are denoted with symbols «ArcNem», «ArkNem», «ArqNem».
One of them (ArqNem) is described in the next section.
Inverse function
The Nemtsov function has various inverse functions, as equation
\(\mathrm{Nem}_q(A)=z\)
has many solutions \(A\) ; there are three solutions for \(q\!=\!0\) and four for \(q\!\ne\!0\).
The holomorphic inverse function unavoidably has the cut lines.
The appropriate choice of these cut lines happens to be non–trivial problem.
For construction of the Abelfunction, denoted as AuNem, the special inverse function ArqNem of the Nemtsov function is chosen.
For function ArqNem, the cut lines are chosen in the following way.
One cut line goes along the negative part of the real axis from \(-\infty\) to zero.
Two other cut lines go straightly from zero to the complex branchpoints \(Z_{\mathrm o}\) of the inverse function.
These brach points can be expressed in the following way:
\(Z_{\mathrm o}=\mathrm{Nem}_q(z_{\mathrm{o}})\)
where \(z_{\mathrm o}=\mathrm{NemBran}(q)\) is solution of equation
\(\mathrm{Nem}_q^{\prime}( z_{\mathrm o})=0\)
The following relation takes place:
\(\mathrm{NemBran}(q)=\mathrm{Nem}_q\big(\mathrm{NemBra}(q)\big)\)
Parametric plot of function NemBran is shown in figure 5:
\(x=\mathrm{Re}\big(\mathrm{NemBran}(q)\big)~\),
\(y=\mathrm{Im}\big(\mathrm{NemBran}(q)\big)~\)
At small values of the argument, the Nemtsov function looks similar to the identity function; so, the parametric plot of function NemBran in figure 5 looks similar to that of function NemBra in figure 4.
Complex map of function ArqNem is shown in figure 6 for \(q\!=\!0~\) and in figure 7 for \(q\!=\!2~\):
\(u\!+\!\mathrm i v= \mathrm{ArqNem}_q(x\!+\!\mathrm i y)\)
The complex double implementation of function ArqNem is loaded as arqnem.cin.
In the implementation, parameter \(q\) is stored in the global variable \(Q\). Perhaps, it would not be a good solution for any software,
but this happen to be a simplest way to plot pictures for book «Superfunctions» [1].
Before evaluation of \(\mathrm{ArqNem}_q\) of complex argument, the complex branch point should be evaluated with routine nembran.cin and stored in the global variables tr and ti; in the version from year 2015, the real and imaginary parts of the branch point are stored as two global variables. At any change of parameter \(q\), these values should be recalculated.
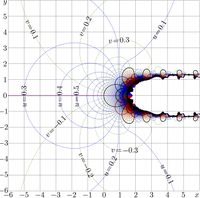
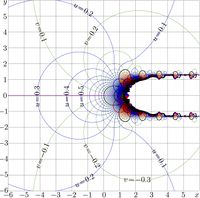
Superfunction
For the Nemtsov function \(\mathrm{Nem}_q\), the superfunction \(\mathrm{SuNem}_q~\) is real–holomorphic solution \(F\) of the transfer equation
\(F(z\!+\!1)=\mathrm{Nem}_q\big( F(z)\big)\)
with specific asymptotic behaviour at infinity, namely,
\(\displaystyle F(z)=\frac{1}{\sqrt{-2 z}}\left( 1-\frac{q}{\sqrt{-2 z}} + O\big( \ln(-z)/z\big) \right)\)
In order to specify function SuNem, the additional condition is assumed:
\(\mathrm{SuNem}_q(0)=1\)
(Similar condition is used to specify tetration as superfunction of exponent).
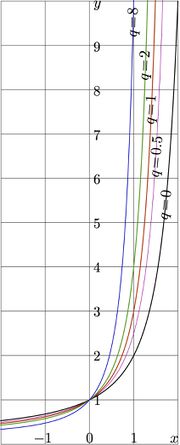
Explicit plot of function SuNem of the real argument is shown in figure at left, \(y\!=\!\mathrm{SuNem}_q(x)\) is plotted versus \(x\) for various values of \(q\).
Function SuNem grows monotonously from zero at \(-\infty\), takes value unity at zero and then grows quickly to infinity for positive values of the argument.
The larger is parameter \(q\), the faster is the growth at \(+\infty\).
This behaviour corresponds to the intuitive expectations about this function.
Complex maps of function SuNem are shown in figures at right for \(q\!=\!0\), \(q\!=\!1\) and for \(q\!=\!2\);
\(u\!+\!\mathrm i v=\mathrm{SuNem}_q(x\!+\!\mathrm i y)\)
Maps for different values of \(q\) look similar; however, the greater is \(q\), the faster is the growth of \(\mathrm{SuNem}_q\) along the real axis.
This is seen also at the explicit plot in figure at left.
In order to construct function SuNem, first, any superfunction \(F\) with appropriate asymptotic behaviour is constructed.
Then, \(\mathrm{SuNem}_q(z)=F(x_1+z)\) where \(x_1\) is real solution of equation \(F(x_1)=1\).
Abelfunction
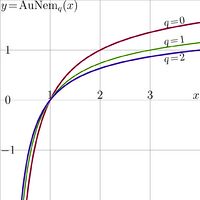
For the Abel function of the Nemtsov function, notation AuNem is suggested.
Explicit plot \(y\!=\!\mathrm{AuNem}_q(x)\) versus \(x\) is shown in figure at left for \(q\!=\!0\), \(q\!=\!1\) and \(q\!=\!2\).
The same plot can be obtained, reflecting the curves for SuNem from the angle bisector of the First quadrant of the coordinate plane.
This property can be used as a mumerical test of relation
\(\mathrm{SuNem}_q(\mathrm{АuNem}_q(x))=x\);
it should be so, while
\(\mathrm{AuNem}_q=\mathrm{SuNem}_q^{-1}\)
As inverse of the superfunction, function AuNem satisfies the Abel equation
\(\mathrm{AuNem}_q\big( \mathrm{Nem}_q(z)\big)=\mathrm{AuNem}_q(z)+1\)
Function AuNem satisfies also the additional condition
\(\mathrm{AuNem}_q(1)=0\)
that is determined by the corresponding property of the SuNem, namely, that \(\mathrm{SuNem}_q(0)\!=\!1~\).
The asymptotic expansion of function AuNem at zero can be found, inverting the asymptotic expansion of function SuNem at \(-\infty\);
the coeffcieints of this expansion can be found also from the Abel equation.
The expansion can be written as follows:
Iterates of the Nemtsov function
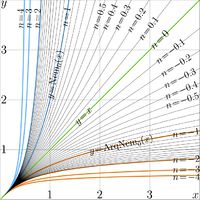
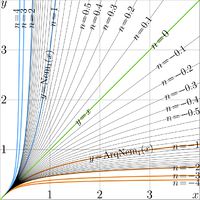
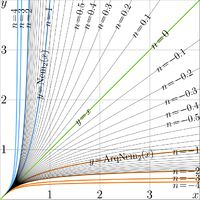
With functions SuNem and AuNem, the \(n\)th iterate of the Nemtsov function can be expressed as follows
\(\mathrm{Nem}_q^{\,n}(z)=\mathrm{AuNem}_q\big( n+\mathrm{AuNem}_q(z)\big)\)
For
\(q\!=\!0\),
\(q\!=\!1\) and for
\(q\!=\!2\),
these iterates are shown in figures at right.
These iterates look similar to other iterates of the fast growing functions.
At positive number \(n\) of iterate, the iterate shows the fast growth; at negative values of \(n\), the growth is slow.
The zeroth iterate (\(n\!=\!0\)), the iterates apperas as identity function.
In the figures, the corresponding graphics are marked with green lines.
Due to the singularity of function ArqNem at zero, the non-integer iterates are not defined at zero and the negative part of the real axis, although they approach zero as the positive argument of the iterate becomes small.
The curves of the iterates show the symmetry with respect to reflections from the bisectris of the First quadrant of the coordinate plane, as
\(\mathrm{Nem}_q^{-n}(z)=\mathrm{ArqNem}_q^{\,n}(z)\)
Application and the Discussion
The Nemtsov function is considered as a candidate of the transfer function, for which the superfunction and the Abel function are diffucult to construct with the exotic iterate at its fixed point zero.
Indeed, the construction required certain efforts, but they sere related mainly with construction of the inverse function ArqNem, the efficient implementation and, especially, with guessing, that namely ArqNem shouls be used to get the Abel function and non–integer iterates, that are holomorphic in the most of the complex plane.
For the Nemtsov function, two other inverse functions have been constructed, they are denoted with hames
ArcNem and ArkNem.
They have different positions of the cut lines, and, at the iterates, do not provide the
holomorphic Abel function.
Once the iterates of the inverse function leads to the fixed point of the transfer function, the exotic iterates are straightforward.
Other transfer functions can be considered in the similar way, assuming, that their expansion at the fixed point begins with the identity function and the cubic term.
Without loss of generality, the coefficient at the cubic term can be treated as unity; the corresponding transform to this case is shown in the last row of the
Table of superfunctions.
Warning
The name «Nemtsov function» is chosen as a simplest mnemonic that refers to the history of century 21.
The naming is not an attempt to remind the Russian usurper and his crime accomplices that
it is not a good style, to kill the political opponent.
The growth of corruption [3] at putin's pahanat indicates that no any moral criteria nor moral concepts can be applied to Russia usurper and his accomplices.
So, the attempt mentioned would be just wane.
However, Editor keeps his right to call things in the most convenient and efficient system of notations.
References
- ↑ 1.0 1.1
https://www.amazon.co.jp/-/en/Dmitrii-Kouznetsov/dp/6202672862
https://www.morebooks.de/shop-ui/shop/product/978-620-2-67286-3
https://mizugadro.mydns.jp/BOOK/468.pdf
Dmitrii Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020. - ↑ https://mizugadro.mydns.jp/PAPERS/2016nemtsov.pdf Dmitrii Kouznetsov. Nemtsov function and its iterates. Mizugadro Preprint, 2016.
- ↑ 3.0 3.1 http://kremlin.ru/transcripts/1566 Д.Медведев. Вступительное слово на заседании Совета по противодействию коррупции. 30 сентября 2008 года, 16:25 Москва, Кремль. Д.Медведев: Коррупция в нашей стране приобрела не просто масштабный характер, она стала привычным, обыденным явлением, которое характеризует саму жизнь в нашем обществе...
2016. http://mizugadro.mydns.jp/2016NEMTSOV/TRY00/23.pdf Dmitrii Kouznetsov. Nemtsov function and its iterates. 2016, Mizugadro Preprint.
Keywords
«Abel function», «ArqNem», «AuNem», «Book», «C++», «Exotic iterate», «Exotic iteration», «Latex», «Mathematica», «Nemtsov function», «Putin killed Nemtsov», «SuNem», «Superfunction», «Superfunctions», «Table of superfunctions»,