Difference between revisions of "File:Qexpmap.jpg"

From TORI
Jump to navigation Jump to search
 
(2 intermediate revisions by the same user not shown)
Line 1: Line 1:
  +
{{oq|Qexpmap.jpg|Original file ‎(682 × 706 pixels, file size: 152 KB, MIME type: image/jpeg)}}
⚫
[[Complex map]] of function [[square root of exponential]], \( \varphi=\sqrt{\exp} \)
  
  +
  ⚫
[[Complex map]] of function «[[square root of exponential]]», \( \varphi=\sqrt{\exp} \),
  +
from article «[[Superfunctions and square root of factorial]]»
 
<ref name="factorial">
  
<ref name="factorial">
 
https://link.springer.com/article/10.3103/S0027134910010029 <br>
  
https://link.springer.com/article/10.3103/S0027134910010029 <br>
Line 5: Line 8:
 
https://mizugadro.mydns.jp/PAPERS/2010superfar.pdf (Russian)<br>
  
https://mizugadro.mydns.jp/PAPERS/2010superfar.pdf (Russian)<br>
 
D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12. (Russian version: p.8-14)
  
D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12. (Russian version: p.8-14)
  +
</ref>. In the article, the [[square root of exponential]] (shown in the map) is compared to the [[square root of factorial]].
⚫
</ref>
  
   
 
Function \( \varphi(z) = \mathrm{tet}(1/2+\mathrm{ate}(z)) = \exp^{1/2}(z)\)
  
Function \( \varphi(z) = \mathrm{tet}(1/2+\mathrm{ate}(z)) = \exp^{1/2}(z)\)
Line 18: Line 21:
 
<ref>
  
<ref>
 
http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi [[Hellmuth Kneser]]. Reelle analytische Lösungen der Gleichung \( φ(φ(x))=e^x \) und verwandter Funktionalgleichungen. Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67
  
http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi [[Hellmuth Kneser]]. Reelle analytische Lösungen der Gleichung \( φ(φ(x))=e^x \) und verwandter Funktionalgleichungen. Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67
  ⚫
</ref>.
  +
  +
Natural [[Tetration]] \(\mathrm{tet}\) and
  +
[[Arctetration]] \(\mathrm{ate}\!=\!\mathrm{tet}^{-1}\)
  +
are implemented in 2009-2010 <ref>
  +
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html <br>
  +
https://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf
  +
D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670.
  +
Preprint: 2009analuxpRepri.pdf
  +
</ref><ref>
  +
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html <br>
  +
https://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf
  +
D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670.
 
</ref>
  
</ref>
  +
and described in book «[[Superfunctions]]»
  +
<ref>
  +
https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. [[Superfunctions]]: Non-integer iterates of holomorphic functions. [[Tetration]] and other [[superfunction]]s. Formulas,algorithms,tables,graphics ペーパーバック – 2020/7/28
  +
</ref><ref>https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). [[Superfunctions]]: Non-integer iterates of holomorphic functions. [[Tetration]] and other [[superfunction]]s. Formulas, algorithms, tables, graphics. Publisher: [[Lambert Academic Publishing]].
  +
</ref> (chapters 14 and 15), similar map appears in the left part of figure 15.5 at page 211 for iterate \(n\!=\!0.5\ \).
  +
  +
==Misprint==
  +
  +
There is a misprint in this map:
  +
  +
\( p=-1.6 \)
  +
  +
appears instead of correct
  +
  +
\( p=-0.6 \)
  +
  +
==Improved version==
  +
  +
The improved (and corrected) version of this map is loaded as
  +
  +
https://mizugadro.mydns.jp/t/index.php/File:QexpMap1263x1243.png
  +
 
==References==
  
==References==
  +
{{ref}}
−
<references/>
  
  +
  +
{{fer}}
  +
==Keywords==
  +
  +
«[[Abelfunction]]»,
  +
<b>«[[ArcTetration]]»</b>,
  +
«[[Book]]»,
  +
«[[BookMap]]»,
  +
<b>«[[Hellmuth Kneser]]»</b>,
  +
«[[Iterate]]»,
  +
«[[Iteration half of exponential]]»,
  +
«[[Iteration half of factorial]]»,
  +
«[[Natural tetration]]»,
  +
<b>«[[Square root of exponential]]»</b>,
  +
«[[Square root of factorial]]»,
  +
«[[Superfunction]]»,
  +
«[[Superfunctions]]»,
  +
«[[Tetration]]»,
   
 
[[Category:Abelfunction]]
  
[[Category:Abelfunction]]
Line 26: Line 82:
 
[[Category:Book]]
  
[[Category:Book]]
 
[[Category:BookMap]]
  
[[Category:BookMap]]
  +
[[Category:Complex map]]
 
[[Category:Hellmuth Kneser]]
  
[[Category:Hellmuth Kneser]]
 
[[Category:Iterate]]
  
[[Category:Iterate]]
  +
[[Category:Iteration half of exponential]]
  +
[[Category:Misprint]]
  +
[[Category:Natural tetration]]
 
[[Category:Superfunction]]
  
[[Category:Superfunction]]
 
[[Category:Tetration]]
  
[[Category:Tetration]]

Latest revision as of 12:58, 14 December 2025


Complex map of function «square root of exponential», \( \varphi=\sqrt{\exp} \), from article «Superfunctions and square root of factorial» [1]. In the article, the square root of exponential (shown in the map) is compared to the square root of factorial.

Function \( \varphi(z) = \mathrm{tet}(1/2+\mathrm{ate}(z)) = \exp^{1/2}(z)\)

appears as solution of equation

\( \varphi(\varphi(z))=\exp(z) \)

Existence of this function is shown in 1950 by Hellmuth Kneser [2].

Natural Tetration \(\mathrm{tet}\) and Arctetration \(\mathrm{ate}\!=\!\mathrm{tet}^{-1}\) are implemented in 2009-2010 [3][4] and described in book «Superfunctions» [5][6] (chapters 14 and 15), similar map appears in the left part of figure 15.5 at page 211 for iterate \(n\!=\!0.5\ \).

Misprint

There is a misprint in this map:

\( p=-1.6 \)

appears instead of correct

\( p=-0.6 \)

Improved version

The improved (and corrected) version of this map is loaded as

https://mizugadro.mydns.jp/t/index.php/File:QexpMap1263x1243.png

References

  1. ↑ https://link.springer.com/article/10.3103/S0027134910010029
    https://mizugadro.mydns.jp/PAPERS/2010superfae.pdf (English)
    https://mizugadro.mydns.jp/PAPERS/2010superfar.pdf (Russian)
    D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12. (Russian version: p.8-14)
  2. ↑ http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi Hellmuth Kneser. Reelle analytische Lösungen der Gleichung \( φ(φ(x))=e^x \) und verwandter Funktionalgleichungen. Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67
  3. ↑ http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
    https://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670. Preprint: 2009analuxpRepri.pdf
  4. ↑ http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
    https://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670.
  5. ↑ https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics ペーパーバック – 2020/7/28
  6. ↑ https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.

File history

Click on a date/time to view the file as it appeared at that time.

Date/TimeThumbnailDimensionsUserComment
current21:48, 30 November 2019Thumbnail for version as of 21:48, 30 November 2019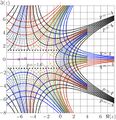682 × 706 (152 KB)T (talk | contribs)

You cannot overwrite this file.

The following 3 pages use this file:

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Retrieved from "https://mizugadro.mydns.jp/t/index.php?title=File:Qexpmap.jpg&oldid=46232"