File:SuTraAsyQ2ateT.png
Original file (644 × 1,235 pixels, file size: 28 KB, MIME type: image/png)
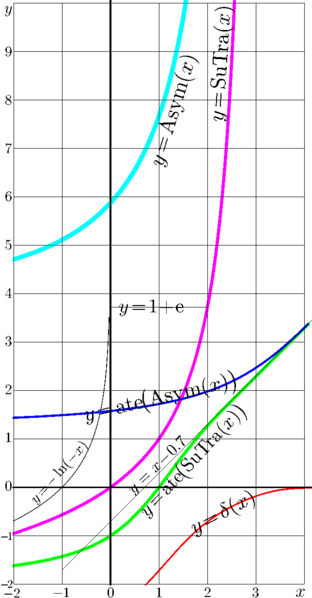
Explicit plot of the generalyzed Asymptotic «Asym» (thick light blue (Cyan) curve) of function SuTra (pink curve) through the growing SuperExponential to base \(\sqrt{2}\) and the related functions.
Asymptotic statement
For real \(x\to +\infty\), \(x>0\), \[ \mathrm{SuTra}(x) \ \underset{\overset{x\to+\infty}{x>0}}{\overset{\mathrm{ate}}{\sim}} \mathrm{Asym}(x) \, , \qquad \mathrm{Asym}(x)= \mathrm{SuExp}_{\sqrt{2},4,5}(x+x_{\mathrm{stq2}}), \] where the shift constant is numerically estimated as \[ x_{\mathrm{stq2}}\approx 1.219 \]
By definition, this means \[ \lim_{x\to+\infty} \Big( \mathrm{ate}\!\big(\mathrm{SuTra}(x)\big) - \mathrm{ate}\!\big(\mathrm{Asym}(x)\big) \Big) =0. \]
Description of the curves
Pink curve: \(\ y=\mathrm{SuTra}(x)\), the superfunction of the Trappmann map \(z\mapsto z+\exp z\). SuTra is Entire Function with Logarithmic Asymptotic, it is described at the Applied Mathematical Sciences [1], 2013.
Light blue (cyan) curve: \(\ y=\mathrm{Asym}(x) = \mathrm{SuExp}_{\sqrt{2},4,5}(x\!+\!x_{\mathrm{stq2}}) \) . This is ArctetralAsymptotic of function SuTra with growing SuperExponential to base \(\sqrt{2}\) at large input. This growing SuperExponential \(\mathrm{SuExp}_{\sqrt{2},4,5}\) is described at Mathematics of Computation [2], 2010. In this calculus, the following evaluate of the parameter is used: \( x_{\mathrm{stq2}}\!\approx\! 1.219 \ \). In the routine below, identifier "Shift" is used for this parameter. The last digit of this estimate is subject for the revision (and perhaps the correction).
Green curve: \(\ y=\mathrm{ate}\!\big(\mathrm{SuTra}(x)\big)\), the ArcTetrational "image" of SuTra. The natural ArcTetration \(\mathrm{ate}\) is described at Mathematics of Computation [3], 2009; the efficient implementations of the natural tetration \(\mathrm{tet}\) and that of the natural ArcTetration \(\mathrm{ate}\) are described at Vladikavkaz Mathematical Journal [4], 2010. Even improved algorithms to evaluate the tetration and arctetration are suggested also by William Paulsen and Samuel Patrick Cowgill [5][6][7], but, up to year 2026, the C++ implementations for these algorithms are not found in the free access.
Thin black curve at the left hand side: \( y=-\ln(-x)\), it is asymptotic of function SuTra at large negative input.
Dark blue curve: \(\ y=\mathrm{ate}\!\big(\mathrm{Asym}(x)\big)\), the ArcTetrational image of the asymptotic function.
The functions mentioned above (except the «Asym») are described also in book «Superfunctions» [8], 2014,2020.
The green and blue curves approach the same straight line, indicating the asymptotic equivalence. This line is approximated with \(\ y=x\!-\!0.7 \ \).
Red curve: \( \ y=\delta(x) \ \); it is arctetral residual \(\ \delta(x)= \mathrm{ate}\!\big(\mathrm{SuTra}(x)\big) - \mathrm{ate}\!\big(\mathrm{Asym}(x)\big)\, \); it tends to zero and quantifies the precision of the asymptotic approximation.
The additional short grid line \(\ y=\mathrm e\!+\!1 = \mathrm{SuTra}(2) \ \) marks the specific value of the SuperTrappmann function at the integer input.
C++
/* subroutines ado.cin, Tania.cin, LambertW.cin, SuZex.cin, fslog.cin should be loaded in order to compile the source below.*/
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include<complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "Tania.cin" // need for LambertW
#include "LambertW.cin" // need for AuZex
#include "SuZex.cin"
#include "Sqrt2f45e.cin"
#include "Sqrt2f45l.cin"
#include "fslog.cin"
z_type tra(z_type z){ return exp(z)+z;}
z_type sutra(z_type z){ if( Re(z)<2. || fabs(Im(z))>2. ) return log(suzex(z));
return tra(sutra(z-1.));}
DB Shift=1.219;
z_type Asym(z_type z){ return F45E(z+Shift); }
#include "ado.cin"
#define M(x,y) fprintf(o,"%6.4f %6.4f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%6.4f %6.4f L\n",0.+x,0.+y);
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
FILE *o;o=fopen("SuTraAsyQ2ate.eps","w"); ado(o,622,1212); fprintf(o,"202 202 translate\n 100 100 scale 1 setlinejoin 2 setlinecap\n");
DO(m,411){x=-2.02+.02*m; y=Re(sutra(x)); if(m==0) M(x,y) else L(x,y) if(x>6.03||y>10) break;} fprintf(o,".06 W 1 0 1 RGB S\n");
DO(m,100){x=-2.01+.02*m; y=-log(-x); if(m==0) M(x,y) else L(x,y) if(x>6.03||y>10) break;} fprintf(o,".01 W 0 0 0 RGB S\n");
DO(m,720){x=-2.1+.01*m; z=sutra(x);
if(!(abs(z)<1.e32)) {
// printf("%lg %lg %lg\n",x,Re(z),Im(z));
break;
}
z=FSLOG(z); y=Re(z); //printf("%6.3lf %16.14lf \n",x,Re(z));
if(m==0) M(x,y) else L(x,y) if(x>4.4||y>10) break;
} fprintf(o,".06 W 0 1 0 RGB S\n");
DO(m,720){x=-2.1+.01*m; z=Asym(x);
if(!(abs(z)<1.e32)) { // printf("%lg %lg %lg\n",x,Re(z),Im(z));
break; }
// z=F45L(z); y=Re(z);
z=FSLOG(z); y=Re(z); //printf("%6.3lf %16.14lf \n",x,Re(z));
if(m==0) M(x,y) else L(x,y) if(x>4.4||y>10) break;
} fprintf(o,".04 W 0 0 1 RGB S\n");
DO(m,637){x=-2.1+.01*m; c=FSLOG(sutra(x)); d=FSLOG(Asym(x)); y=Re((c-d)); if(m==0) M(x,y) else L(x,y); }
fprintf(o,".03 W 1 0 0 RGB S\n");
DO(m,84){ x=-2.1+.1*m; z=Asym(x); y=Re(z); if(m==0) M(x,y) else L(x,y); if(y>10) break; } fprintf(o,".09 W 0 1 1 RGB S\n");
for(n=-2;n<11;n++) {M(-2,n)L(4,n)}
for(m=-2;m<5;m++) {M(m,-2)L(m,10)} M(0,1.+M_E) L(2,1.+M_E)
M(-1,-1.7)L(5,5-.7)fprintf(o,"0 0 0 RGB .004 W S\n");
M(0,-2.1)L(0,10.1)
M(-2.1,0)L(6.1,0) fprintf(o,".03 W S\n");
fprintf(o,"showpage\n"); fprintf(o,"%c%cTrailer\n",'%','%'); fclose(o);
system("epstopdf SuTraAsyQ2ate.eps");
system( "open SuTraAsyQ2ate.pdf"); //for macintosh
return 0;
Latex
\documentclass[12pr]{article}
\paperwidth 646pt
\paperheight 1240pt
\textwidth 800pt
\textheight 1700pt
\topmargin -96pt
\oddsidemargin -66pt
%\usepackage{xcolor}
\usepackage{graphicx}
\usepackage{rotating}
\newcommand \sx {\scalebox}
\newcommand \ing {\includegraphics}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\parindent 0pt
\begin{document}
\begin{picture}(720,1220)
%\put(-2,-6){\textcolor{white}{\rule{740pt}{740pt}}}
%\put(20,20){\ing{SuTraAsy3plot}}
%\put(20,20){\ing{SuTraAsyQplot}}
\put(20,20){\ing{SuTraAsyQ2ate}}
\put( 3,1206){\sx{3.2}{\(y\)}}
\put( 4,1116){\sx{3}{\(9\)}}
\put( 4,1016){\sx{3}{\(8\)}}
\put( 4,916){\sx{3}{\(7\)}}
\put( 4,816){\sx{3}{\(6\)}}
\put( 4,716){\sx{3}{\(5\)}}
\put( 4,616){\sx{3}{\(4\)}}
\put(240,585){\sx{4}{\(y\!=\!1\!+\!\mathrm e\)}}
\put( 4,516){\sx{3}{\(3\)}}
\put( 4,416){\sx{3}{\(2\)}}
\put( 4,316){\sx{3}{\(1\)}}
\put( 4,216){\sx{3}{\(0\)}}
\put(-6,114){\sx{2.4}{\(-\!1\)}}
\put(-6,14){\sx{2.4}{\(-\!2\)}}
\put(0,-6){\sx{2.8}{\(-2\)}}
\put(102,-5){\sx{2.9}{\(-1\)}}
\put(216,-5){\sx{3}{\(0\)}}
\put(316,-5){\sx{3}{\(1\)}}
\put(416,-5){\sx{3}{\(2\)}}
\put(516,-5){\sx{3}{\(3\)}}
\put(606,-4){\sx{3.6}{\(x\)}}
%\put(190,356){\sx{3}{\rot{83}\(y\!=\!-\ln(-x)\)\ero}}
\put(68,188){\sx{3}{\rot{48}\(y\!=\!-\ln(-x)\)\ero}}
\put(330,886){\sx{4.5}{\rot{73}\(y\!=\!\mathrm{Asym}(x)\)\ero}}
\put(455,980){\sx{4.4}{\rot{86}\(y\!=\!\mathrm{SuTra}(x)\)\ero}}
\put(170,360){\sx{4.4}{\rot{13}\(y\!=\!\mathrm{ate}\!\big(\mathrm{Asym}(x)\big)\)\ero}}
%\put(488,728){\sx{5}{\rot{85}\(y\!=\!\mathrm{SuTra}(x)\)\ero}}
%\put(24,119){\sx{3}{\rot{22}\(y\!=\!\mathrm{SuTra}(x)\)\ero}}
%\put(488,633){\sx{3.4}{\rot{44}\(y=x\!+\!x_{\mathrm{ste2}}\)\ero}}
\put(270,208){\sx{3.4}{\rot{44}\(y=x\!+\!0.7\)\ero}}
\put(298,160){\sx{4}{\rot{47}\(y\!=\!\mathrm{ate}\!\big(\mathrm{SuTra}(x)\big)\)\ero}}
%\put(440,56){\sx{4}{\rot{84}\(y\!=\!\mathrm{AuExp_{\sqrt{2},4,5}}\big(\mathrm{SuTra}(x)\big)\)\ero}}
%\put(528,62){\sx{3}{\rot{70}\(y=10 \ \delta(x)\)\ero}}
\put(396,125){\sx{4.4}{\rot{28}\(y\!=\!\delta(x)\)\ero}}
\end{picture}
\end{document}
References
- ↑
http://www.m-hikari.com/ams/ams-2013/ams-129-132-2013/kouznetsovAMS129-132-2013.pdf
https://mizugadro.mydns.jp/PAPERS/2013hikari.pdf D.Kouznetsov. Entire Function with Logarithmic Asymptotic. Applied Mathematical Sciences, 2013, v.7, No.131, p.6527-6541. - ↑
http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
https://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf
https://mizugadro.mydns.jp/PAPERS/2010q2.pdf D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756. - ↑
https://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
https://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670. - ↑
https://www.vmj.ru/articles/2010_2_4.pdf (in Russian)
https://mizugadro.mydns.jp/PAPERS/2010vladie.pdf (English version) D.Kouznetsov. Tetration as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45. - ↑ https://arch.astate.edu/cgi/viewcontent.cgi?article=1561&context=all-etd 4-20-2017 Exploring Tetration in the Complex Plane Samuel Patrick Cowgill
- ↑ https://dl.acm.org/doi/abs/10.1007/s10444-017-9524-1 William Paulsen, Samuel Cowgill. Solving F(z + 1) = bF(z) in the complex plane // Advances in Computational Mathematics, Volume 43, Issue 6 Pages 1261 - 1282
- ↑ https://arch.astate.edu/scm-mathfac/9/ Paulsen, William and Cowgill, Samuel, "Solving F(z + 1) = b F(z) in the complex plane" (2017). Faculty Publications. 9.
- ↑
https://mizugadro.mydns.jp/BOOK/202.pdf (Russian version, 2014)
https://mizugadro.mydns.jp/BOOK/468.pdf (Engish version, 2020). Dmitrii Kouuznetsov. Superfunctions. Lambert Academic Publishing, 2020
Keywords
«Abelfunction», «Approximation», «Arctetral asymptoric», «Asymptotic», «Base sqrt2», «Logarithmic asymptotic», «Natural ArcTetration», «SuperExponential», «Superfunction», «Superfunctions», «SuTra», «Trappmann function»,
«Суперфункции»,
«ado.cin», «fsexp.cin» (C++ implementation of natural tetration), «fslog.cin» (C++ implementation of natural ArcTetration), «Tania.cin», «LambertW.cin», «SuZex.cin» (Function SuTra is implemented through function SuZex\( = z\mapsto z\ \exp(z)\)), «Sqrt2f45e.cin» (C++ implementation of growing SuperExponential to base sqrt2), «Sqrt2f45l.cin» (C++ implementation of growing AbelExponential to base sqrt2)
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 09:41, 5 February 2026 |  | 644 × 1,235 (28 KB) | T (talk | contribs) | misprint, there was wrong sign in formula y=x-0.7 |
| 16:13, 4 February 2026 |  | 644 × 1,235 (28 KB) | T (talk | contribs) | {{oq|SuTraAsyQ2ateT.png|Original file (644 × 1,235 pixels, file size: 28 KB, MIME type: image/png)|600}} Atemptotic Asym (thick light blue curve) of function SuTra (pink curve) through the growing SuperExponential to base \(\sqrt{2}\). Here, term Atemptotic means the Restrict asymptotic with natural ArcTetration \(\mathrm{ate}\) as the Criterion function. \[ \mathrm{SuTra}(x)\ \underset{\overset{x\to +\infty}{x>0}}{{\overset{\mathrm{ate}}{\Larg... |
You cannot overwrite this file.
File usage
The following page uses this file: