File:QfacMapT500a.jpg

Original file (2,352 × 2,352 pixels, file size: 1.99 MB, MIME type: image/jpeg)
Complex map of function square root of factorial, or \(\sqrt{!}\), or halfiteration of factorial.
\[h=\mathrm{Factorial}^{1/2}\]
is such function that \(\ h(h(z)) = z!\ \) in wide range of values of \(z\).
Levels \(u=\Re(h(z))=\rm const\) and Levels \(u=\Im(h(z))=\rm const\) are shown in the plane \(\ z=x\!+\!\mathrm i y\ \).
Iterates of Factorial are implemented through the Superfunciton AuFac and the Abelfunction SuFac:
\[ \mathrm{Factorial}^n(z)=\mathrm{SuFac}\big(n+\mathrm{AuFac}(z)\big) \]
These functions are described in the Moscow University Physics Bulletin, 2010 [1].
This map is used as Fig.8.10 at page 101 of book «Superfunctions»[2][3]
in order to give meaning to the logo
of the Physics Department of the Moscow State University
and also to show how the iterates of a real-holomorphic function look like.
C++ generator of curves
// In order to compile the code below, the following files should be loaded in the working directory: // fac.cin , // facp.cin , // afacc.cin , // superfac.cin , // arcsuperfac.cin , // ado.cin , // conto.cin
// #include <math.h>
#include <stdio.h>
#include <stdlib.h>
using namespace std;
#include <complex>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "fac.cin"
#include "facp.cin"
#include "afacc.cin"
#include "superfac.cin"
#include "arcsuperfac.cin"
//#include "superex.cin"
//#include "superlo.cin"
DB xL=0.31813150520476413;
DB yL=1.3372357014306895;
#include "conto.cin"
int main(){ int j,k,m,n,n1; DB x,y, p,q, t; z_type z,c,d;
int M=400,M1=M+1;
int N=401,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
FILE *o;o=fopen("qfacMap.eps","w");ado(o,402,402);
fprintf(o,"201 201 translate\n 20 20 scale\n");
DO(m,M1) X[m]=-8.+.04*m;
DO(n,N1){ y=-8.+.04*n; if(y<-.011) Y[n]=y; else break;}
Y[n]= -.01; n++;
Y[n]= +.01; n++;
for(j=n;j<N1;j++){y=-8.+.04*(j-1); Y[j]=y;}
for(m=-8;m<9;m++){if(m==0){M(m,-8.5)L(m,8.5)} else{M(m,-8)L(m,8)}}
for(n=-8;n<9;n++){ M( -8,n)L(8,n)}
fprintf(o,".008 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){g[m*N1+n]=9999; f[m*N1+n]=9999;}
DO(m,M1){x=X[m]; printf("%5.2f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y);
// c=afacc(z);
// c=fac(c);
c=arcsuperfac(z);
c=superfac(.5+c);
// c=FSLOG(z);
// c=FSEXP(.5+c);
// d=z;
// p=abs(c-d)/(abs(c)+abs(d)); p=-log(p)/log(10.)-1.;
p=Re(c);q=Im(c);
if(p>-999 && p<999) g[m*N1+n]=p;
if(q>-999 && q<999 && fabs(q)> 1.e-14) f[m*N1+n]=q;
}}
fprintf(o,"1 setlinejoin 1 setlinecap\n"); //p=6.;q=6.;
//#include"plofu.cin"
p=1;q=.5;
for(m=-2;m<2;m++) for(n=1;n<10;n+=1)conto(o,f,w,v,X,Y,M-20,N,(m+.1*n),-q, q); fprintf(o,".02 W 0 .6 0 RGB S\n");
for(m= 0;m<2;m++) for(n=1;n<10;n+=1)conto(o,g,w,v,X,Y,M-20,N,-(m+.1*n),-q, q); fprintf(o,".02 W .9 0 0 RGB S\n");
for(m= 0;m<2;m++) for(n=1;n<10;n+=1)conto(o,g,w,v,X,Y,M-20,N, (m+.1*n),-q, q); fprintf(o,".02 W 0 0 .9 RGB S\n");
for(m=1;m<5;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p); fprintf(o,".04 W .9 0 0 RGB S\n");
for(m=1;m<5;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".04 W 0 0 .9 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-p,p); fprintf(o,".04 W .6 0 .6 RGB S\n");
for(m=-4;m<5;m++) conto(o,g,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".04 W 0 0 0 RGB S\n");
fprintf(o,"0 setlinejoin 0 setlinecap\n");
x=.85;
M(x,0)L(-8.1,0) fprintf(o,".07 W 1 1 1 RGB S\n");
DO(m,22){ M(x-.4*m,0) L(x-.4*(m+.5),0) } fprintf(o,".1 W 0 0 0 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf qfacMap.eps");
system( "open qfacMap.pdf"); // for mac
// getchar(); system("killall Preview"); //for macintosh
//return 0;
}
Latex generator of labels
%\documentclass[12pt]{article}
\usepackage{graphicx}
\usepackage{geometry}
\paperwidth 340pt
\paperheight 340pt
\usepackage{rotating}
\textwidth 800mm
\textheight 400mm
\topmargin -61mm
\oddsidemargin -77pt
\parindent 0pt
\newcommand \sx {\scalebox}
\newcommand \rot \begin{rotate}
\newcommand \ero \end{rotate}
\newcommand \ax {
\put( 10,346){\sx{1.4}{$y$}}
\put( 10,307){\sx{1.3}{$6$}}
\put( 10,267){\sx{1.3}{$4$}}
\put( 10,227){\sx{1.3}{$2$}}
\put( 10,187){\sx{1.3}{$0$}}
\put( 0,147){\sx{1.3}{$-2$}}
\put( 0,107){\sx{1.3}{$-4$}}
\put( 0, 67){\sx{1.3}{$-6$}}
\put( 0, 27){\sx{1.3}{$-8$}}
\put( 50, 17){\sx{1.3}{$-6$}}
\put( 90, 17){\sx{1.3}{$-4$}}
\put(130, 17){\sx{1.3}{$-2$}}
\put(178, 17){\sx{1.3}{$0$}}
\put(218, 17){\sx{1.3}{$2$}}
\put(258, 17){\sx{1.3}{$4$}}
\put(298, 17){\sx{1.3}{$6$}}
\put(334, 17){\sx{1.4}{$x$}}
}
\begin {document}
\begin{picture}(350,420)
%\put(-20,-10){\includegraphics{fig4a}}\ax
\put(-20,-10){\includegraphics{qfacMap}}\ax
\put(20,174){\sx{1.1}{$u$=0}}
\put(66,160){\sx{1.1}{$v$=0}}
\put(101,174){\sx{1.1}{$u$=0}}
\put(132,174){\sx{1.1}{$v$=0}}
{\put(70,187){\sx{1.8}{\bf cut}}}
\put(300,277){\rot{ 10}\sx{1.3}{$u\!=\!-4$}\ero}
\put(310,250){\rot{16}\sx{1.3}{$u\!= 4$}\ero}
\put(300,205){\rot{-7}\sx{1.3}{$v\!= 4$}\ero}
\put(300,172){\rot{ 6}\sx{1.3}{$v\!=\!-4$}\ero}
\put(308,128){\rot{-23}\sx{1.3}{$u\!= 4$}\ero}
\put(300, 99){\rot{-15}\sx{1.3}{$u\!=\!-4$}\ero}
\end{picture}
\end{document}
%
References
- ↑
http://www.springerlink.com/content/qt31671237421111/fulltext.pdf?page=1
http://mizugadro.mydns.jp/PAPERS/2010superfae.pdf English version
http://mizugadro.mydns.jp/PAPERS/2010superfar.pdf Russian version
D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12. (Russian version: p.8-14) - ↑ https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics - Lambert Academic Publishing, 2020/7/28
- ↑ https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.
Keywords
«Abelfactorial», «Abelfunction», «AuFac», «Factorial», «Iterate», «Regular iteration», «SuFac», «Superfactorial», «Superfunction», «Superfunctions», «Square root of factorial»,
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 15:36, 11 July 2013 | 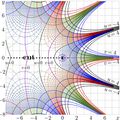 | 2,352 × 2,352 (1.99 MB) | T (talk | contribs) | [[Complex map of function square root of factorial, or $\sqrt{!}$, or halfiteration of factorial $h=\mathrm{Factorial}^{1/2}$ is such function that $ h(h(z)) = z!$ in wide range of values of $z$. Levels $u=\Re(h(z))=\rm const$ and Leve... |
You cannot overwrite this file.
File usage
There are no pages that use this file.