File:AteSuFacMapV.png

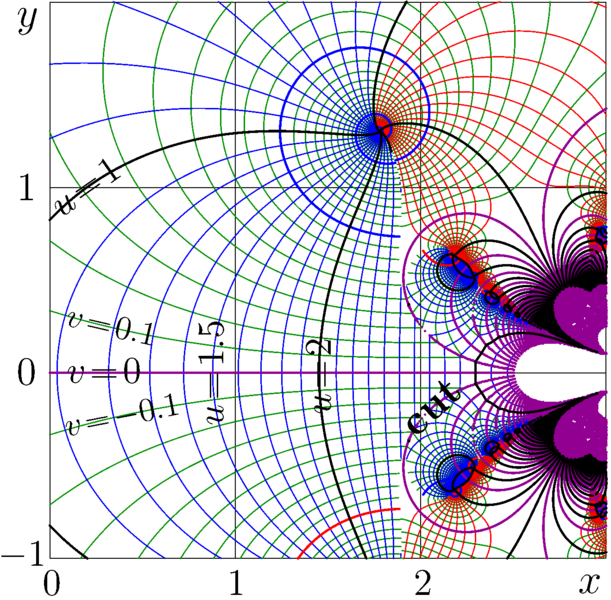
Complex map of combination of natural ArcTetration and SuperFactorial:

\(f(z)=\mathrm{ate}\Big(\mathrm{SuFac}(z)\Big)\)

The map is shown in the top picture with

lines \(u=\Re \big(\mathrm{f}(x\!+\!\mathrm i y)\big)\) and

lines \(v=\Im \big(\mathrm{f}(x\!+\!\mathrm i y)\big)\) in the \(x,y\) plane.

The view of the map hints the conjecture about the asymptotic of SuperFactorial:
there exist parameter \(a>0\) and range \(D\) in vicinity of real axis such that \[ \mathrm{SuFac}(z) \underset{\mathrm{\mathrm{ate}, \ z\in D,\ z\to \infty}}{\sim} \mathrm{tet}(z+a) \] The finger estimates:

\( a \approx 0.7 \)

\( D \approx \{z\in \mathbb C:\ \Re(z)\!>\!0, |\Im(z)|\!<\!\exp(-\Re(z)) \} \)

C++

/* Files ado.cin, Conrec6.cin, fac.cin, SuFac.cin, fslog.cin should be loaded in order to commute the face below.
If saved as «AteSuFacMap.cc», then it is supposed to be compiled with command « c++ -std=c++11 AteSuFacMap.cc -O2 -o AteSuFacMap ».

// c++ -std=c++11 AteSuFacMap.cc -O2 -o AteSuFacMap
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include <complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
 #include"ado.cin"
 #define M(x,y) fprintf(o,"%6.4f %6.4f M\n",1.*(x),1.*(y));
 #define L(x,y) fprintf(o,"%6.4f %6.4f L\n",1.*(x),1.*(y));
#include "Conrec6.cin"
#include "fac.cin"
#include "SuFac.cin"
#include "fslog.cin"
//#include "filog.cin"
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
//int M=971,M1=M+1;
int M=694,M1=M+1;
int N=751,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1];
FILE *o;o=fopen("AteSuFacMap.eps","w");ado(o,308,308);
fprintf(o,"4 104 translate\n 100 100 scale\n");

DO(m,M1) X[m]=0+.00433*(m-.5);
DO(n,N1) Y[n]=-1+.004*(n-.5);

for(m=0;m<4;m++){M(m,-1)L(m,2)}
for(n=-1;n<3;n++){M(0,n)L(3,n)}
fprintf(o,"2 setlinecap .004 W 0 0 0 RGB S\n");
//fprintf(o,".0007 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){g[m+M1*n]=9999; f[m+M1*n]=9999;}
DO(m,M1){x=X[m]; //printf("%5.2f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y); 
// c=Filog(z);
// c=z*z*sin(1./z);
c=superfac(z); //SuFac

if(abs(c)<1.e16 && (x<2.6 || fabs(y)>.1 ) )
{
c=FSLOG(c); // ate
p=Re(c);q=Im(c); 
if(p>-201. && p<201. && q>-201. && q<201. ){ g[m+M1*n]=p;f[m+M1*n]=q;}
}

       }}

printf("Try to plot\n"); // getchar();

fprintf(o,"1 setlinejoin 1 setlinecap\n"); p=.5;q=.4;

for(m=-3;m<4;m++)for(n=1;n<10;n+=1)Conrec6(o,f,X,Y,M1,N1,(m+.1*n), q); fprintf(o,".006 W 0 .6 0 RGB S\n");
for(m=0;m<4;m++) for(n=1;n<10;n+=1)Conrec6(o,g,X,Y,M1,N1,-(m+.1*n), q); fprintf(o,".006 W .9 0 0 RGB S\n");
for(m=0;m<4;m++) for(n=1;n<10;n+=1)Conrec6(o,g,X,Y,M1,N1, (m+.1*n), q); fprintf(o,".006 W 0 0 .9 RGB S\n");
for(m=1;m<4;m++) Conrec6(o,f,X,Y,M1,N1, (0.-m),p); fprintf(o,".012 W .9 0 0 RGB S\n");
for(m=1;m<4;m++) Conrec6(o,f,X,Y,M1,N1, (0.+m),p); fprintf(o,".012 W 0 0 .9 RGB S\n");
                  Conrec6(o,f,X,Y,M1,N1, (0. ),p); fprintf(o,".012 W .6 0 .6 RGB S\n");
for(m=-3;m<4;m++) Conrec6(o,g,X,Y,M1,N1, (0.+m),p); fprintf(o,".012 W 0 0 0 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
     system("epstopdf AteSuFacMap.eps"); 
     system(    "open AteSuFacMap.pdf"); //for mac
}

Latex

\documentclass[12pt]{article}
\usepackage[utf8]{inputenc}
\usepackage[T2A]{fontenc}
\usepackage[russian]{babel}
\usepackage{graphicx}
\usepackage{wrapfig}
\usepackage{hyperref} 
\usepackage{rotating} 
\usepackage[export]{adjustbox}
%\paperwidth 662pt
%\paperheight 650pt
\paperwidth 1324pt
\paperheight 1300pt
\topmargin -124pt
\textheight 1750pt
\oddsidemargin -60pt
\textwidth 1512pt
\newcommand{\ing}{\includegraphics}
\newcommand{\sx}{\scalebox}
\newcommand{\rot}{\begin{rotate}}
\newcommand{\ero}{\end{rotate}}
\parindent 0px
\begin{document}
\sx{4}{\begin{picture}(332,330)
\put(20,20){\ing{AteSuFacMap}}
\put(6,312){\sx{1.9}{\(y\)}}
\put(6,218){\sx{1.8}{\(1\)}}
\put(6,118){\sx{1.8}{\(0\)}}
\put(-4,020){\sx{1.7}{\(-1\)}}
\put(20,4){\sx{1.7}{\(0\)}}
\put(120,4){\sx{1.7}{\(1\)}}
\put(221,4){\sx{1.7}{\(2\)}}
\put(310,05){\sx{1.9}{\(x\)}}
\put(32,150){\sx{1.5}{\rot{-13}\(v\!=\!0.1\)\ero}} 
\put(33,119){\sx{1.7}{\rot{0}\(v\!=\!0\)\ero}} 
\put(33,90){\sx{1.5}{\rot{11}\(v\!=\!-0.1\)\ero}} 

\put(30,208){\sx{1.7}{\rot{35}\(u\!=\!1\)\ero}} 
\put(118,96){\sx{1.7}{\rot{90}\(u\!=\!1.5\)\ero}} 
\put(176,102){\sx{1.7}{\rot{90}\(u\!=\!2\)\ero}} 
\put(222,89){\sx{1.9}{\rot{42}\bf cut\ero}} 
\end{picture}}
\end{document}

References