Difference between revisions of "Tetration"

From TORI
Jump to navigation Jump to search
m (→‎Applications: misprints)
 
(25 intermediate revisions by the same user not shown)
Line 1: Line 1:
  +
{{top}}
−
[[File:Tetreal10bx10d.png|400px|right|thumb|$y={\rm tet}_b(x)~~$ versus $x$ for various $b$]]
  
  +
<div class="thumb tright" style="float:right; margin:-72px 0px 8px 18px; line-height:11px; width:300px">
−
<!-- [[File:Tet10bxr.png|600px|right|thumb|$y={\rm tet}_b(x)$ versus $x$ for various $b$.]] !-->
  
  +
{{pic|Tetreal10bx10d.png|300px}}<small><center>\(y=\mathrm{tet}_b(x)\) versus \(x\) for various values of base \(b\). &nbsp; [[Суперфункции]]<ref name="ru"/>,с.244,Рис.17.1;&nbsp; [[Superfunctions]]<ref name="en"/>,p.239,Fig.17.2.</center></small>
−
<!--
  
  +
</div>
−
[[File:Tetreal2215.jpg|400px|thumb|$f={\rm tet}_b(x)$ in the $x,b~$ plane shown with levels $f= \rm const$.]] !-->
  
  +
<div class="thumb tright" style="float:right; background-color:#fff; margin:2px 0px 8px 8px; width:300px; line-height:9px">
−
[[File:Ackerplot.jpg|400px|thumb|Tetration to base e (dashed) compared to other [[Ackermann function]]s]]
  
  +
{{pic|Ackerplot.jpg|300px}}<small><center>First five [[ackermann]]s. [[Superfunctions]]<ref name="en">
−
'''Tetration''' (or Tetrational) ${\rm tet}_b$ to base $b \in \mathbb R$, $b\!>1$<br>
  
  +
https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862<br>
−
is the $\mathbb C \mapsto \mathbb C$ function, which is solution of equations
  
  +
https://mizugadro.mydns.jp/BOOK/468.pdf
−
: ${\rm tet}_b(z\!+\!1) = \exp_b\!\big( {\rm tet}_b(z) \big)$
  
  +
Dmitrii Kouznetsov. Superfunctions. [[Lambert Academic Publishing]], 2020.
−
: ${\rm tet}_b(0) = 1$
  
  +
</ref>,p.266,Fig.19.7.</center></small>
−
such that, at least for $b\!>\!1$, is holomorphic at least in $\{ z \in \mathbb C : \Re(z)\!>\!-2\}$.
 
  +
</div>
  +
<div class="thumb tright" style="float:right; margin:8px 0px 14px 12px; background-color:#fff; width:220px; line-height:11px;">
  +
{{pic|B271t.png|240px}}<small><center>Map of [[natural tetration]]. [[Superfunctions]]<ref name="en"/>,p.203,Fig.4.12 </center></small>
  +
</div>
  +
[[Tetration]] ([[Тетрация]]) is the [[superfunction]] of the [[exponential]] map.
  +
For a given base \(b\), the tetration \(\operatorname{tet}_b\) is defined as the function satisfying the transfer equation
  +
\[
  +
\operatorname{tet}_b(z+1) = b^{\operatorname{tet}_b(z)}
  +
\]
  +
together with additional normalization and regularity conditions that select a unique solution among infinitely many possible superfunctions.
  +
For real values of the argunet, the explicit plots of \(\operatorname{tet}_b(x)\) versos \(x\)
  +
for various real values of base \(b\) is shown in figure at right.
   
  +
The inverse function [[ArcTetration]] is denoted with symbol ate; \( \mathrm{ate}_b = \mathrm{tet}_b^{-1} \).<br>
−
Parameter $b$ is called "base", as in the cases of [[exponential]] and [[logarithm]]. According to the first of equations above, $\mathrm{tet}_b$ is [[superfunction]] of [[exponential]] to base $b$. Exponential is [[transfer function]] of tetration.
  
  +
The iterates of [[Exponential]] can be expressed as follows:
  +
\(
  +
\exp_b^{\ n}=\operatorname{tet}_b\big(n+\operatorname{ate}_b(z)\big)
  +
\).
  +
Here, number \(n\) of the iterate has no need to be integer. In particular, \(\varphi=\exp^{1/2}\)
  +
appears as solution of equation \( \varphi(\varphi(x))=\mathrm e^x \); this equation had been considered by [[Hellmuth Kneser]] <ref name="k">
  +
http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi
  +
[[Hellmuth Kneser]]. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen.
  +
Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67
  +
</ref>, 1950.
   
  +
==Notations==
−
For real $b$, it is assumed that ${\rm tet}_b(z^*)={\rm tet}_b(z)^*$, where the asterisk means the complex conjugation. For the case of base $b \!=\! \mathrm e$, the index may be omitted (as in the case of exp and logarithm), id est, ${\rm tet}(z)={\rm tet}_{\rm e}(z)$. The solution is believed to exist and to be unique, although not all mathematicians agree that the proof of the existence and the uniqueness is rigorous.
  
   
  +
The name [[tetration]] reflects its role as the next operation after exponentiation within the [[hyperoperation]] hierarchy:<br>
−
Case of complex values of $b$ is under investigation; conditions, that make the solution of equations above unique, may have need to be reformulated.
  
  +
[[Ackermann]]\(_1\), id est, the [[Addition]] appears as [[superfunction]] of [[unity increment]];<br>
  +
[[Ackermann]]\(_2\), id est, the [[Multiplication]] appears as [[superfunction]] of additon; <br>
  +
[[Ackermann]]\(_3\), id est, the [[Exponential]] \(\exp\) appears as [[superfunction]] of multiplication;<br>
  +
[[Ackermann]]\(_4\), id est, the [[Tetration]] \(\mathrm{tet}\) appears as [[superfunction]] of [[exponential]];<br>
  +
[[Ackermann]]\(_5\), id est, the [[Pentation]] \(\mathrm{pen}\) appears as [[superfunction]] of [[tetration]];<br>
  +
and so on. These functions are qualified as [[ackermann]]s after the last name of
  +
mathematician [[Wilhelm Ackermann]].
   
  +
The most studied case is the [[Natural tetration]]
−
==Tetration as superfunction==
  
  +
<ref name="analuxp">
−
The tetration is [[superfunction]] of the [[exponential]]. The tetration can be interpreted as iterated exponential applied to unity. In the language [[Mathematica]], there already exists the special notation for the superfunction, id est, the function '''Nest'''. In particular,
 
  +
https://www.ams.org/journals/mcom/2009-78-267/S0025-5718-09-02188-7/home.html <br>
−
${\rm tet}(z)={\rm Nest}[\exp,1,z]$ .
 
−
Up to year 2011, '''Nest''' is implemented only for the integer values of the last argument; the use with any expression, different from an integer constant, causes the error message.
  
−  
−
For the beginning of year 2011, the tetration has been analyzed mainly for the real values of base $b \! > \! 1$.
  
−
The different algorithms are used for the evaluation at
 
−  
−
$1 \! < \! b \! < \! \exp(1/\rm e)$
 
−
<ref name="sqrt2">
  
−
http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html <br>
  
−
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf <br>
  
 
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf
  
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf
  +
Dmitrii Kouznetsov. Solution of F⁡(z+1)=exp⁡(F⁡(z)) in complex z-plane.
−
D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
  
  +
Mathematics of Computation, 2009, V.78, p.1647-1670.
−
</ref>,
  
  +
</ref><ref name="vladi">
  +
https://mizugadro.mydns.jp/PAPERS/2010vladie.pdf<br>
  +
https://www.vmj.ru/articles/2010_2_4.pdf <br>
  +
https://mizugadro.mydns.jp/PAPERS/2010_2_4.pdf
  +
D.Kouznetsov. Tetration as special function. (In Rusian) [[Vladikavkaz Mathematical Journal]], 2010, v.12, issue 2, p.31-45.
  +
</ref>. It corresponds to base \(b=\mathrm e\); it can be written simply as
  +
\[
  +
\operatorname{tet}(z)=\operatorname{tet}_{\mathrm e}(z).
  +
\]
  +
For base \(\mathrm e\) the first five [[ackermann]]s are shown in figure at right.<br>
  +
The dashed line refers to the [[natural tetration]].
   
  +
In such a way, all the [[ackermann]]s are numerated. <br>
−
$b \! = \! \exp(1/\rm e)\approx 1.44$
 
  +
In notation [[Ackermann]]\(_m (z)\), the number \(m\) is supposed to be positive integer (natural number). <br>
−
<ref name="e1e">
  
  +
To year 2025, the generalization of [[Ackermann]]\(_m(z)\) for non-integer values of \(m\) is not yet developed.
−
http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf <br>
  
  +
However, the argument \(z\) may have complex values.
−
http://www.ils.uec.ac.jp/~dima/PAPERS/2011e1e.pdf H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). [[Mathematics of computation]],
 
−
2012 February 8. ISSN 1088-6842(e) ISSN 0025-5718(p)
  
−
</ref>,
  
   
  +
[[Complex map]]s of [[tetration]] to various bases are shown in figures below.
−
and for
 
  +
Lines \(u=\mathrm{const} \) and
−
$b \! >\! \exp(1/\rm e)$
 
  +
lines \(v=\mathrm{const} \) are drawn for \(u+\mathrm i v=\mathrm{tet}_b(x\!+\!\mathrm i y)\).
−
<ref name="moc1">
  
−
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html D.Kouznetsov. (2009). Solutions of $F(z+1)=\exp(F(z))$ in the complex plane.. Mathematics of Computation, 78: 1647-1670. DOI:10.1090/S0025-5718-09-02188-7. </ref><ref name="vladi">
  
−
http://www.ils.uec.ac.jp/~dima/PAPERS/2010vladie.pdf
  
−
D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
 
−
</ref><ref name="aeq">
 
−
http://www.springerlink.com/content/u7327836m2850246/
  
−
H.Trappmann, D.Kouznetsov. Uniqueness of Analytic Abel Functions in Absence of a Real Fixed Point. Aequationes Mathematicae, v.81, p.65-76 (2011)</ref>.
  
   
  +
==Definition==
−
Therefore, one could expect some peculiarity of ${\rm tet}_b(z)$ at
 
−
$b\!=\!\exp(1/\rm e)$.
 
   
  +
Let \(T_b(z)=b^z\).
−
On the other hand, the plots of this function look smooth; one might expect that at a fixed value of $z$, ${\rm tet}_b(z)$ is [[holomorphic]] (analytic) with respect to $b$, and, in particular, in vicinity of $b \! \approx \! \exp(1/\rm e)$. However, the visual smoothness at the real values of $b$ can substitute neither the investigation of the analytic properties for complex $b$ nor the mathematical proof of [[holomorphizm]].
  
  +
A function \(F\) is a ''[[superexponential]]'' (a [[superfunction]] of \(T_b\)) if
  +
\[
  +
F(z+1) = T_b(F(z)).
  +
\]
   
  +
A [[tetration]] to real base \(b\) is real-holomorphic superexponential \(F\)
−
==Behavior at $1\!<\!b\!<\exp(1/{\rm e})$==
  
  +
such that \(F(x+\mathrm i y)\) remains bounded at \(y\to\pm\infty\) and \(F(0)=1\).
−
At $1\!<\!b\!<\exp(1/{\rm e})$, tetration is [[superfunction]] constructed with [[regular iteration]] at smallest of the real [[fixed point]]s $L\!=\!L_1$, $L\!=\!L_2$ of $\log_b$.
 
−
In language [[Mathematica]], the value of the fixed point can be expressed with function ProductLog,
  
−
: $L_1(b)=-(\mathrm{ProductLog}[- \mathrm{Log}[b]]/\mathrm{Log}[b])$.
  
   
  +
Such a solution is believed to exists and to be unique <ref>
−
The tetration is [[periodic function]]; the period
  
  +
https://link.springer.com/article/10.1007/s00010-010-0021-6
−
: $T=\frac{2\pi \mathrm i} {\ln(L \, \ln(b))} $
  
  +
https://mizugadro.mydns.jp/2011uniabel.pdf
−
is pure imaginary. The cut line $\{x \in \mathbb R: x\le -2\}$ is reproduced at the translations along the imaginary axis.
 
  +
H.Trappmann, D.Kouznetsov. Uniqueness of holomorphic Abel functions at a complex fixed point pair.
  +
[[Aequationes Mathematicae]], v.81, p.65-76 (2011)
  +
</ref><ref>
  +
https://math.stackexchange.com/questions/284868/uniqueness-of-tetration
  +
Let 𝑓(0)=1
  +
and 𝑓(𝑥+1)=2^𝑓(𝑥) //
  +
Also let f be infinitely differentiable. Then does f exist and is it unique? //
  +
If f is merely continuous, then any continuous function such that f(0)=1 f(1)=2 satisfies the conditions(if f is defined in [0,1] ,we can use the property to define it everywhere else). Similar things can be said for differentiability. But I don't how to solve the problem if it's infinitely differentiable.
  +
</ref>.
   
  +
==Special cases==
−
$\mathrm{tet}_b(x)$ remains real at $x>-2$. It has logarithmic singularity at $x=-2$, and it is [[monotonous function}monotonous]]ly grows at
  
  +
<div class="thumb tright" style="float:right; margin:-6px 0px 4px 8px; background-color:#fff; width:480px; line-height:8px;">
−
$x>-2$.
  
  +
{{pic|E1efig09abc1a150.png|480px}}<small><center>[[Complex map]]s of [[tetration]] \(\mathrm{tet}_b\) to base \(b\!=\!1.5\) , left; \(b\!=\!\exp(1/\mathrm e)\) , center ; \(b\!=\!\sqrt{2}\) , right. [[Суперфункции]]<ref name="ru"/>,с.251,Рис.17.4; [[Superfunctions]]<ref name="en"/>,p.245,Fig.17.4;
  +
</center></small>
  +
</div>
  +
<div class="thumb tright" style="float:right; margin:4px 0px 8px 8px; width:480px;">
  +
{{pic|Tetsheldonmap03.png|480px}}<small><center>[[Tetration to Sheldon base]].
  +
[[Суперфункции]]<ref name="ru"/>,с.257,Рис.18.3; [[Superfunctions]]<ref name="en"/>,p.250, top of Fig.18.3.</center></small>
  +
</div>
   
  +
[[Decimal tetration]], \(b=10\). The routine for the evaluation is loaded as [[F4ten.cin]].
−
The tetration approaches its fixed point $L_1=L_1(b)$ at large values of the real part of its argument (and, in particular, along the real axis).
  
  +
It is used to plot the top picture.
   
  +
[[Natural tetration]], \(b=\mathrm e\). The [[complex map]] for this case is shown in figure above. The original description <ref name="analuxp"/> and the fast C++ implementation <ref name="vladi"/> are published and mentioned in book [[Superfunctions]] <ref name="en"/>
−
==Evaluation and behavior at $b\!=\! \exp(1/{\rm e})$==
  
   
  +
[[Binary tetration]], \(b=2\), see [[Base 2]]
−
For base $b\!=\!\exp(1/{\rm e})\! \approx\! 1.44$, the standard [[regular iteration]] should be modified.
  
   
  +
[[tetration to base 1.5]], see [[Base 1.5]]
−
In partucular, the "new expansion"
  
−
<ref name="e1e">e1e</ref> is suggested:
  
−
: $\displaystyle
  
−
F(z)=\mathrm e\cdot\left(1-\frac{2}{z}\left(
  
−
1+\sum_{m=1}^{M} \frac{P_{m}\big(-\ln(\pm z) \big)}{(3z)^m}
 
−
+\mathcal{O}\!\left(\frac{|\ln(z)|^{m+1}}{z^{m+1}}\right)
  
−
\right) \right) $
  
−
where
  
−
: $\displaystyle P_{m}(t)=\sum_{n=0}^{m} ~c_{n,m~}~ t^n$
  
−
The substitution of into equation $~ F(z\!+\!1)\!=\!\exp(F(z)/\mathrm e)~$
  
−
and the asymptotic analysis with small parameter $|1/z|$ determines
  
−
the coefficients $c$ in the polynomials above. In particular,
 
−
: $ \begin{array}{ccc}
  
−
P_{1}(t)&=&t \\
  
−
P_{2}(t)&=&t^{2}+t+1/2 \\
  
−
P_{3}(t)&=&t^{3}+\frac{ 5}{ 2}t^{2}+\frac{ 5}{2}t +\frac{ 7}{10} \\
  
−
P_{4}(t)&=&t^{4}+\frac{13}{ 3}t^{3}+\frac{ 45}{6}t^{2}+\frac{53}{10}t +\frac{ 67}{60} \\
  
−
P_{5}(t)&=&t^{5}+\frac{77}{12}t^{4}+\frac{101}{6}t^{3}+\frac{83}{ 4}t^{2}+\frac{653}{60}t+\frac{2701}{1680}
  
−
\end{array} $
  
−
The evaluation with 9 polynomials $P$ gives an approximation of $\tilde F(z)$ with 15 decimal digits at $\Re(z)\!>\!4$.
  
−
For small values of $z$, the iterations of formula $F(z)=\ln(F(z\!+\!1))\!~ \mathrm e$
  
−
can be used.
 
   
  +
[[Crytical tetration]], \(b= \mathrm e^{1/\mathrm e}\), see [[Base e1e]]
−
The tetration can be approximated as
  
−
: $\mathrm{tet}_{\exp(1/\mathrm{e})}(z)= F(x_0\!+\!z)$
  
−
where $x_0$ is solution of equation $F(x_0)=1$.
  
−
With the [[complex double]] precision, the resulting approximation returns of order of 14 correct decimal digits in the whole complex plane
  
−
(except the singularities).
  
   
  +
[[Tetration to base sqrt2]], \(b= \sqrt{2}\), see [[Base sqrt2]]
−
The tetration is aperiodic, holomorphic in the range $\mathbb C \backslash \{ x\in \mathbb R : x\!\le\! -2 \}$.
  
−
A large values of the argument, it approaches the limiting value $\mathrm e$, independently on the direction.
  
−
In particular, along the real axis, the the function shows the monotonic growth from $-\infty$ at $-2$ to $\mathrm e$ at infinity, passing through points (-1,0) and (0,1).
  
   
  +
[[Tetration to Sheldon base]] \(b=1.52598338517+0.0178411853321\ \mathrm i\).
−
At any $z$ from the range of definition, In vicinity of $b\!\approx\!\exp(1/\mathrm e)$, tetration $\mathrm{tet}_b(z)$ seems to be continuous function of $b$, although very different agorithms are used for the evaluation in the three cases,
 
  +
The original algorithm <ref name="analuxp"/> allows the straight-forward generalization for the case of complex values of base \(b\). After the request by [[Sheldon Levenstain]], the complex map of this [[tetration]] had been generated; it is shown in figure at right.
−
$1\!<\!b\!<\!\exp(1/\mathrm e)$,
  
−
$b=\exp(1/\mathrm e)$, and
  
−
$b\!>\!\exp(1/\mathrm e)$. The figure below collects the [[complex map]]s of tetration to base
 
−
$b\!=\!1.5$ , left,
 
−
$b\!=\!\exp(1/\mathrm e)$ , center, and
  
−
$b\!=\!\sqrt{2}$ , right. $f\!=\! \mathrm{tet}_b(x\!+\!\mathrm i y)$ is shown in the $x,y$ plane with levels
  
−
$~p\!=\!\Re(f)\!=\! \mathrm{const}~$ and levels
  
−
$~q\!=\!\Im(f)\!=\! \mathrm{const}~$. The integer values correspond to the thick lines.
  
−
[[File:E1efig09abc1a150.png|1200px|left|thumb|[[Complex map]]s of $\mathrm{tet}_{b}$ for $b\!=\! 1.5$, $\exp(1/\mathrm e)$ , $\sqrt{2}$; $p\!+\!\mathrm i q=\mathrm{tet}_b(x\!+\!\mathrm i y)$]]
  
   
−
==Behavior at $b\!\approx\! \exp(1/{\rm e})$, $z\!\approx\! 0$==
 +
==Continuity at base b=exp(1/e)==
  +
<div class="thumb tright" style="float:right; margin:0 0 8px 8px; width:280px; line-height:10px">
−
If the ${\mathrm{tet}}_b(z)$ is holomorphic in some vicinity of $b\!\approx \! \exp(1/{\rm e})$, $z\!\approx 0$, then it is expandable into the Taylor series
  
  +
{{pic|BlackSheep.png|280px}}
−
:$\displaystyle
  
  +
<small><center>"half-sheep". [[Суперфункции]]<ref name="ru">
−
{\mathrm {tet}}_b(x)=1+\sum_{n=1}^{N-1} \!
  
  +
https://mizugadro.mydns.jp/BOOK/202.pdf
−
\left(\sum_{m=0}^{M-1} \!
  
  +
Дмитрий Кузнецов. [[Суперфункции]]. [[Lambert Academic Publishing]], 2014
−
c_{m,n} \beta^m +
  
  +
</ref>,с.218,Рис.15.6; [[Superfunctions]] <ref name="en"/>,p.215,Fig.15.6</center></small>
−
O(\beta^M)
  
  +
</div>
−
\right) x^n
 
−
+{\mathcal O}(x^N)
  
−
$
  
−
where
 
−
$\beta = b\!-\! \exp(1/\mathrm e)$; the coefficients $c$ of this expansion can be estimated fitting the evaluations of tetration, using the algorithms reported for real base. This leads to the following preliminary estimates:
 
−
:$
  
−
\begin{array}{ccrrrrrr}
  
−
m&c_{m,0} &c_{m,1} ~ ~ ~& c_{m,2} ~ ~ ~ & c_{m,3} ~ ~ ~ &c_{m,4}~ ~ ~ \\
  
−
0 & 1 & 0.61061 &-0.23171 & 0.09225 &-0.03757\\
  
−
1 & 0 & 0.69521 & 0.41315 &-0.16027& 0.07007 \\
  
−
2 & 0 &-0.57851 & 0.18323 & 0.49162&-0.15216 \\
  
−
3 & 0 & 0.64730 &-0.62933 &-0.51128& 0.51372\\
  
−
4 & 0 &-0.84098 & 1.23261 & 0.42470&-0.97551 \\
  
−
5 & 0 & 1.19090 &-2.12653 &-0.06895& 1.57684
 
−
\end{array}
  
−
$
  
−
However, the precision of such evaluation is not so high (perhaps, only two or three decimal digits are significant in the estimates above); for the efficient evaluation of the coefficients of such an expansion, the tetration to the complex base should be analyzed. Such an analysis could be matter for the further research. Any independent confirmation (or correction) of the approximations of the coefficients above should be appreciated.
  
   
  +
This cartoon at right illustrates a philosophical point in tetration theory:<br>
−
==Behavior at $b\!>\!\exp(1/\mathrm e)\!\approx 1.44$==
  
  +
<b>"The only we may conclude, that in this county, there is at least one sheep,
  +
and at least the right-hand side of this animal is black"</b>. <br>
  +
The heuristic assumptions that appear “obvious’’ (e.g., that the right side of a sheep has the same color as its left side) appears without rigorous proof and, from point of a mathematician, may happen to be wrong.
   
  +
The similar heuristic assumption refers to the continuity of [[tetration]] \(\mathrm{tet}_b(z) \) being considered as function of base \(b\) at point \(b=\exp(1/\mathrm e)\).
−
Tetration is holomorphic in the whole complex plane except part of the real axis $\{ x\in \mathbb R : x\le -2 \}$.
  
−
As the real part of the argument goes to $-\infty$, the tetration exponentially approaches the fixed point $L$ at the upper halfplane and $L^*$ at the lower halfplane, although has [[countable set]] of weak singularities along the cut line $\{ x\in \mathbb R : x\le -2 \}$.
  
−
As the real part of the argument grows, the tetration shows complicated, [[fractal]]-like structures. In the [[complex map]], the lines of zero real part are reproduced at the unity translations along the real axis, but the new and new details appear at each step.
  
   
  +
The maps above for \(b=1.5\), \(b=\exp(1/\mathrm e)\approx 1.44\) and \(b=\sqrt{2}\approx 1.41\)
−
== Case $b\!=\! \mathrm{e}$==
  
  +
as well as the explicit plot at the top make an impression, that the [[tetration]] is continuous and perhaps holomorphic with respect to \(b\) at this point: the variation in the 3d significant figure causes small change of the view of the curves; at least for moderate valies of argument \(z\)
−
<!--\!=\! \mathrm{e} \!\approx\2.71 !-->
  
   
  +
As in the case of the sheep in the cartoon, this assumptions about tetration
−
[[File:B271t.png|400px|thumb|[[Complex map]] of $\mathrm{tet}$]]
  
  +
is not obvious and require careful justification.
−
The case of [[natural tetration]] refers to base $b\!=\!\mathrm e\! \approx\! 2.71~$; this case is considered in years 2010, 2011
  
−
<ref name="moc2009">
  
−
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670.
  
−
</ref><ref name="vladi">
  
−
http://tori.ils.uec.ac.jp/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
  
−
</ref>. The fast complex(double) implementation in [[C++]] is suggested.
  
   
  +
The preliminary numerical analysis indicates, that
−
As in the case of exponential, in the indication of the natural tetration, the subscript can be omitted:
  
−
$\exp_{\mathrm{e}}=\exp$ and
+
\(\mathrm{tet}_b(z)\) for \(\Re(b)<\exp(1/\mathrm e)\)
  +
is not analytical extension of
−
$\mathrm{tet}_{\mathrm{e}}=\mathrm{tet}$.
  
  +
\(\mathrm{tet}_b(z)\) for \(\Re(b)>\exp(1/\mathrm e)\);
  +
in the simplest way, the cut line along line \(\Re(b)=\exp(1/\mathrm e)\)
  +
divides the complex plane to two almost independent parts,
  +
and only in point \(b=\exp(1/\mathrm e)\), these two [[tetration]]s have the same limiting
  +
[[tetration]]. <br>
  +
However, the cut at the complex \(b\)-plane has no need to follow the vertical line \(\Re(b)=\exp(1/\mathrm e)\); but this choice is simplest and has priority (following the last, 6th of the [[TORI axioms]].)
   
  +
==Applications==
−
The figure shows the [[complex map]] of natural tetration; the real and the imaginary parts of
 
  +
The obvious application of the tetration may refer to representation of huge numbers.<br>
−
$f\!=\!\mathrm {tet}(x+\mathrm i y)$ are shown in the $x$,$y$ plane with levels
 
  +
For example the [[Googolplex]] number <ref>
−
$u\!=\! \Re(f)\!=\! \mathrm {const}$ and
  
  +
https://en.wikipedia.org/wiki/Googolplex
−
$v\!=\! \Im(f)\!=\! \mathrm {const}$.
  
  +
A '''googolplex''' is the [[large number]] \(10^{10^{100}}\), that is, 10 raised to the power of a [[googol]]. If written out in ordinary [[decimal notation]], it would be 1 followed by a [[googol]] (10<sup>100</sup>) zeroes – a physically impossible number to write explicitly.
  +
</ref> can be expressed as follows:
  +
\[
  +
10^{10^{100}}=\mathrm{tet}_{10}^3(2)
  +
\]
  +
However, up to year 2025, Editor have not yet found any [[scientific concept]]
  +
that deals with such a huge number.
   
  +
The more realistic application may refer to the approximation of processes that
−
In the upper half-plane, the tetration approaches the limiting value, which is [[fixed point]] $L$ of natural [[logarithm]]; $L$ is solution of $L\!=\!\ln(L)$, and $L\!\approx\! 0.318132 + 1.33724 \mathrm i$.
  
  +
grows faster than any polynomial but slower than any exponential.
  +
The non-integer iterates greatly extend the arsenal of functions available for
  +
construction of efficient fits, involving less fitting parameters and/or providing better precision and/or having wider range of approximation.
   
  +
The \(n\)-th iterate of the exponential:
−
In the lower half-plane, the tetration approaches the conjugated value, id est, $L^*\!\approx\! 0.318132 - 1.33724 \mathrm i$.
  
  +
\[
  +
\exp_b^{\ n}(z) = \operatorname{tet}_b\!\big(n + \operatorname{ate}_b(z)\big),
  +
\]
  +
for real \(n\). One example of such a function is mentioned in the Preamble.
   
  +
An additional extension could be generalization of [[ackermann]]\(_m\)
−
==Tetration to complex base==
  
  +
to non-integer values of \(m\), looking for the real-holomorphic solition \(A\) of equations
−
[[File:Tetsheldonmap03.png|660px|thumb| $f=\mathrm{tet}_s(x\!+\!\mathrm i y)$ with
 
  +
\[
−
lines $u\!=\!\Re(f)\!=\!\mathrm{const}$
 
  +
A_m(z+1)=A_{m-1}(A_m(z)) \\
−
and $v\!=\!\Im(f)\!=\!\mathrm{const}$]]
  
  +
A_2(z)= \mathrm e\ z \\
−
The method with the Cauchi equation
  
  +
Z_m(0)=1 \text{ for } m>2
−
<ref name="moc1">
  
  +
\]
−
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html D.Kouznetsov. (2009). Solutions of $F(z\!+\!1)=\exp(F(z))$ in the complex plane.. Mathematics of Computation, 78: 1647-1670. DOI:10.1090/S0025-5718-09-02188-7. </ref>
  
  +
treating \(A_m(z)\) as holomorphic function of two variables \(m\) and \(z\).<br>
−
can be used also for the complex values of the base.
 
  +
Such a generalization can be matter for the future research.
−
The following properties should be assumed:
  
−
: $\displaystyle \lim_{y\rightarrow +\infty}$ $\mathrm{tet}_b(x+\mathrm i y)= \mathrm{Filog}(a)$
  
−
: $\displaystyle \lim_{y\rightarrow -\infty}$ $\mathrm{tet}_b(x+\mathrm i y)= \mathrm{Filog}(a^*)^*$
  
−
where $a=\ln(b)$ and [[Filog]] is holomorphic function, $t=\mathrm{filog}(a)$ is solution of equation
  
−
:$ \log_b(f)=f$
  
   
  +
==Acknowledgement==
−
The [[Filog]] function can be expressed through the [[Tania function]] and through the [[WrighOmega]] funciton as follows:
  
   
  +
[[ChatGPT]] helped to improve this article.
−
: $\displaystyle \mathrm{Filog}(z)= \frac{\mathrm{Tania}\!\big(\ln(z)-1-\mathrm{i}\big)}{-z} = \frac{\mathrm{WrightOmega}\!\big(\ln(z)-\mathrm{i}\big)}{-z}$
  
   
−
===Sheldon base===
 +
==References==
  +
{{ref}}
−
The [[complex map]] of
 
−
$\mathrm{tet}_s$ is shown at figure at right, where $s$ is the [[Sheldon base]],
 
−
: $\!\!\!\!\!\!\!\! \!\!\!\!\!\!\!\! s=1.52598338517 + 0.0178411853321~{i}$ .
 
−
See the special article [[Tetration to Sheldon base]] for this case.
  
   
  +
https://en.wikipedia.org/wiki/Ackermann_function
−
The colored plots of various superexponentials for various complex values of base are available at the [[Tetration Fortum]]
  
  +
This function is defined from the [[recurrence relation]] \(\operatorname{A}(m+1, n+1) = \operatorname{A}(m, \operatorname{A}(m+1, n))
−
by [[Sheldon Levenson]]
  
  +
\) with appropriate [[Base case (recursion)|base cases]].
−
<ref name="sheldon">
  
−
http://math.eretrandre.org/tetrationforum/showthread.php?tid=729
  
−
Sheldon Levenson. Complex base tetration program. [[Tetration and Related Topics]], 2012 March 1.
  
−
</ref>; the question wether some of them are tetrations is in discussion.
  
   
  +
https://en.wikipedia.org/wiki/Tetration
−
==Fast growth==
  
  +
In [[mathematics]], '''tetration''' (or '''hyper-4''') is an [[operation (mathematics)|operation]] based on [[iterated]], or repeated, [[exponentiation]]. There is no standard [[mathematical notation|notation]] for tetration, though [[Knuth's up arrow notation]] <math>\uparrow \uparrow</math> and the left-exponent <math>{}^{x}b</math> are common.
−
Along the real axis, the tetration to base $b>\exp(1/\mathrm e)$ shows fast growth; it grows faster than any exponential. Due to such a growth, the tetration could be useful for the [[numerical representation of huge numbers]], that can be stored as $\mathrm {tet}_b(x)$ with moderated values $x$, keeping the stored value of the number distinguishable from $+\infty$. The arithmetics for such "tetrational" variables should be implemented using the properties of the tetration, avoiding the conversion to the conventional floating-point form.
 
   
  +
https://en.citizendium.org/wiki/Tetration
−
Perhaps, at least in century 21, the tetration satisfies the requirements of the [[computational mathematics]] in the rapidly growing functions; if not, the superfunction of tetration, id est, [[pentation]] ($\mathrm {pen}_b$) or even higher [[Ackermann function]]s are available. For natural base ($b\!=\!\mathrm e\!=\!\exp(1) \approx 2.71$), the [[pentation]] $\mathrm{pen}_{\mathrm e}$ can be expressed through the [[regular iteration]], allowing the efficient evaluation while the tetration is already implemented <ref name="vladi">Superexponential as special function</ref>.
  
  +
'''Tetration''' is a rapidly growing [[mathematical function]], which was introduced in the 20th century and proposed for the representation of huge numbers in the Mathematics of Computation. <!--For positive integer values of its argument <math>x</math>, tetration <math>\mathrm{tet}_b(x)</math> on base <math>b</math> can be defined with: <math>{\ \mathrm{tet}_b(x) = \ \atop {\ }} {{\underbrace{b^{b^{\cdot^{\cdot^{b}}}}}} \atop {x}}~</math>
−
<!--
  
−
For the case of natural tetration, the complex double implementations in C++ and than in Mathematica are available at Citizendium; the generators of the figures posted include the codes of the routine used. The details of the implementation are described in the [[Vladikavkaz Mathematical Journal]]
  
 
!-->
  
!-->
   
  +
<small>
−
==Arctetration==
  
  +
https://tetrationforum.org/search.php?action=results&sid=094d9363dba94b4cfc99575883e4e5bb&sortby=&order=desc
−
[[Arctetration]] (ate) is inverse function of tetration; it is [[Abel function]] of the [[exponential]].
  
  +
</small> [[Tetration Forum]]
−
Afctetration $\mathrm {ate}_b$ to base $b$ satisfies the relations
  
−
: $\mathrm{ate}_b(\mathrm{tet}_b(z))=z$
 
−
: $\mathrm{tet}_b(\mathrm{ate}_b(z))=z$
 
−
at least in some ranges of values of $z$. Also, the arctetration satisfies the [[Abel equation]]
  
−
: $\mathrm{ate}_b(b^z)=\mathrm{ate}_b(z) +1$
  
−
Roughly, the arctetration counts, how many times the logarithm should be taken of a value before the value becomes unity.
  
   
  +
https://www.numdam.org/item?id=BSMF_1919__47__161_0
−
While the tetration is [[superfunction]] of the [[exponential]], the arctetration is the [[Abel function]].
  
  +
P. Fatou. Sur les ´equations fonctionnelles. Bulletin de la Soci´et´e
  +
Math´ematique de France, 47 (1919), p. 161-271.
   
  +
https://eretrandre.org/rb/files/Ackermann1928_126.pdf
−
==Iterated exponential==
  
  +
Wilhelm Ackermann. Zum Hilbertschen Aufbau der reellen Zahlen. [[Mathematische Annalen]] 99, Number 1(1928), Z.118-133.
−
The [[superfunction]] and the [[Abel function]] of the exponential are established; they are tetration "tet" and its inverse function "ate".
  
−
Then, the iterated exponential can be expressed as follows:
  
−
: $ \exp_b^c(z)=\mathrm{tet}_b(c+ \mathrm{ate}_b(z))$
  
−
In this expression, the number $c$ of iterations ahs no need to be [[integer number|integer]]; however, at integer values,
  
−
: $\exp_b^{-2}(z)=\log_b(\log_b(z))$
  
−
: $\exp_b^{-1}(z)=\log_b(z)$
  
−
: $\exp_b^{0}(z)= z$
  
−
: $\exp_b^{1}(z)=\exp_b(z)$
  
−
: $\exp_b^{2}(z)=\exp_b(b^z)$ ,
  
−
at least for values of $z$ in some range in vicinity of the real axis; the arctetration unavoidably has the cut lines in the complex plane.
  
   
  +
<small>https://projecteuclid.org/journals/acta-mathematica/volume-100/issue-3-4/Regular-iteration-of-real-and-complex-functions/10.1007/BF02559539.full
−
<!--The representation through the tetration and arctetration allows to evaluate not only integer iterates but even the complex iterates of the exponential.!-->
  
  +
</small>
−
The realizations of the super-exponentials and the Abel–exponential by [[Hellmuth Kneser]]
 
  +
G.Szekeres. Regular iteration of real and complex functions. Acta Mathematica 1958, Volume 100, Issue 3-4, pp 203-258.
−
<ref name="kneser">
  
−
<!--http://www.ils.uec.ac.jp/~dima/Relle.pdf!-->
  
−
http://www.digizeitschriften.de/dms/img/?PPN=GDZPPN002175851
  
−
H.Kneser. Reelle analytische Lösungen der Gleichung $\varphi(\varphi(x))=e^x$.
 
−
Equationes Mathematicae, Journal fur die reine und angewandte Mathematik {\bf 187} 56–67 (1950)</ref>
  
−
also allow to express the non-integer iterate of the exponential, but the functions he had constructed are not real along the real axis. For the applications to the real numbers, at least for base $b\!>\!1$, the representation of iterated exponential through the tetration and arctetration looks more convenient.
  
   
  +
https://www.ams.org/journals/bull/1993-29-02/S0273-0979-1993-00432-4/S0273-0979-1993-00432-4.pdf
−
==Representation of huge numbers==
  
  +
W.Bergweiler. Iteration of meromorphic functions. Bulletin (New Series) of the American Mathematical society, v.29, No.2 (1993) p.151-188.
−
The tetration and the iterated exponential can be used for the representation of huge numbers.
  
−
In partucular the number [[googol]] <ref name="googol">
  
−
http://mathworld.wolfram.com/Googol.html Googol
  
−
</ref> which is $10^{100}$ appears to be $\exp_{10}^2(2) = 10^{10^2}$, while the number [[googolplex]]
  
−
<ref name="googolplex">
  
−
http://mathworld.wolfram.com/Googolplex.html Googolplex
  
−
</ref>
  
−
appears as $\exp_{10}^3(2)=10^{10^{10^2}}$
  
−
==References==
  
−
<references/>
  
   
  +
https://www.tandfonline.com/doi/full/10.1080/10652460500422247
−
http://www.proofwiki.org/wiki/Definition:Tetration <br>
  
  +
M.H.Hooshmand, (2006). Ultra power and ultra exponential functions. Integral [[Transforms and Special Functions]] 17 (8): 549–558
−
http://en.citizendium.org/wiki/Tetrational <br>
  
−
http://en.wikipedia.org/wiki/Tetration<br>
  
−
http://math.eretrandre.org/tetrationforum/index.php <br>
  
−
http://samlib.ru/k/kuznecow_d_j/ackermann.shtml<br>
  
−
http://www.tetration.org/Ackermann/arithmetic.html Daniel Geisler. All is Arithmetic. (2009)
  
−
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 <br>
  
−
http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf <br>
  
−
http://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Press, 2014. In Russian.<br>
  
−
http://mizugadro.mydns.jp/BOOK/441.pdf Dmitrii Kouznetsov. Superfunctions. 2017<br>
  
−
http://myweb.astate.edu/wpaulsen/tetration2.pdf <br>
  
−
http://link.springer.com/article/10.1007/s10444-017-9524-1 <br>
  
−
William Paulsen and Samuel Cowgill.
 
−
Solving $F(z+1)=b^{F (z)}$ in the complex plane.
  
−
Advances in Computational Mathematics, 2017 March 7, p. 1–22
  
   
  +
https://sciencepublishinggroup.com/article/10.11648/j.acm.20140306.14
−
==Keywords==
  
  +
Dmitrii Kouznetsov.
−
[[Arctetration]],
  
  +
Evaluation of Holomorphic Ackermanns.
−
[[Natural tetration]] (to base $b\!=\!e\!\approx \! 2.71$),
  
  +
Published in [[Applied and Computational Mathematics]] (Volume 3, Issue 6)
−
[[Pentation]],
  
  +
Received: 21 November 2014 Accepted: 17 December 2014 Published: 27 December 2014, Page(s) 307-314.
−
[[Superfunction]],
  
−
[[Tetration to Sheldon base]],
  
−
[[Transfer equation]]
  
   
  +
https://www.proquest.com/openview/cb7af40083915e275005ffca4bfd4685/1?pq-origsite=gscholar&cbl=18750
−
[[Суперфункции]]
  
  +
[[Samuel Cowgill]]. EXPLORING TETRATION IN THE COMPLEX PLANE
  +
EXPLORING TETRATION IN THE COMPLEX PLANE
  +
A Thesis presented to the faculty of Arkansas State University in partial.
  +
fulfillment of the requirements for the Degree of
  +
MASTER OF SCIENCE IN MATHEMATICS
  +
ARKANSAS STATE UNIVERSITY //MAY 2017
  +
Approved by:
  +
Dr. [[William Paulsen]], Thesis Advisor
  +
Dr. [[Jie Miao]], Committee Member
  +
Dr. [[Jeongho Ahn]], Committee MemberPREVIE
   
  +
https://link.springer.com/article/10.1007/s10444-018-9615-7
−
[[Category:Book]]
  
  +
William Paulsen. Tetration for complex bases.
−
[[Category:Mathematical functions]]
  
−
[[Category:Mathematics]]
 +
Advances in Computational Mathematics.
  +
Published: 02 June 2018//
−
[[Category:Science]]
  
  +
Volume 45, pages 243–267, (2019)
−
[[Category:Tetration]]
  
−
[[Category:Pentation]]
  
−
[[Category:Superfunctions]]
  
−
[[Category:Articles in English]]
  
   
  +
https://www.researchgate.net/publication/325532999_Tetration_for_complex_bases
−
[[Category:Problem with fig]]
  
  +
<br>
  +
https://www.researchgate.net/figure/Level-curves-for-Rk-b-z-and-Ik-b-z-0-1-2-3-4-for-b-i_fig1_325532999
  +
[[William Harold Paulsen]]. Tetration for complex bases.
  +
Advances in Computational Mathematics 45(6),
  +
February 2019
  +
DOI:10.1007/s10444-018-9615-7
  +
  +
http://myweb.astate.edu/wpaulsen/tetration2.pdf
  +
[[William Paulsen]] and [[Samuel Cowgil]].
  +
Solving F(z+1)=b^F(z) in the complex plane.
  +
  +
{{fer}}
  +
  +
==Keywords==
  +
«[[Abel function]]»,
  +
«[[Ackermann]]»,
  +
«[[ate]]»,
  +
«[[Base e1e]]»,
  +
«[[Base sqrt2]]»,
  +
«[[Exponential]]»,
  +
«[[Filog]]»,
  +
«[[fit1.cin]]»,
  +
«[[Fixed point]]»,
  +
«[[Fsexp.cin]]»,
  +
«[[Fslog.cin]]»,
  +
«[[Hellmuth Kneser]]»,
  +
«[[Iterates]]»,
  +
«[[Iterate of exponential]]»,
  +
«[[Maps of tetration]]»,
  +
«[[Mathematics of Computation]]»,
  +
«[[Logarithm]]»,
  +
«[[Superfunction]]»,
  +
«[[Superfunctions]]»,
  +
«[[tet]]»,
  +
«[[Tetration]]»,
  +
«[[Transfer equation]]»,
  +
  +
[[Category:English]]
  +
[[Category:Exponential]]
  +
[[Category:Superexponential]]
  +
[[Category:Superfunction]]
  +
[[Category:Superfunctions]]
  +
[[Category:Special function]]
  +
[[Category:Tetration]]

Latest revision as of 16:50, 13 December 2025


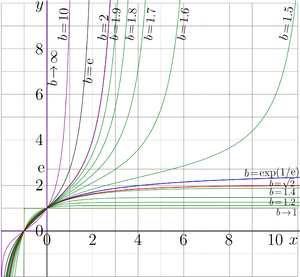
Tetreal10bx10d.png
\(y=\mathrm{tet}_b(x)\) versus \(x\) for various values of base \(b\).   Суперфункции[1],с.244,Рис.17.1;  Superfunctions[2],p.239,Fig.17.2.
Ackerplot.jpg
First five ackermanns. Superfunctions[2],p.266,Fig.19.7.
B271t.png
Map of natural tetration. Superfunctions[2],p.203,Fig.4.12

Tetration (Тетрация) is the superfunction of the exponential map. For a given base \(b\), the tetration \(\operatorname{tet}_b\) is defined as the function satisfying the transfer equation \[ \operatorname{tet}_b(z+1) = b^{\operatorname{tet}_b(z)} \] together with additional normalization and regularity conditions that select a unique solution among infinitely many possible superfunctions. For real values of the argunet, the explicit plots of \(\operatorname{tet}_b(x)\) versos \(x\) for various real values of base \(b\) is shown in figure at right.

The inverse function ArcTetration is denoted with symbol ate; \( \mathrm{ate}_b = \mathrm{tet}_b^{-1} \).
The iterates of Exponential can be expressed as follows: \( \exp_b^{\ n}=\operatorname{tet}_b\big(n+\operatorname{ate}_b(z)\big) \). Here, number \(n\) of the iterate has no need to be integer. In particular, \(\varphi=\exp^{1/2}\) appears as solution of equation \( \varphi(\varphi(x))=\mathrm e^x \); this equation had been considered by Hellmuth Kneser [3], 1950.

Notations

The name tetration reflects its role as the next operation after exponentiation within the hyperoperation hierarchy:
Ackermann\(_1\), id est, the Addition appears as superfunction of unity increment;
Ackermann\(_2\), id est, the Multiplication appears as superfunction of additon;
Ackermann\(_3\), id est, the Exponential \(\exp\) appears as superfunction of multiplication;
Ackermann\(_4\), id est, the Tetration \(\mathrm{tet}\) appears as superfunction of exponential;
Ackermann\(_5\), id est, the Pentation \(\mathrm{pen}\) appears as superfunction of tetration;
and so on. These functions are qualified as ackermanns after the last name of mathematician Wilhelm Ackermann.

The most studied case is the Natural tetration [4][5]. It corresponds to base \(b=\mathrm e\); it can be written simply as \[ \operatorname{tet}(z)=\operatorname{tet}_{\mathrm e}(z). \] For base \(\mathrm e\) the first five ackermanns are shown in figure at right.
The dashed line refers to the natural tetration.

In such a way, all the ackermanns are numerated.
In notation Ackermann\(_m (z)\), the number \(m\) is supposed to be positive integer (natural number).
To year 2025, the generalization of Ackermann\(_m(z)\) for non-integer values of \(m\) is not yet developed. However, the argument \(z\) may have complex values.

Complex maps of tetration to various bases are shown in figures below. Lines \(u=\mathrm{const} \) and lines \(v=\mathrm{const} \) are drawn for \(u+\mathrm i v=\mathrm{tet}_b(x\!+\!\mathrm i y)\).

Definition

Let \(T_b(z)=b^z\). A function \(F\) is a superexponential (a superfunction of \(T_b\)) if \[ F(z+1) = T_b(F(z)). \]

A tetration to real base \(b\) is real-holomorphic superexponential \(F\) such that \(F(x+\mathrm i y)\) remains bounded at \(y\to\pm\infty\) and \(F(0)=1\).

Such a solution is believed to exists and to be unique [6][7].

Special cases

E1efig09abc1a150.png
Complex maps of tetration \(\mathrm{tet}_b\) to base \(b\!=\!1.5\) , left; \(b\!=\!\exp(1/\mathrm e)\) , center ; \(b\!=\!\sqrt{2}\) , right. Суперфункции[1],с.251,Рис.17.4; Superfunctions[2],p.245,Fig.17.4;
Tetsheldonmap03.png
Tetration to Sheldon base. Суперфункции[1],с.257,Рис.18.3; Superfunctions[2],p.250, top of Fig.18.3.

Decimal tetration, \(b=10\). The routine for the evaluation is loaded as F4ten.cin. It is used to plot the top picture.

Natural tetration, \(b=\mathrm e\). The complex map for this case is shown in figure above. The original description [4] and the fast C++ implementation [5] are published and mentioned in book Superfunctions [2]

Binary tetration, \(b=2\), see Base 2

tetration to base 1.5, see Base 1.5

Crytical tetration, \(b= \mathrm e^{1/\mathrm e}\), see Base e1e

Tetration to base sqrt2, \(b= \sqrt{2}\), see Base sqrt2

Tetration to Sheldon base \(b=1.52598338517+0.0178411853321\ \mathrm i\). The original algorithm [4] allows the straight-forward generalization for the case of complex values of base \(b\). After the request by Sheldon Levenstain, the complex map of this tetration had been generated; it is shown in figure at right.

Continuity at base b=exp(1/e)

BlackSheep.png

"half-sheep". Суперфункции[1],с.218,Рис.15.6; Superfunctions [2],p.215,Fig.15.6

This cartoon at right illustrates a philosophical point in tetration theory:
"The only we may conclude, that in this county, there is at least one sheep, and at least the right-hand side of this animal is black".
The heuristic assumptions that appear “obvious’’ (e.g., that the right side of a sheep has the same color as its left side) appears without rigorous proof and, from point of a mathematician, may happen to be wrong.

The similar heuristic assumption refers to the continuity of tetration \(\mathrm{tet}_b(z) \) being considered as function of base \(b\) at point \(b=\exp(1/\mathrm e)\).

The maps above for \(b=1.5\), \(b=\exp(1/\mathrm e)\approx 1.44\) and \(b=\sqrt{2}\approx 1.41\) as well as the explicit plot at the top make an impression, that the tetration is continuous and perhaps holomorphic with respect to \(b\) at this point: the variation in the 3d significant figure causes small change of the view of the curves; at least for moderate valies of argument \(z\)

As in the case of the sheep in the cartoon, this assumptions about tetration is not obvious and require careful justification.

The preliminary numerical analysis indicates, that \(\mathrm{tet}_b(z)\) for \(\Re(b)<\exp(1/\mathrm e)\) is not analytical extension of \(\mathrm{tet}_b(z)\) for \(\Re(b)>\exp(1/\mathrm e)\); in the simplest way, the cut line along line \(\Re(b)=\exp(1/\mathrm e)\) divides the complex plane to two almost independent parts, and only in point \(b=\exp(1/\mathrm e)\), these two tetrations have the same limiting tetration.
However, the cut at the complex \(b\)-plane has no need to follow the vertical line \(\Re(b)=\exp(1/\mathrm e)\); but this choice is simplest and has priority (following the last, 6th of the TORI axioms.)

Applications

The obvious application of the tetration may refer to representation of huge numbers.
For example the Googolplex number [8] can be expressed as follows: \[ 10^{10^{100}}=\mathrm{tet}_{10}^3(2) \] However, up to year 2025, Editor have not yet found any scientific concept that deals with such a huge number.

The more realistic application may refer to the approximation of processes that grows faster than any polynomial but slower than any exponential. The non-integer iterates greatly extend the arsenal of functions available for construction of efficient fits, involving less fitting parameters and/or providing better precision and/or having wider range of approximation.

The \(n\)-th iterate of the exponential: \[ \exp_b^{\ n}(z) = \operatorname{tet}_b\!\big(n + \operatorname{ate}_b(z)\big), \] for real \(n\). One example of such a function is mentioned in the Preamble.

An additional extension could be generalization of ackermann\(_m\) to non-integer values of \(m\), looking for the real-holomorphic solition \(A\) of equations \[ A_m(z+1)=A_{m-1}(A_m(z)) \\ A_2(z)= \mathrm e\ z \\ Z_m(0)=1 \text{ for } m>2 \] treating \(A_m(z)\) as holomorphic function of two variables \(m\) and \(z\).
Such a generalization can be matter for the future research.

Acknowledgement

ChatGPT helped to improve this article.

References

  1. ↑ 1.0 1.1 1.2 1.3 https://mizugadro.mydns.jp/BOOK/202.pdf Дмитрий Кузнецов. Суперфункции. Lambert Academic Publishing, 2014
  2. ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862
    https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.
  3. ↑ http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi Hellmuth Kneser. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen. Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67
  4. ↑ 4.0 4.1 4.2 https://www.ams.org/journals/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
    http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf Dmitrii Kouznetsov. Solution of F⁡(z+1)=exp⁡(F⁡(z)) in complex z-plane. Mathematics of Computation, 2009, V.78, p.1647-1670.
  5. ↑ 5.0 5.1 https://mizugadro.mydns.jp/PAPERS/2010vladie.pdf
    https://www.vmj.ru/articles/2010_2_4.pdf
    https://mizugadro.mydns.jp/PAPERS/2010_2_4.pdf D.Kouznetsov. Tetration as special function. (In Rusian) Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
  6. ↑ https://link.springer.com/article/10.1007/s00010-010-0021-6 https://mizugadro.mydns.jp/2011uniabel.pdf H.Trappmann, D.Kouznetsov. Uniqueness of holomorphic Abel functions at a complex fixed point pair. Aequationes Mathematicae, v.81, p.65-76 (2011)
  7. ↑ https://math.stackexchange.com/questions/284868/uniqueness-of-tetration Let 𝑓(0)=1 and 𝑓(𝑥+1)=2^𝑓(𝑥) // Also let f be infinitely differentiable. Then does f exist and is it unique? // If f is merely continuous, then any continuous function such that f(0)=1 f(1)=2 satisfies the conditions(if f is defined in [0,1] ,we can use the property to define it everywhere else). Similar things can be said for differentiability. But I don't how to solve the problem if it's infinitely differentiable.
  8. ↑ https://en.wikipedia.org/wiki/Googolplex A googolplex is the large number \(10^{10^{100}}\), that is, 10 raised to the power of a googol. If written out in ordinary decimal notation, it would be 1 followed by a googol (10100) zeroes – a physically impossible number to write explicitly.

https://en.wikipedia.org/wiki/Ackermann_function This function is defined from the recurrence relation \(\operatorname{A}(m+1, n+1) = \operatorname{A}(m, \operatorname{A}(m+1, n)) \) with appropriate base cases.

https://en.wikipedia.org/wiki/Tetration In mathematics, tetration (or hyper-4) is an operation based on iterated, or repeated, exponentiation. There is no standard notation for tetration, though Knuth's up arrow notation \(\uparrow \uparrow\) and the left-exponent \({}^{x}b\) are common.

https://en.citizendium.org/wiki/Tetration Tetration is a rapidly growing mathematical function, which was introduced in the 20th century and proposed for the representation of huge numbers in the Mathematics of Computation.

https://tetrationforum.org/search.php?action=results&sid=094d9363dba94b4cfc99575883e4e5bb&sortby=&order=desc Tetration Forum

https://www.numdam.org/item?id=BSMF_1919__47__161_0 P. Fatou. Sur les ´equations fonctionnelles. Bulletin de la Soci´et´e Math´ematique de France, 47 (1919), p. 161-271.

https://eretrandre.org/rb/files/Ackermann1928_126.pdf Wilhelm Ackermann. Zum Hilbertschen Aufbau der reellen Zahlen. Mathematische Annalen 99, Number 1(1928), Z.118-133.

https://projecteuclid.org/journals/acta-mathematica/volume-100/issue-3-4/Regular-iteration-of-real-and-complex-functions/10.1007/BF02559539.full G.Szekeres. Regular iteration of real and complex functions. Acta Mathematica 1958, Volume 100, Issue 3-4, pp 203-258.

https://www.ams.org/journals/bull/1993-29-02/S0273-0979-1993-00432-4/S0273-0979-1993-00432-4.pdf W.Bergweiler. Iteration of meromorphic functions. Bulletin (New Series) of the American Mathematical society, v.29, No.2 (1993) p.151-188.

https://www.tandfonline.com/doi/full/10.1080/10652460500422247 M.H.Hooshmand, (2006). Ultra power and ultra exponential functions. Integral Transforms and Special Functions 17 (8): 549–558

https://sciencepublishinggroup.com/article/10.11648/j.acm.20140306.14 Dmitrii Kouznetsov. Evaluation of Holomorphic Ackermanns. Published in Applied and Computational Mathematics (Volume 3, Issue 6) Received: 21 November 2014 Accepted: 17 December 2014 Published: 27 December 2014, Page(s) 307-314.

https://www.proquest.com/openview/cb7af40083915e275005ffca4bfd4685/1?pq-origsite=gscholar&cbl=18750 Samuel Cowgill. EXPLORING TETRATION IN THE COMPLEX PLANE EXPLORING TETRATION IN THE COMPLEX PLANE A Thesis presented to the faculty of Arkansas State University in partial. fulfillment of the requirements for the Degree of MASTER OF SCIENCE IN MATHEMATICS ARKANSAS STATE UNIVERSITY //MAY 2017 Approved by: Dr. William Paulsen, Thesis Advisor Dr. Jie Miao, Committee Member Dr. Jeongho Ahn, Committee MemberPREVIE

https://link.springer.com/article/10.1007/s10444-018-9615-7 William Paulsen. Tetration for complex bases. Advances in Computational Mathematics. Published: 02 June 2018// Volume 45, pages 243–267, (2019)

https://www.researchgate.net/publication/325532999_Tetration_for_complex_bases
https://www.researchgate.net/figure/Level-curves-for-Rk-b-z-and-Ik-b-z-0-1-2-3-4-for-b-i_fig1_325532999 William Harold Paulsen. Tetration for complex bases. Advances in Computational Mathematics 45(6), February 2019 DOI:10.1007/s10444-018-9615-7

http://myweb.astate.edu/wpaulsen/tetration2.pdf William Paulsen and Samuel Cowgil. Solving F(z+1)=b^F(z) in the complex plane.

Retrieved from "https://mizugadro.mydns.jp/t/index.php?title=Tetration&oldid=46224"