Difference between pages "Main Page" and "Superfunction"
(→Warings) |
|||
| Line 1: | Line 1: | ||
| + | [[Superfunction]] comes from iteration of some function. |
||
| + | For some function <math>T</math> (which is called [[Transfer function]]) and for some constant <math>t</math>, the superfunction \(F\) could be defined with expression |
||
| − | [[TORI]] means '''T'''ools for '''O'''utstanding '''R'''esearch and '''I'''nvestigation. (Russian transliteration: [[ТОРИ]].) |
||
| − | Here, term TORI denotes this site and also the methodology, [[philosophy]] or even [[religion]] used to built-up this site. |
||
| − | <div style="float:right;width:190px"> |
||
| − | [[File:ToriByVika591x744.jpg|200px]] <!-- |200px|thumb|TORI by Vika Mihailovski]] !--> |
||
| − | </div> |
||
| − | ===Meanings=== |
||
| − | Term TORI has many meanings (in addition to the name of site, that collects "Tools for Outstanding Research and Investigation"). Some of them are mentioned in this section. |
||
| + | \(\displaystyle {{F(z)} \atop \,} {= \atop \,} |
||
| − | Tori is nickname of artist [[Viktoria Mikhailovski]]. By her permission, some of her paintings are used to illustrate articles of TORI in the first meaning. |
||
| + | {T^z(t) \atop \,} {= \atop \,} |
||
| + | {{\underbrace{T\Big(T\big(... T(t)...\big)\Big)}} \atop {z \mathrm{~evaluations~of~function~}T\! |
||
| + | \!\!\!\!\!}}\) |
||
| + | then <math>F</math> can be interpreted as superfunction of function <math>T</math>. |
||
| − | Also, Tori ([[User:Tori|鳥]]) is name of first admin of this site (since 2011 to June 2013). |
||
| + | Such definition is valid only for positive integer <math>z</math>. |
||
| − | Some operational systems do not distinguish lower case letters from capital letters; this causes confusions. |
||
| + | The most research and appllications around the superfunctions are related with various extensions of superfunction; and analysis of the existence, uniqueness and ways of the evaluation. |
||
| + | <!-- In particular, :<math>S(1)=f(t)</math> !--> |
||
| + | For simple function <math>T</math>, such as addition of a constant or multiplication by a constant, |
||
| + | the superfunction can be expressed in terms of elementary function. |
||
| + | <!-- |
||
| + | Historically, first non-elementary superfunction considered was super-exponential or [[tetration]], that corresponds to |
||
| + | !--> |
||
| + | In particular, the [[Ackernann functions]] and [[tetration]] can be interpreted in terms of [[superfunction]]s. |
||
| + | <div style="float:right; width:180px"> |
||
| + | <div style="width:190px"> |
||
| + | [[File:HellmuthKneserPhotoNormal.jpeg|190px]]<small> |
||
| + | [[Hellmuth Kneser]], 1958 |
||
| + | <ref> |
||
| + | https://opc.mfo.de/detail?photo_id=7607 On the Photo: Kneser, Hellmuth Location: Oberwolfach Author: Danzer, Ludwig (photos provided by Danzer, Ludwig) Source: L. Danzer, Dortmund Year: 1958 Copyright: L. Danzer, Dortmund Photo ID: 7607 |
||
| + | </ref></small> |
||
| + | </div></div> |
||
| + | ==History== |
||
| − | TORI should not be confused with [[Tory]] which is name of the British Conservative party. |
||
| + | <div style="float:left;width:70px"> |
||
| − | Some automatic grammars to not yet recognize TORI and try to "correct" it to Tory. |
||
| + | <div style="float:right;width:240px"> |
||
| + | [[Image:Sqrt(factorial)LOGOintegralLOGO.jpg|230px]]<small> |
||
| + | logos of Phys. and Math. depts of [[Moscow State University|MSU]]</small> |
||
| + | </div></div> |
||
| + | <div class="thumb tright" style="float:right;width:190px"> |
||
| + | <div style="width:200px"> |
||
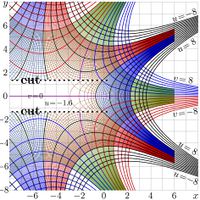
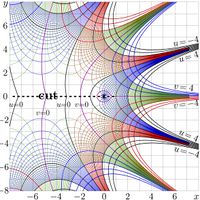
| + | [[File:QexpMapT400.jpg|200px]] \(u+\mathrm i v=\sqrt{\exp} (x+\mathrm i y)\) |
||
| + | [[File:QfacMapT500a.jpg|200px]] \(u+\mathrm i v=\sqrt{!}(x+\mathrm i y)\) |
||
| + | </div></div> |
||
| + | Analysis of superfunctions came from the application to the evaluation of fractional iterations of functions. |
||
| + | |||
| + | [[Superfunction]]s and their inverse functions ([[Abel function]]s) allow evaluation of not only minus-first power of a function (inverse function), but also any real and even complex [[iteration]] of the function. |
||
| + | Historically, the first function of such kind, iteration half of the exponential, id est, |
||
| − | Also, TORI should not be confused with the official site of the [[Institute for Laser Science]], http://www.ils.uec.ac.jp |
||
| + | <math>\sqrt{\exp}~</math>, is considered in 1950 by [[Hellmuth Kneser]] |
||
| + | <ref name="kneser"> |
||
| + | http://tori.ils.uec.ac.jp/PAPERS/Relle.pdf |
||
| + | [[Helmuth Kneser]] |
||
| + | Reelle analytische L¨osungen der Gleichung <math>\varphi(\varphi(x)) = e^x </math> und verwandter Funktionalgleichungen |
||
| + | [[Journal fur die reine und angewandte Mathematik]] '''187''' (1950) 56-67 |
||
| + | </ref>. That time, no algorithm had been suggested for evaluation of this function. |
||
| + | Since 1960, function <math>\sqrt{!~}~</math> is accepted as logo of the Physics department of the [[Moscow State University]], see the first picture of the figure at left. <br> |
||
| − | ===Axioms of TORI=== |
||
| + | Until year 2007, this symbol is believed to have no mathematical sense |
||
| + | <ref name="kandidov"> |
||
| + | V.P.Kandidov. About the time and myself. (In Russian) 2007.05.18. |
||
| + | http://ofvp.phys.msu.ru/pdf/Kandidov_70.pdf: |
||
| + | .. По итогам студенческого голосования победителями оказались значок с изображением |
||
| + | рычага, поднимающего Землю, и нынешний с хорошо известной эмблемой в виде |
||
| + | корня из факториала, вписанными в букву Ф. Этот значок, созданный студентом |
||
| + | кафедры биофизики А.Сарвазяном, привлекал своей простотой и |
||
| + | выразительностью. Тогда эмблема этого значка подверглась жесткой критике со |
||
| + | стороны руководства факультета, поскольку она не имеет физического смысла, |
||
| + | математически абсурдна и идеологически бессодержательна. .. |
||
| + | </ref><ref name="naukai"> |
||
| + | https://www.nkj.ru/archive/articles/1023/ |
||
| + | V.Sadovnichi. 250 anniversary of the Moscow State University. (In Russian) |
||
| + | В. Садовничий. ПЕРВОМУ УНИВЕРСИТЕТУ СТРАНЫ - 250! НАУКА И ЖИЗНЬ, №1, 2005. |
||
| + | .. На значке физфака в букву "Ф" вписано стилизованное изображение корня из факториала (√!) - выражение, математического смысла не имеющее. ..</ref><ref name="logo">Logo of the Physics Department of the Moscow State University. (In Russian); |
||
| + | http://zhurnal.lib.ru/img/g/garik/dubinushka/index.shtml |
||
| + | </ref>. |
||
| + | The [[complex map]]s of functions \( \sqrt{\exp} \) and \(\sqrt{!} \) are shown in figures at right. |
||
| − | TORI is constructed on the base of 6 axioms. Each scientific concept is assumed to have the following properties: |
||
| + | Mathematicians of the same University were not so arrogant and used the symbol of [[integral]] and the [[Moebius surface]] at their logo, see second picture of the figure at left. |
||
| − | '''S1. [[Applicability]]''': The concept has some limited range of validity, distinguishable from the empty set. |
||
| + | That time, researchers did not have computational facilities for evaluation of such functions, but |
||
| − | '''S2. [[Verifiability]]''': In the terms of the already accepted concepts, some specific experiment with some specific result, that confirms the concept, can be described. |
||
| + | the <math>\sqrt{\exp}</math> was more lucky than the <math>~\sqrt{!~}~~</math>; at least the existence of [[holomorphic function]] |
||
| + | <math>\varphi</math> such that <math>\varphi(\varphi(z))=\exp(z)</math> has been declared <ref name="kneser"/>. Actually, for his proof, Kneser had constructed the [[superfunction]] of exp and corresponding [[Abel function]] <math>\mathcal{X}</math>, satisfying the [[Abel equation]] |
||
| + | : <math>\mathcal{X}(\exp(z))=\mathcal{X}(z)+1</math> . |
||
| + | The [[inverse function]], id est <math>F=\mathcal \chi^{-1}</math> is an [[entire function|entire]] super-exponential, although it is not real at the real axis; it cannot be interpreted as [[tetration]], because the condition <math>F(0)=1</math> cannot be realized for the entire super-exponential. The [[real function|real]] <math>\sqrt{\exp}</math> can be constructed with the [[tetration]] (which is also a superexponential), and the real <math>\sqrt{\rm Factorial}</math> can be constructed with the [[SuperFactorial]]. The plots of <math>\sqrt{\rm Factorial}~</math> and <math>\sqrt{\exp}~</math> in the compex plane are shown in the right hand side figure. |
||
| + | ==Extensions== |
||
| − | '''S3. [[Refutability]]''': In the terms of the concept, some specific experiment with some specific result, that negates the concept, can be described. |
||
| + | The recurrent formula of the preamble can be written as equations |
||
| + | \(F(z\!+\!1)=T(F(z)) ~ \forall z\in \mathbb{N} : z>0\) |
||
| − | '''S4. [[Selfconsistency]]''': No internal contradictions of the concept are known. |
||
| + | \(F(1)=t\) |
||
| − | '''S5. [[Principle of correspondence]]''': If the range of validity of a new concept intersects the range of validity of another already accepted concept, then, the new concept either reproduces the results of the old concept, or indicates the way to refute it. (For example, the estimate of the range of validity of the old concept may be wrong.) |
||
| + | Instead of the last equation, one could write |
||
| − | '''S6. [[Pluralism]]''': Mutually-contradictive concepts may coexist; if two concepts satisfying S1-S5 have some common range of validity, then, in this range, the simplest of them has priority. |
||
| + | \(F(0)=t\) |
||
| − | ===Science=== |
||
| + | and extend the range of definition of superfunction <math>F</math> to the non-negative integers. Then, one may postulate |
||
| − | In TORI, the development and analysis of the concepts satisfying the axioms S1-S6 is called [[science]] |
||
| − | <ref> http://pphmj.com/abstract/5076.htm D.Kouznetsov. Support of non-traditional concepts. [[Far East Journal of Mechanical Engineering and Physics]], '''1''', No.1, p.1-6 (2010)</ref><ref> http://ufn.ru/tribune/trib120111 D.Kouznetsov. Place of science and physics in the human knowledge. Physics-Uspekhi, v.181, Трибуна, p.1-9 (2011, in Russian) |
||
| − | </ref><ref name="mestori"> |
||
| − | [[Place of science in the human knowledge]] |
||
| − | </ref>. |
||
| − | The colleagues who accept the axioms above are cordially invited to participate as authors, editors and/or reviewers of TORI.<!-- (Please, verify that your browser understands the formulas in the [[test]] article.) Those who do not accept some of S1-S6 are invited to participate in the [[competing wikis]].!--> |
||
| + | \(F(-1)=T^{-1}(t)\) |
||
| − | More detailed justification of the TORI axioms is suggested in manuscript [[TORI axioms and the application in Physics]] |
||
| + | |||
| − | <ref> |
||
| + | and extend the range of validity to the negative integer values, at least while the inverse of the Transfer function is holomorphic. |
||
| − | https://file.scirp.org/Html/1-7501430_36560.htm<br> |
||
| + | For example, |
||
| − | http://www.ils.uec.ac.jp/~dima/PAPERS/2013jmp.pdf <br> |
||
| + | |||
| − | http://mizugadro.mydns.jp/PAPERS/2013jmp.pdf |
||
| + | \(F(-2)=T^{-2}(t)=T^{-1}\Big(T^{-1}(t)\Big)\) |
||
| − | D.Kouznetsov. TORI axioms and the application in Physics. Journal of Modern Physics, 2013, v 4, 1159-1164 |
||
| + | |||
| + | and so on. However, the inverse function may happen to be not defined for some values of <math>t</math>. |
||
| + | |||
| + | The [[tetration]] is considered as super-function of exponential for some real base <math>b</math>; in this case, |
||
| + | |||
| + | \(T=\exp_{b}\) |
||
| + | |||
| + | then, at \(t=1\), |
||
| + | |||
| + | \(F(-1)=\log_b(1)=0 ~ ~, ~ ~ \mathrm{but}\) |
||
| + | |||
| + | \(F(-2)=\log_b(0)~ \mathrm{~is~ not~ defined}\) |
||
| + | |||
| + | For extension to non-integer values of the argument, superfunction should be defined in different way. |
||
| + | |||
| + | ==Definition== |
||
| + | For complex numbers <math>~p~</math> and <math>~q~</math>, such that <math>~p~</math> belongs to some connected domain <math>D\subseteq \mathbb{C}</math>,<br> |
||
| + | <!-- <math>a \!\mapsto\! b</math> !--> |
||
| + | superfunction (from <math>p \mapsto q</math>) of [[holomorphic function]] <math>~T~</math> on domain <math>C \in \mathbb C</math> is |
||
| + | function <math> F </math>, [[holomorphic]] on domain <math>D</math>, such that |
||
| + | |||
| + | \(F(z\!+\!1)=T(F(z)) ~ \forall z\in D : z\!+\!1 \in D\) |
||
| + | |||
| + | \(F(p)=q\) |
||
| + | |||
| + | ==Uniqueness== |
||
| + | In general, the super-function is not unique. |
||
| + | For a given base function <math>T</math>, from given <math>(p\mapsto q)</math> superfunciton <math>F</math>, another <math>(p \mapsto q)</math> superfunction <math>\tilde F</math> could be constructed as |
||
| + | : <math>\tilde F(z)=F(z+\mu(z))</math> |
||
| + | where <math>\mu</math> is any 1-periodic function, holomorphic at least in some vicinity of the real axis, such that <math> \mu(p)=0 </math>. |
||
| + | |||
| + | The modified superfunction may have narrowed range of holomorphism. |
||
| + | The narrower is the range of holomorphism, the wider is variety of superfunctions allowed <ref name="walker"> |
||
| + | http://www.jstor.org/stable/2938713 |
||
| + | P.Walker |
||
| + | Infinitely differentiable generalized logarithmic and exponential functions |
||
| + | [[Mathematics of computation]], '''196''' (1991), 723-733 |
||
</ref>. |
</ref>. |
||
| − | <!-- |
||
| − | ===Logo=== |
||
| − | The logo at the left upper corner indicates that the function [[square root of factorial]] (that remains symbol of the Physics department of the Moscow State University) first time has been implemented in [[Japan]] <ref>http://www.springerlink.com/content/qt31671237421111/fulltext.pdf?page=1 D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12</ref>. Such a function is an example of that falls into the category of [[science]] determined with the axioms above. |
||
| − | !--> |
||
| + | At large enough range of holomorphism, the super-function is expected to be unique, for each specific |
||
| − | Picture in the left upper corned shows the simpelst formulas about non-integer iterate of exponential.<br> |
||
| + | specific [[transfer function]] <math>T</math>. In particular, the <math>(C, 0\mapsto 1)</math> super-function of |
||
| − | Function \( f=\sqrt{\exp} = \exp^{1/2} \) is iteration half of exponential.<br> |
||
| + | <math>\exp_b</math>, for <math>b>1</math>, is called [[tetration]] and is believed to be unique at least for |
||
| − | Its second iterate gives exponent, \( f^2=\exp \) .<br> |
||
| + | <math>C= \{ z \in \mathbb{C} ~:~\Re(z)>-2 \}</math>; for the case <math> b>\exp(1/\mathrm{e})</math>, see <ref name="kouznetsov"> |
||
| − | In wide range of values \(x\), the relation holds: |
||
| + | http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html |
||
| − | \( f(f(x))=\exp(x) \) |
||
| + | (preprint: http://www.ils.uec.ac.jp/~dima/PAPERS/analuxp99.pdf ) |
||
| + | D.Kouznetsov. |
||
| + | Solutions of <math>F(z+1)=\exp(F(z))</math> in the complex <math>z</math>plane. |
||
| + | [[Mathematics of Computation]], |
||
| + | '''78''' (2009) 1647-1670 |
||
| + | <!--10.1090/S0025-5718-09-02188-7!--> |
||
| + | </ref>. |
||
| + | ==Examples== |
||
| − | More detailed description of these properties, the heneralisation are presented in article |
||
| + | The short version of the [[table of superfunctions]] is suggested in |
||
| − | [[Superfunction]] and in book [[Superfunctions]]. The logo shows an example of that is considered as [[science]] here. |
||
| + | <ref name="superfactorial"> |
||
| + | http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf |
||
| + | D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. [[Moscow University Physics Bulletin]], 2010, v.65, No.1, p.6-12. |
||
| + | </ref>. A little bit more extended table is avilable at [[TORI]] |
||
| + | <ref name="toritable"> |
||
| + | http://tori.ils.uec.ac.jp/TORI/index.php/Table_of_superfunctions |
||
| + | </ref>. |
||
| + | Some superfunctions can be expressed with elementary functions, |
||
| + | they are used without to mention that they are superfunctions. |
||
| + | For example, for the transfer function "++", which means unity increment, |
||
| + | the superfunction is just addition of a constant. |
||
| + | ===Addition=== |
||
| − | Picture in the left upper corned shows the simpelst formulas about non-integer iterate of exponential.<br> |
||
| + | Chose a [[complex number]] <math>c</math> and define function |
||
| − | Function \( f=\sqrt{\exp} = \exp^{1/2} \) is iteration half of exponential.<br> |
||
| + | <math>\mathrm{add}_c</math> with relation |
||
| − | Its second iterate gives exponent, \( f^2=\exp \) .<br> |
||
| + | <math>\mathrm{add}_c(z)=c\!+\!z ~ \forall z \in \mathbb{C}</math> |
||
| − | In wide range of values \(x\), the relation holds: |
||
| + | <!-- , where <math>c\in \mathbb{C}</math> is constant.!-->. |
||
| − | \( f(f(x))=\exp(x) \) |
||
| + | Define function |
||
| − | Description of these properties, the generalisations are presented in article |
||
| + | <math>\mathrm{mul_c}</math> with relation |
||
| − | [[Superfunction]] and in book [[Superfunctions]]. |
||
| + | <math>\mathrm{mul_c}(z)=c\!\cdot\! z ~ \forall z \in \mathbb{C}</math>. |
||
| + | Then, function <math>~\mathrm{mul_c}~</math> is '''superfunction''' (<math>~0</math> to <math>~ c~</math>) |
||
| − | ===Content of TORI=== |
||
| + | of function <math>~\mathrm{add_c}~</math> on <math>~\mathbb{C}~</math>. |
||
| − | The main working language of TORI is English, but the texts may be also in Japanese, in Russian, in Spanish or in other languages. The translations and the links to the translations are welcomed. The texts may be [[science|scientific]], [[religion|religious]] or [[art|artistic]]; |
||
| − | the religious and artistic texts are supposed to be illustrations for scientific texts. Colleagues who want to collaborate, should send their short CV (preferably less than one screen) to the Top Editor, dima(at)ils.uec.ac.jp |
||
| + | ===Multiplication=== |
||
| − | The quality of texts for TORI is estimated by the Main Editor; if possible – on the base of opinions of the voluntary reviewers; so, the post-moderation is assumed. The texts should allow the free distribution; the primary sources (if copypasted from already published articles) should be attributed. The attribution is important to simplify the tracing (and correction) of errors, if any. |
||
| + | Exponentiation <math>\exp_c</math> is superfunction (from 1 to <math>c</math>) of function <math>\mathrm{mul}_c </math>. |
||
| + | ===Quadratic polynomials=== |
||
| − | The main orientation of TORI is [[Science]]; especially [[Mathematics]] and [[Physics]]; other topics may appear as they touch Science. Especially interesting is [[Laser science]], as it deals with one of the most developed applications of [[Quantum mechanics]]. In order see what is it about, one may look at the article [[ILS]]. |
||
| + | Let the transfer funciton \(T\) be defined with \(T(z)=2 z^2-1\). |
||
| + | Then, |
||
| + | \(F(z)=\cos( \pi \cdot 2^z) \) is a |
||
| + | \((\mathbb{C},~ 0\! \rightarrow\! 1)\) superfunction of \(T\). |
||
| + | Indeed, |
||
| − | TORI represent mainly the doubtful concepts; concepts, that stay outside from the main stream of the scientific research; concept that cause discussions. For the official information about our Institute, please, go to the official site http://www.ils.uec.ac.jp |
||
| + | \(F(z\!+\!1)=\cos(2 \pi \cdot 2^z)=2\cos(\pi \cdot 2^z)^2 -1 =T(F(z))\) |
||
| − | Some articles TORI apply not only to Physics, but to othed sciences too. |
||
| − | The declarations of the Russian representatives about [[Katyn-2]] are examples of violation of [[logic]]; the news about the [[Nevsky_Express_bombing_(2009)]] appear as violation of the principle of [[causality]], the claims about [[gravitsapa]] (and other activity of the [[Khrunichev's center]] and, especially, the [[Maximov's institute]]) contradict the law of [[conservation of energy-momentum]]. The [[Fukushima disaster]] appeared because it affects the development of [[TORI]]. However, even in these cases, the 6 axioms above still apply to the concepts suggested (for example, apply to the question [[Who contaminates Japan?]]). Since 2012 the situation about [[Fukushima]] normalized and the main orientation of TORI recovered. |
||
| − | However, some deviations due to, for example, fraud at the [[2011.12.04.Election]] may happen from time to time, the world-wide frauds are analyzed with high priority. The same apply to the statements of some colleagues about [[Skolkovo]]. If someone believe that Skolkovo is scientific center, one may express this point of view, confirming it with links to the results obtained at Skolkovo. |
||
| + | and |
||
| − | The content of TORI may be used for free; however the source should be attributed. It is not for the keeping of the priority, but to simplify the tracing and correction of errors, if any. |
||
| + | \(F(0)=\cos(2\pi)=1\) |
||
| − | ===Criticizm of TORI=== |
||
| − | TORI is not expected to compete with Wikipedia, Citizendium, nor with other [[wiki]]s. Some articles from there are imported to simplify the referencing, but the most of TORI articles are supposed to express some view pretty different from that of other resources. Such a view, according to the axioms above, should be justified. This justification appears as critics. |
||
| + | In this case, the superfunction \(F\) is periodic; its period |
||
| − | No any customs, additional to the 6 axioms declared, are accepted as canonical; all the other statements are considered as refutable concepts and must allow the critics. In this sense, TORI is very critical. |
||
| + | \(\tau=\frac{2\pi}{\ln(2)} \mathrm{i}\approx 9.0647202836543876194 \!~i \) |
||
| − | TORI represents the point of view of the Top Editor, namely Dmitrii Kouznetsov, and not the policy of the [[ILS]]. |
||
| − | Therefore, critics of TORI and the suggestions about the improvement should be send directly to the Editor DmitriiKouznetsov(ɑ)gmail.com . |
||
| + | and the superfunction approaches unity also in the negative direction of the real axis, |
||
| − | If You think, that your point of view is important for the Science, as it is defined above, please express it in a form, suitable for copypasting "as is". Your text may include critics of TORI. |
||
| + | \(\lim_{x\rightarrow -\infty} F(x)=1\) |
||
| − | The content of TORI is compiled on the base of work of many colleagues; and the achievements described in TORI are assumed to be attributed to the Scientific Community. |
||
| − | However, all the mistakes and all the cases of unilateral representation of phenomena and events are just errors of the Editor. The indications of these errors are appreciated; they will be corrected as soon as possible. |
||
| + | The example above and the two examples below are suggested at |
||
| − | The critics of the article in TORI should be expressed either in English, or in the same language, as the main language of the article. Articles in Spanish should be criticized in Spanish, articles in Japanese should be criticized in Japanese, articles in Russian should be criticized in Russian. |
||
| + | <ref name="mueller">Mueller. Problems in Mathematics. http://www.math.tu-berlin.de/~mueller/projects.html </ref> |
||
| − | <!-- However, English is declared as main working language of TORI and may be used to criticize any article.!--> |
||
| + | In general, the transfer function \(T\) has no need to be [[entire function]]. |
||
| − | ===Warings=== |
||
| + | Here is the example with [[meromorphic function]] \(T\). |
||
| + | Let |
||
| + | \(T(z)=\frac{2z}{1-z^2} ~ \forall z\in D~\); \(~ D=\mathbb{C} \backslash \{-1,1\}\) |
||
| − | It you look for some "instanding" concept, then, TORI may be not best place to begin with. You may go to Citizendium, Wikipedia, cyclowiki, etc. <br> |
||
| − | TORI is created for the collection and development of concepts satisfying all the 6 axioms below; such concepts are qualified as [[science|scientific]]. This makes difference between TORI and sites of other "outstanding" philosophies (religious cults, political parties, etc.) |
||
| + | Then, function |
||
| − | TORI represent the point of view of the Editor. |
||
| − | If you disagree with some statements, you should criticize them and suggest your statement, your concept on the topic. <br> |
||
| − | The critics and suggestions can be sent to dmitriiKouznetsov@gmail.com |
||
| + | \(F(z)=\tan(\pi 2^z)\) |
||
| − | Attempts to remove the existing content, instead of to express your point of view, are qualified as [[vandalism]], [[scientific misconduct]], [[censorship]] and elements of [[fascism]] and [[inquisition]]. <!-- |
||
| + | |||
| − | P.S. Sorry, the previous location of TORI, id est <b>tori.ils.uec.ac.jp/TORI</b> had been disabled since 2013 February 27. |
||
| + | is \((C, 0\! \mapsto\! 0)\) superfunction of function \(T\), where |
||
| + | \(C\) is the set of complex numbers except singularities of function \(F\). |
||
| + | For the proof, the trigonometric formula |
||
| + | \(\displaystyle |
||
| + | \tan(2 \alpha)=\frac{2 \tan(\alpha)}{1-\tan(\alpha)^2}~~ |
||
| + | \forall \alpha \in \mathbb{C} \backslash \{\alpha\in \mathbb{C} : \cos(\alpha)=0 || \sin(\alpha)=\pm \cos(\alpha) \} |
||
| + | \) |
||
| + | can be used at <math>\alpha=\pi 2^z </math>, that gives |
||
| + | |||
| + | \(\displaystyle |
||
| + | T(F(z))=\frac{2 \tan(\pi 2^z)}{1-\tan(\pi 2^z)} = \tan(2 \pi 2^z)=F(z+1)\) |
||
| + | <!-- However, such function <math>F(z)</math> allows the holomrphic extension to values, where <math>cos(\pi 2^z)=0</math>, |
||
| + | setting it to zero in these points, but it has singularities, poles, at <math>2^z=\frac{1+2n}{4}</math> for integer <math>n</math>. |
||
!--> |
!--> |
||
| − | === |
+ | ===Algebraic function=== |
| + | In the similar way one can consider the transfer function |
||
| + | |||
| + | \(T(z)=2z \sqrt{1-z^2}\) |
||
| + | |||
| + | and |
||
| + | |||
| + | \(F(z)=\sin(\pi 2^z)\) |
||
| + | |||
| + | which is \((C,~ 0\!\rightarrow \!0)\) superfunction of \(H\) for |
||
| + | \(C= \{z\in \mathbb C : \Re( \cos(\pi 2^z))>0 \}\). |
||
| + | |||
| + | ===Exponentiation=== |
||
| + | Let |
||
| + | <math>b>1</math>, |
||
| + | <math>T(z)= \exp_b(z)</math>, |
||
| + | <math> C= \{ z \in \mathbb{C} : \Re(z)>-2 \}</math>. |
||
| + | Then, [[tetration]] <math> \mathrm{tet}_b </math> |
||
| + | is a <math>(C,~ 0\! \rightarrow\! 1)</math> superfunction of <math>\exp_b</math>. |
||
| + | |||
| + | ==Abel function== |
||
| + | Inverse of superfunction \(G=F^{-1}\) is called the [[Abel function]]; within some domain, it satisfies the Abel equation |
||
| + | |||
| + | \(T(G(z))=G(z)+1\) |
||
| + | |||
| + | ==Applications of superfunctions and the Abel functions== |
||
| + | |||
| + | Superfunctions, usially the [[tetration|superexponential]]s, are proposed as a fast-growing function for an |
||
| + | upgrade of the [[floating point]] representation of numbers in computers. Such an upgrade would greatly extend the |
||
| + | range of huge numbers which are still distinguishable from infinity. |
||
| + | |||
| + | Other applications refer to the calculation of fractional iterates |
||
| + | (or fractional power) of a function. Any holomorphic function can be declared as a "transfer function", then its superfunctions and |
||
| + | corresponding Abel functions can be considered. |
||
| + | ===Nest=== |
||
| + | The \(c\)th iteration of some function \(f\) can be expressed through the [[superfunction]] \(F\) and the [[Abel function]] \(G=F^{-1}\): |
||
| + | :\( T^c(z)=F(c+G(z))\) |
||
| + | In [[Mathematica]], there already exist the special name for the operation, that could evaluate such a expression. It is called [[Nest]]. |
||
| + | <ref name="nest"> |
||
| + | http://reference.wolfram.com/mathematica/ref/Nest.html |
||
| + | </ref>. This function has 3 arguments. |
||
| + | The first argument indicates the name of the function. |
||
| + | The second argument indicates the initial value. |
||
| + | The third (and last) argument indicates the number of iterations. |
||
| + | Then, the iteration of function \(T\) can be written as follows: |
||
| + | :\( T^c(z)=\mathrm {Nest}[T,z,c]\) |
||
| + | |||
| + | Unfortunately, in the version "Mathematica 8", the implementation of the [[Nest]] has serious restrictions: the number of iterations should allow the simplification to an integer constant. |
||
| + | The intents to call function [[Nest]] with any other expression as the last argument cause the error messages. One may hope, in the future versions of Mathematica this bug will be corrected. |
||
| + | |||
| + | The [[Table of superfunctions|table of known superfunctions]] and the corresponding [[Abel function]]s |
||
| + | (similar to that suggested in <ref name="superfactorial"> |
||
| + | http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf |
||
| + | D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. [[Moscow University Physics Bulletin]], 2010, v.65, No.1, p.6-12. |
||
| + | </ref>) |
||
| + | could be loaded in Mathematica in a manned similar to that the [[table of integrals]] is loaded. This would allow the correct implementation of [[Nest]] for the case of non–integer number of iterations. |
||
| + | |||
| + | ===Transition from a function to its inverse function=== |
||
| + | [[Image:Expc.jpg|200px|left|thumb|<math>\exp^c(x)</math> versus <math>x</math> for various <math>c</math>]] |
||
| + | [[Image:Sqrt(exp)(z).jpg|600px|right|thumb|<math>\exp^c</math> in the complex plane for various <math>c</math>]] |
||
| + | |||
| + | A [[superfunction]] <math>S</math> allows to calculate the fractional [[iteration]] <math>H^c</math> of some transfer function <math>H</math>. Once the superfunction <math>S</math> and the [[Abel function]] <math>A=S^{-1}</math> are established, |
||
| + | the fractional iteration can be defined as |
||
| + | <math>H^c(z)=S(c+A(z))</math>. Then, as <math>c</math> changes from 1 to <math>-1</math>, the holomorphic transition from function <math>H</math> to <math>H^{-1}</math> is relalised. The figure at left shows an example of transition from |
||
| + | <math>\exp^{1}\!=\!\exp </math> to |
||
| + | <math>\exp^{\!-1}\!=\!\ln </math>. |
||
| + | Function <math>\exp^c</math> versus real argument is plotted for |
||
| + | <math>c=2,1,0.9, 0.5, 0.1, -0.1,-0.5, -0.9, -1,-2</math>. The [[tetration]]al and ArcTetrational were used as superfunction |
||
| + | <math>F</math> |
||
| + | and Abel function <math>G</math> of the exponential. |
||
| + | The figure at right shows these functions in the [[complex plane]]. |
||
| + | At non-negative integer number of [[iteration]], the iterated exponential is [[entire function]]; at non-integer values, it has two [[branch points]], thich correspond to the [[fixed points]] <math>L</math> and |
||
| + | <math>L^*</math> of natural logarithm. At <math>c\!\ge\! 0</math>, function <math>\exp^c(z)</math> remains [[holomorphic function|holomorphic]] at least in the strip <math>|\Im(z)|<\Im(L)\approx 1.3 </math> along the real axis. |
||
| + | |||
| + | ===Nonlinear Optics=== |
||
| + | In the investigation of the nonlinear response of optical materials, |
||
| + | the sample is supposed to be optically thin, in such a way, |
||
| + | that the intensity of the light does not change much as it goes through. |
||
| + | Then one can consider, for example, the absorption as function of the intensity. |
||
| + | However, at small variation of the intensity in the sample, |
||
| + | the precision of measurement of the absorption as function of intensity is not good. |
||
| + | The reconstruction of the superfunction from the Transfer Function allows to work with |
||
| + | relatively thick samples, improving the precision of measurements. In particular, the |
||
| + | Transfer Function of the similar sample, which is half thiner, |
||
| + | could be interpreted as the square root (id est, half-iteration) of the Transfer Function of the initial sample. |
||
| + | |||
| + | Similar example is suggested for a nonlinear optical fiber |
||
| + | <ref name="kouznetsov"> |
||
| + | http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html |
||
| + | (preprint: http://www.ils.uec.ac.jp/~dima/PAPERS/analuxp99.pdf ) |
||
| + | D.Kouznetsov. |
||
| + | Solutions of <math>F(z+1)=\exp(F(z))</math> in the complex <math>z</math>plane. |
||
| + | [[Mathematics of Computation]], |
||
| + | '''78''' (2009) 1647-1670 |
||
| + | <!--10.1090/S0025-5718-09-02188-7!--> |
||
| + | </ref>. |
||
| + | In particular, the [[Tania function]] can be evaluated using the [[Doya function]] and the [[regular iteration]] |
||
| + | <ref name="2013or"> |
||
| + | http://link.springer.com/article/10.1007/s10043-013-0058-6 |
||
| + | Dmitrii Kouznetsov. Superfunctions for amplifiers. Optical Review, July 2013, Volume 20, Issue 4, pp 321-326. |
||
| + | Preprint: http://mizugadro.mydns.jp/PAPERS/2013orSuper.pdf |
||
| + | </ref><!--<ref name="sinapo"> http://mizugadro.mydns.jp/PAPERS/2011singapo.pdf |
||
| + | D.Kouznetsov. Transfer function of an amplifier and characterization of Materials. Singapore, 2011. (slideshow)</ref>!--> |
||
| + | at the fixed point \(0\), as \(\mathrm{Doya}_t(0)\!=\!0\). The same method can be applied also to other [[transfer funciton]]s, even if they cannot be easy represented through the [[special function]]s. This may refer, for example, to the experimentally–measured transfer function, that has no need to coincide with the [[Doya function]]. |
||
| + | |||
| + | ===Nonlinear Acoustics=== |
||
| + | It may have sense to characterize the nonlinearities in the |
||
| + | attenuation of shock waves in a homogeneous tube. This could find an application in some |
||
| + | advanced muffler, using nonlinear acoustic effects to withdraw the energy of the sound waves |
||
| + | without to disturb the flux of the gas. Again, the analysis of the nonlinear response, |
||
| + | id est, the Transfer Function, |
||
| + | may be boosted with the superfunction. |
||
| + | |||
| + | ===Vaporization and condensation=== |
||
| + | <!--For the separation of isotopes due to the different pressure of the saturated vapor for different components,!--> |
||
| + | In analysis of condensation, the growth (or vaporization) of a small drop of liquid can be considered, |
||
| + | as it diffuses down through a tube with some uniform concentration of vapor. |
||
| + | In the first approximation, at fixed concentration of the vapor, |
||
| + | the mass of the drop at the output end can be interpreted as the |
||
| + | Transfer Function of the input mass. |
||
| + | The square root of this Transfer Function will characterize the tube of half length. |
||
| + | |||
| + | ===Snow avalanche=== |
||
| + | The mass of a snowball, that rolls down from the hill, |
||
| + | can be considered as a function of the path it already have passed. At fixed length of this path |
||
| + | (that can be determined by the altitude of the hill) this mass can be considered also as a Transfer Function of the input mass. The mass of the snowball could be measured at the top of the hill and at thе bottom, giving the Transfer Function; then, the mass of the snowball as a function of the length it passed is superfunction. |
||
| + | |||
| + | ===Operational element=== |
||
| + | If one needs to build-up an operational element with some given transfer function <math>H</math>, |
||
| + | and wants to realize it as a sequential connection of a couple of identical operational elements, then, each of these two elements should have transfer function |
||
| + | <math> h=\sqrt{T}</math>. Such a function can be evaluated through the superfunction and the Abel function of the transfer function <math>T</math>. |
||
| + | |||
| + | The operational element may have any origin: it can be realized as an electronic microchip, |
||
| + | or a mechanical couple of curvilinear grains), or some asymmetric U-tube filled with different liquids, and so on. |
||
| + | |||
| + | ==References== |
||
<references/> |
<references/> |
||
==Keywords== |
==Keywords== |
||
| − | [[ |
+ | [[Abel function]], |
| − | [[ |
+ | [[Iteration]], |
| − | [[ |
+ | [[Regular iteration]], |
| − | [[ |
+ | [[SuperFactorial]], |
| − | [[ |
+ | [[Superfunctions]], |
| + | [[Transfer function]], |
||
| + | [[Transfer equation]], |
||
| + | [[Tetration]], |
||
| + | [[Tania function]], |
||
| + | [[Tania function]], |
||
| + | [[Shoka function]], |
||
| + | [[SuZex]], |
||
| + | [[SuTra]] |
||
| + | |||
| + | [[Суперфункции]] |
||
| + | |||
| + | ===Additional links=== |
||
| + | |||
| + | http://www.proofwiki.org/wiki/Definition:Superfunction |
||
| + | http://en.citizendium.org/wiki/Superfunction |
||
| − | [[Аксиомы ТОРИ]], |
||
| − | [[Наука]], |
||
| − | [[Научный факт]], |
||
| − | [[ТОРИ]] |
||
| − | [[Category:English]] |
+ | [[Category:Articles in English]] |
| − | [[Category: |
+ | [[Category:Iterate]] |
| − | [[Category: |
+ | [[Category:Iteration]] |
| − | [[Category: |
+ | [[Category:Mathematics]] |
| − | [[Category: |
+ | [[Category:Superfunction]] |
Revision as of 19:26, 14 June 2020
Superfunction comes from iteration of some function.
For some function \(T\) (which is called Transfer function) and for some constant \(t\), the superfunction \(F\) could be defined with expression
\(\displaystyle {{F(z)} \atop \,} {= \atop \,} {T^z(t) \atop \,} {= \atop \,} {{\underbrace{T\Big(T\big(... T(t)...\big)\Big)}} \atop {z \mathrm{~evaluations~of~function~}T\! \!\!\!\!\!}}\)
then \(F\) can be interpreted as superfunction of function \(T\). Such definition is valid only for positive integer \(z\). The most research and appllications around the superfunctions are related with various extensions of superfunction; and analysis of the existence, uniqueness and ways of the evaluation. For simple function \(T\), such as addition of a constant or multiplication by a constant, the superfunction can be expressed in terms of elementary function. In particular, the Ackernann functions and tetration can be interpreted in terms of superfunctions.
 Hellmuth Kneser, 1958
[1]
Hellmuth Kneser, 1958
[1]
Contents
History
 logos of Phys. and Math. depts of MSU
logos of Phys. and Math. depts of MSU
Analysis of superfunctions came from the application to the evaluation of fractional iterations of functions.
Superfunctions and their inverse functions (Abel functions) allow evaluation of not only minus-first power of a function (inverse function), but also any real and even complex iteration of the function.
Historically, the first function of such kind, iteration half of the exponential, id est, \(\sqrt{\exp}~\), is considered in 1950 by Hellmuth Kneser [2]. That time, no algorithm had been suggested for evaluation of this function.
Since 1960, function \(\sqrt{!~}~\) is accepted as logo of the Physics department of the Moscow State University, see the first picture of the figure at left.
Until year 2007, this symbol is believed to have no mathematical sense
[3][4][5].
The complex maps of functions \( \sqrt{\exp} \) and \(\sqrt{!} \) are shown in figures at right.
Mathematicians of the same University were not so arrogant and used the symbol of integral and the Moebius surface at their logo, see second picture of the figure at left.
That time, researchers did not have computational facilities for evaluation of such functions, but the \(\sqrt{\exp}\) was more lucky than the \(~\sqrt{!~}~~\); at least the existence of holomorphic function \(\varphi\) such that \(\varphi(\varphi(z))=\exp(z)\) has been declared [2]. Actually, for his proof, Kneser had constructed the superfunction of exp and corresponding Abel function \(\mathcal{X}\), satisfying the Abel equation \[\mathcal{X}(\exp(z))=\mathcal{X}(z)+1\] . The inverse function, id est \(F=\mathcal \chi^{-1}\) is an entire super-exponential, although it is not real at the real axis; it cannot be interpreted as tetration, because the condition \(F(0)=1\) cannot be realized for the entire super-exponential. The real \(\sqrt{\exp}\) can be constructed with the tetration (which is also a superexponential), and the real \(\sqrt{\rm Factorial}\) can be constructed with the SuperFactorial. The plots of \(\sqrt{\rm Factorial}~\) and \(\sqrt{\exp}~\) in the compex plane are shown in the right hand side figure.
Extensions
The recurrent formula of the preamble can be written as equations
\(F(z\!+\!1)=T(F(z)) ~ \forall z\in \mathbb{N} : z>0\)
\(F(1)=t\)
Instead of the last equation, one could write
\(F(0)=t\)
and extend the range of definition of superfunction \(F\) to the non-negative integers. Then, one may postulate
\(F(-1)=T^{-1}(t)\)
and extend the range of validity to the negative integer values, at least while the inverse of the Transfer function is holomorphic. For example,
\(F(-2)=T^{-2}(t)=T^{-1}\Big(T^{-1}(t)\Big)\)
and so on. However, the inverse function may happen to be not defined for some values of \(t\).
The tetration is considered as super-function of exponential for some real base \(b\); in this case,
\(T=\exp_{b}\)
then, at \(t=1\),
\(F(-1)=\log_b(1)=0 ~ ~, ~ ~ \mathrm{but}\)
\(F(-2)=\log_b(0)~ \mathrm{~is~ not~ defined}\)
For extension to non-integer values of the argument, superfunction should be defined in different way.
Definition
For complex numbers \(~p~\) and \(~q~\), such that \(~p~\) belongs to some connected domain \(D\subseteq \mathbb{C}\),
superfunction (from \(p \mapsto q\)) of holomorphic function \(~T~\) on domain \(C \in \mathbb C\) is
function \( F \), holomorphic on domain \(D\), such that
\(F(z\!+\!1)=T(F(z)) ~ \forall z\in D : z\!+\!1 \in D\)
\(F(p)=q\)
Uniqueness
In general, the super-function is not unique. For a given base function \(T\), from given \((p\mapsto q)\) superfunciton \(F\), another \((p \mapsto q)\) superfunction \(\tilde F\) could be constructed as \[\tilde F(z)=F(z+\mu(z))\] where \(\mu\) is any 1-periodic function, holomorphic at least in some vicinity of the real axis, such that \( \mu(p)=0 \).
The modified superfunction may have narrowed range of holomorphism. The narrower is the range of holomorphism, the wider is variety of superfunctions allowed [6].
At large enough range of holomorphism, the super-function is expected to be unique, for each specific specific transfer function \(T\). In particular, the \((C, 0\mapsto 1)\) super-function of \(\exp_b\), for \(b>1\), is called tetration and is believed to be unique at least for \(C= \{ z \in \mathbb{C} ~:~\Re(z)>-2 \}\); for the case \( b>\exp(1/\mathrm{e})\), see [7].
Examples
The short version of the table of superfunctions is suggested in [8]. A little bit more extended table is avilable at TORI [9]. Some superfunctions can be expressed with elementary functions, they are used without to mention that they are superfunctions. For example, for the transfer function "++", which means unity increment, the superfunction is just addition of a constant.
Addition
Chose a complex number \(c\) and define function \(\mathrm{add}_c\) with relation \(\mathrm{add}_c(z)=c\!+\!z ~ \forall z \in \mathbb{C}\) . Define function \(\mathrm{mul_c}\) with relation \(\mathrm{mul_c}(z)=c\!\cdot\! z ~ \forall z \in \mathbb{C}\).
Then, function \(~\mathrm{mul_c}~\) is superfunction (\(~0\) to \(~ c~\)) of function \(~\mathrm{add_c}~\) on \(~\mathbb{C}~\).
Multiplication
Exponentiation \(\exp_c\) is superfunction (from 1 to \(c\)) of function \(\mathrm{mul}_c \).
Quadratic polynomials
Let the transfer funciton \(T\) be defined with \(T(z)=2 z^2-1\). Then, \(F(z)=\cos( \pi \cdot 2^z) \) is a \((\mathbb{C},~ 0\! \rightarrow\! 1)\) superfunction of \(T\).
Indeed,
\(F(z\!+\!1)=\cos(2 \pi \cdot 2^z)=2\cos(\pi \cdot 2^z)^2 -1 =T(F(z))\)
and
\(F(0)=\cos(2\pi)=1\)
In this case, the superfunction \(F\) is periodic; its period
\(\tau=\frac{2\pi}{\ln(2)} \mathrm{i}\approx 9.0647202836543876194 \!~i \)
and the superfunction approaches unity also in the negative direction of the real axis,
\(\lim_{x\rightarrow -\infty} F(x)=1\)
The example above and the two examples below are suggested at [10]
In general, the transfer function \(T\) has no need to be entire function. Here is the example with meromorphic function \(T\). Let
\(T(z)=\frac{2z}{1-z^2} ~ \forall z\in D~\); \(~ D=\mathbb{C} \backslash \{-1,1\}\)
Then, function
\(F(z)=\tan(\pi 2^z)\)
is \((C, 0\! \mapsto\! 0)\) superfunction of function \(T\), where \(C\) is the set of complex numbers except singularities of function \(F\). For the proof, the trigonometric formula \(\displaystyle \tan(2 \alpha)=\frac{2 \tan(\alpha)}{1-\tan(\alpha)^2}~~ \forall \alpha \in \mathbb{C} \backslash \{\alpha\in \mathbb{C} : \cos(\alpha)=0 || \sin(\alpha)=\pm \cos(\alpha) \} \) can be used at \(\alpha=\pi 2^z \), that gives
\(\displaystyle T(F(z))=\frac{2 \tan(\pi 2^z)}{1-\tan(\pi 2^z)} = \tan(2 \pi 2^z)=F(z+1)\)
Algebraic function
In the similar way one can consider the transfer function
\(T(z)=2z \sqrt{1-z^2}\)
and
\(F(z)=\sin(\pi 2^z)\)
which is \((C,~ 0\!\rightarrow \!0)\) superfunction of \(H\) for \(C= \{z\in \mathbb C : \Re( \cos(\pi 2^z))>0 \}\).
Exponentiation
Let \(b>1\), \(T(z)= \exp_b(z)\), \( C= \{ z \in \mathbb{C} : \Re(z)>-2 \}\). Then, tetration \( \mathrm{tet}_b \) is a \((C,~ 0\! \rightarrow\! 1)\) superfunction of \(\exp_b\).
Abel function
Inverse of superfunction \(G=F^{-1}\) is called the Abel function; within some domain, it satisfies the Abel equation
\(T(G(z))=G(z)+1\)
Applications of superfunctions and the Abel functions
Superfunctions, usially the superexponentials, are proposed as a fast-growing function for an upgrade of the floating point representation of numbers in computers. Such an upgrade would greatly extend the range of huge numbers which are still distinguishable from infinity.
Other applications refer to the calculation of fractional iterates (or fractional power) of a function. Any holomorphic function can be declared as a "transfer function", then its superfunctions and corresponding Abel functions can be considered.
Nest
The \(c\)th iteration of some function \(f\) can be expressed through the superfunction \(F\) and the Abel function \(G=F^{-1}\):
- \( T^c(z)=F(c+G(z))\)
In Mathematica, there already exist the special name for the operation, that could evaluate such a expression. It is called Nest. [11]. This function has 3 arguments. The first argument indicates the name of the function. The second argument indicates the initial value. The third (and last) argument indicates the number of iterations. Then, the iteration of function \(T\) can be written as follows:
- \( T^c(z)=\mathrm {Nest}[T,z,c]\)
Unfortunately, in the version "Mathematica 8", the implementation of the Nest has serious restrictions: the number of iterations should allow the simplification to an integer constant. The intents to call function Nest with any other expression as the last argument cause the error messages. One may hope, in the future versions of Mathematica this bug will be corrected.
The table of known superfunctions and the corresponding Abel functions (similar to that suggested in [8]) could be loaded in Mathematica in a manned similar to that the table of integrals is loaded. This would allow the correct implementation of Nest for the case of non–integer number of iterations.
Transition from a function to its inverse function
A superfunction \(S\) allows to calculate the fractional iteration \(H^c\) of some transfer function \(H\). Once the superfunction \(S\) and the Abel function \(A=S^{-1}\) are established, the fractional iteration can be defined as \(H^c(z)=S(c+A(z))\). Then, as \(c\) changes from 1 to \(-1\), the holomorphic transition from function \(H\) to \(H^{-1}\) is relalised. The figure at left shows an example of transition from \(\exp^{1}\!=\!\exp \) to \(\exp^{\!-1}\!=\!\ln \). Function \(\exp^c\) versus real argument is plotted for \(c=2,1,0.9, 0.5, 0.1, -0.1,-0.5, -0.9, -1,-2\). The tetrational and ArcTetrational were used as superfunction \(F\) and Abel function \(G\) of the exponential. The figure at right shows these functions in the complex plane. At non-negative integer number of iteration, the iterated exponential is entire function; at non-integer values, it has two branch points, thich correspond to the fixed points \(L\) and \(L^*\) of natural logarithm. At \(c\!\ge\! 0\), function \(\exp^c(z)\) remains holomorphic at least in the strip \(|\Im(z)|<\Im(L)\approx 1.3 \) along the real axis.
Nonlinear Optics
In the investigation of the nonlinear response of optical materials, the sample is supposed to be optically thin, in such a way, that the intensity of the light does not change much as it goes through. Then one can consider, for example, the absorption as function of the intensity. However, at small variation of the intensity in the sample, the precision of measurement of the absorption as function of intensity is not good. The reconstruction of the superfunction from the Transfer Function allows to work with relatively thick samples, improving the precision of measurements. In particular, the Transfer Function of the similar sample, which is half thiner, could be interpreted as the square root (id est, half-iteration) of the Transfer Function of the initial sample.
Similar example is suggested for a nonlinear optical fiber [7]. In particular, the Tania function can be evaluated using the Doya function and the regular iteration [12] at the fixed point \(0\), as \(\mathrm{Doya}_t(0)\!=\!0\). The same method can be applied also to other transfer funcitons, even if they cannot be easy represented through the special functions. This may refer, for example, to the experimentally–measured transfer function, that has no need to coincide with the Doya function.
Nonlinear Acoustics
It may have sense to characterize the nonlinearities in the attenuation of shock waves in a homogeneous tube. This could find an application in some advanced muffler, using nonlinear acoustic effects to withdraw the energy of the sound waves without to disturb the flux of the gas. Again, the analysis of the nonlinear response, id est, the Transfer Function, may be boosted with the superfunction.
Vaporization and condensation
In analysis of condensation, the growth (or vaporization) of a small drop of liquid can be considered, as it diffuses down through a tube with some uniform concentration of vapor. In the first approximation, at fixed concentration of the vapor, the mass of the drop at the output end can be interpreted as the Transfer Function of the input mass. The square root of this Transfer Function will characterize the tube of half length.
Snow avalanche
The mass of a snowball, that rolls down from the hill, can be considered as a function of the path it already have passed. At fixed length of this path (that can be determined by the altitude of the hill) this mass can be considered also as a Transfer Function of the input mass. The mass of the snowball could be measured at the top of the hill and at thе bottom, giving the Transfer Function; then, the mass of the snowball as a function of the length it passed is superfunction.
Operational element
If one needs to build-up an operational element with some given transfer function \(H\), and wants to realize it as a sequential connection of a couple of identical operational elements, then, each of these two elements should have transfer function \( h=\sqrt{T}\). Such a function can be evaluated through the superfunction and the Abel function of the transfer function \(T\).
The operational element may have any origin: it can be realized as an electronic microchip, or a mechanical couple of curvilinear grains), or some asymmetric U-tube filled with different liquids, and so on.
References
- ↑ https://opc.mfo.de/detail?photo_id=7607 On the Photo: Kneser, Hellmuth Location: Oberwolfach Author: Danzer, Ludwig (photos provided by Danzer, Ludwig) Source: L. Danzer, Dortmund Year: 1958 Copyright: L. Danzer, Dortmund Photo ID: 7607
- ↑ 2.0 2.1 http://tori.ils.uec.ac.jp/PAPERS/Relle.pdf Helmuth Kneser Reelle analytische L¨osungen der Gleichung \(\varphi(\varphi(x)) = e^x \) und verwandter Funktionalgleichungen Journal fur die reine und angewandte Mathematik 187 (1950) 56-67
- ↑ V.P.Kandidov. About the time and myself. (In Russian) 2007.05.18. http://ofvp.phys.msu.ru/pdf/Kandidov_70.pdf: .. По итогам студенческого голосования победителями оказались значок с изображением рычага, поднимающего Землю, и нынешний с хорошо известной эмблемой в виде корня из факториала, вписанными в букву Ф. Этот значок, созданный студентом кафедры биофизики А.Сарвазяном, привлекал своей простотой и выразительностью. Тогда эмблема этого значка подверглась жесткой критике со стороны руководства факультета, поскольку она не имеет физического смысла, математически абсурдна и идеологически бессодержательна. ..
- ↑ https://www.nkj.ru/archive/articles/1023/ V.Sadovnichi. 250 anniversary of the Moscow State University. (In Russian) В. Садовничий. ПЕРВОМУ УНИВЕРСИТЕТУ СТРАНЫ - 250! НАУКА И ЖИЗНЬ, №1, 2005. .. На значке физфака в букву "Ф" вписано стилизованное изображение корня из факториала (√!) - выражение, математического смысла не имеющее. ..
- ↑ Logo of the Physics Department of the Moscow State University. (In Russian); http://zhurnal.lib.ru/img/g/garik/dubinushka/index.shtml
- ↑ http://www.jstor.org/stable/2938713 P.Walker Infinitely differentiable generalized logarithmic and exponential functions Mathematics of computation, 196 (1991), 723-733
- ↑ 7.0 7.1 http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html (preprint: http://www.ils.uec.ac.jp/~dima/PAPERS/analuxp99.pdf ) D.Kouznetsov. Solutions of \(F(z+1)=\exp(F(z))\) in the complex \(z\)plane. Mathematics of Computation, 78 (2009) 1647-1670
- ↑ 8.0 8.1 http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12.
- ↑ http://tori.ils.uec.ac.jp/TORI/index.php/Table_of_superfunctions
- ↑ Mueller. Problems in Mathematics. http://www.math.tu-berlin.de/~mueller/projects.html
- ↑ http://reference.wolfram.com/mathematica/ref/Nest.html
- ↑ http://link.springer.com/article/10.1007/s10043-013-0058-6 Dmitrii Kouznetsov. Superfunctions for amplifiers. Optical Review, July 2013, Volume 20, Issue 4, pp 321-326. Preprint: http://mizugadro.mydns.jp/PAPERS/2013orSuper.pdf
Keywords
Abel function, Iteration, Regular iteration, SuperFactorial, Superfunctions, Transfer function, Transfer equation, Tetration, Tania function, Tania function, Shoka function, SuZex, SuTra