Conjecture on superfunctions
Conjecture on superfunctions (Конжекция о суперфункциях) is hypothesis, concept about application of superfunctions in physics and other sciences.
Two conjectures are formulated below.
Conjecture 1
WIth methods described in articles [3][4][5][6][7][8][9][2], for any physically-meaningful transfer function \(T\), I can construct the physically-meaningful superfunction \(F\), satisfying the transfer equation \(F(z\!+\!1)=T(F(z))\).
Conjecture 2
Let there be some physical dependence denoted with function \(\Phi\).
Let there is a set of experimental data as a table of values of the argument and corresponding values of the function, and also estimates of the error of the measurement.
Let the function \(\Phi\) is assumed to be smooth (real holomorphic), but no physical model to describe its shape is available.
Let there is at least one approximation of function \(\Phi\) in terms of special functions, that are built-in at the programming languages available for year 2003,
that fits the experimental data with satisfactory precision (id est, gives so many correct decimal digits, as the data have),
and Let this fit uses \(M\) adjusting parameters, and let \(~M\!>\!10~\).
Then, with use of superfunctions and the non-integer iterates, I can reduce the number of fitting parameters, keeping the same error of fitting,
or/and reduce the norm of deviation of the fit from experimental data, keeping the same number \(M\) of the fitting parameters.
Example
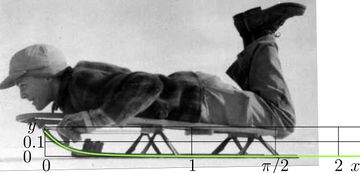
Use of superfunctions and the resulting non-integer iterates greatly extends the arsenal of functions available for fitting of any physical dependences. One may expect, that use of superfunctions allow to improve the approximation (and extrapolation) of various data. In more specific form (to satisfy the TORI axioms), this expectation is formulated as The figure at right illustrates fitting of the shape of the sledge runner with the 100th iteration of sin with single parameter; superfunction and abelfunction of sin can be used to evaluate the iteration.
This article presents the first attempt to formulate the expectation about this applicability as refutable conjectures, as a concept, that satisfies the TORI axioms.
Copyleft 2013 by Dmitrii Kouznetsov.
Keywords
Abel function, Exotic iteration Iteration, Philosophy, Regular iteration, Religion, Superfunction, TORI, TORI axioms,
References
- ↑ http://en.wikipedia.org/wiki/File:Boy_on_snow_sled,_1945.jpg Father of JGKlein. Boy on snow sled, 1945.
- ↑ 2.0 2.1 http://mizugadro.mydns.jp/PAPERS/2014susin.pdf Dmitrii Kouznetsov. Super sin. December 17, 2013. Iterates of function sin are considered. The superfunction SuSin is constructed as holomorphic solution of the transfer equation sin(SuSin(z))=SuSin(z+1). The Abel function AuSin is constructed as solution of the Abel equation AuSin(sin(z))=AuSin(z)+1; in wide range of values z, the rela- tion SuSin(AuSin(z))=z holds. Iteration of sin is expressed with sinˆn(z)=SuSin(n+AuSin(z)), where the number n of iteration has no need to be integer. ..
- ↑
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf
D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670. - ↑
http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
http://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf
http://mizugadro.mydns.jp/PAPERS/2010q2.pdf
D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756. - ↑ http://mizugadro.mydns.jp/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
- ↑
http://www.springerlink.com/content/qt31671237421111/fulltext.pdf?page=1
http://mizugadro.mydns.jp/PAPERS/2010superfae.pdf
D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12. (Russian version: p.8-14) - ↑
http://www.springerlink.com/content/u712vtp4122544x4
http://mizugadro.mydns.jp/PAPERS/2010logistie.pdf
D.Kouznetsov. Holomorphic extension of the logistic sequence. Moscow University Physics Bulletin, 2010, No.2, p.91-98. (Russian version: p.24-31) - ↑
http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf
http://mizugadro.mydns.jp/PAPERS/2012e1eMcom2590.pdf
http://mizugadro.mydns.jp/PAPERS/2011e1e.pdf
H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). Mathematics of Computation. Math. Comp., v.81 (2012), p. 2207-2227. ISSN 1088-6842(e) ISSN 0025-5718(p) - ↑
http://www.m-hikari.com/ams/ams-2013/ams-129-132-2013/kouznetsovAMS129-132-2013.pdf
http://mizugadro.mydns.jp/PAPERS/2013hikari.pdf
D.Kouznetsov. Entire function with logarithmic asymptotic. Applied Mathematical Sciences, 2013, v.7, No.131, p.6527-6541.